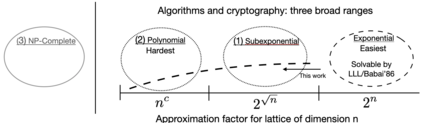
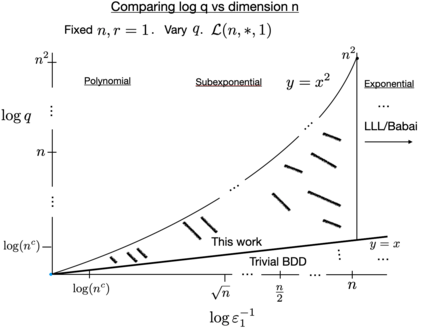
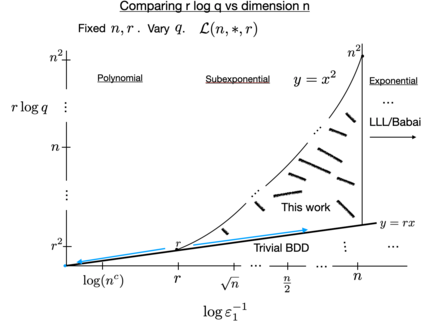
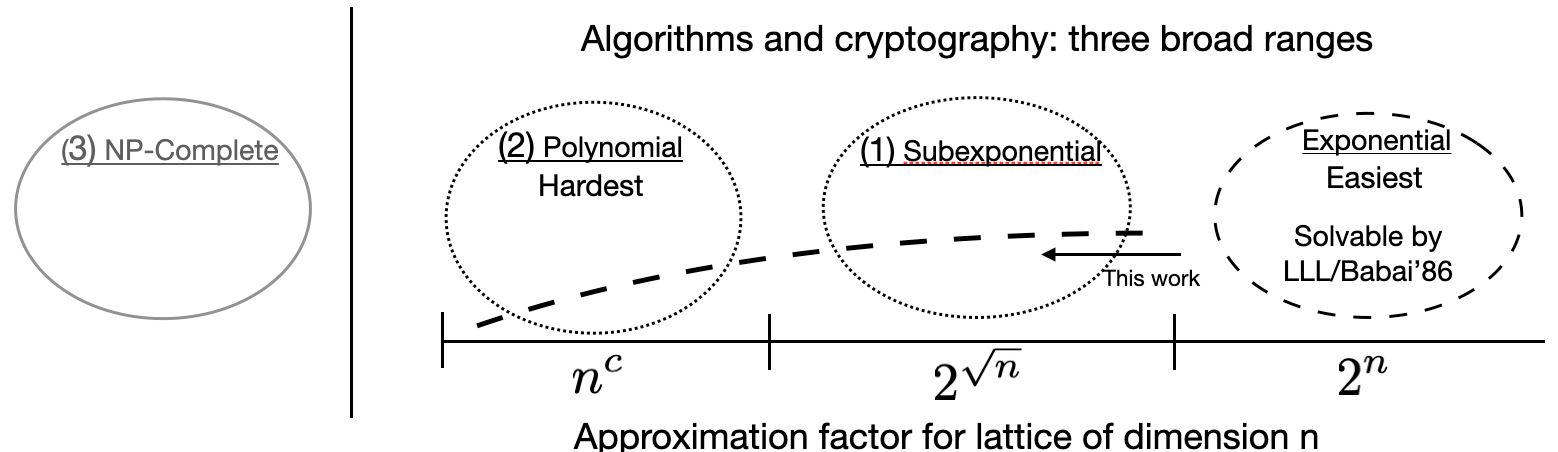
We give a quantum algorithm for solving the Bounded Distance Decoding (BDD) problem with a subexponential approximation factor on a class of integer lattices. The quantum algorithm uses a well-known but challenging-to-use quantum state on lattices as a type of approximate quantum eigenvector to randomly self-reduce the BDD instance to a random BDD instance which is solvable classically. The running time of the quantum algorithm is polynomial for one range of approximation factors and subexponential time for a second range of approximation factors. The subclass of lattices we study has a natural description in terms of the lattice's periodicity and finite abelian group rank. This view makes for a clean quantum algorithm in terms of finite abelian groups, uses very relatively little from lattice theory, and suggests exploring approximation algorithms for lattice problems in parameters other than dimension alone. A talk on this paper sparked many lively discussions and resulted in a new classical algorithm matching part of our result. We leave it as a challenge to give a classcial algorithm matching the general case.
翻译:我们用量子算法来解决某类整数拉特的分光近似系数(BDD)问题。 量子算法使用一种众所周知但具有挑战性的量子状态, 作为一种近似量量子源的种类, 将BDD实例随机地自降为随机的BDD实例, 这是一种典型的可溶性。 量子算法的运行时间是一系列近似系数的多元值和第二类近似系数的次伸缩时间。 我们研究的拉特克子类有关于拉蒂斯周期和有限亚贝利亚组等级的自然描述。 这个视图用有限的亚贝利亚组群来提出一种清洁量子算法, 相对很少使用 Lattice 理论, 并且建议探索光度以外的参数中拉蒂斯问题的近算法。 有关这个文件的演讲激发了许多活跃的讨论, 并产生了一种与我们结果相匹配的新古典算法部分。 我们保留它作为一个挑战, 来给一个类级算法来匹配一般案例。