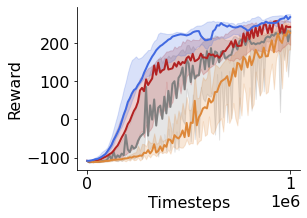
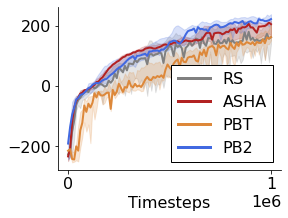
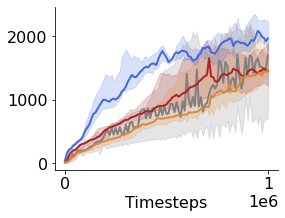
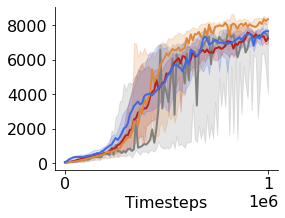
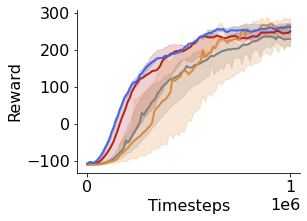
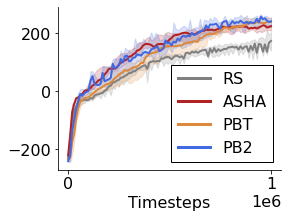
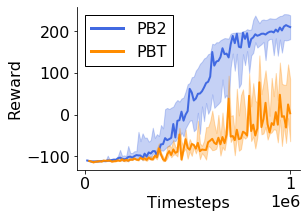
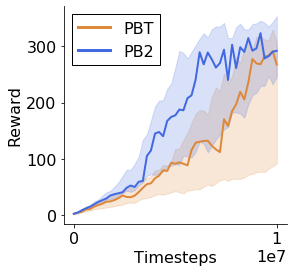
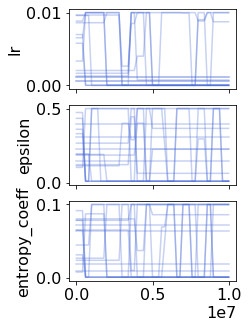
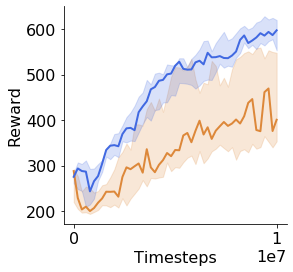
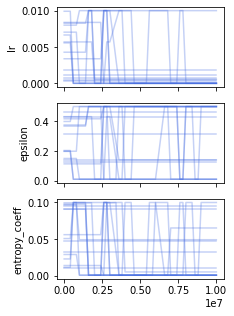
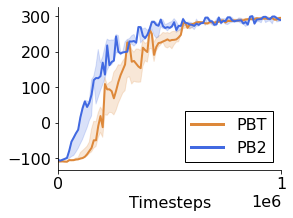
Many of the recent triumphs in machine learning are dependent on well-tuned hyperparameters. This is particularly prominent in reinforcement learning (RL) where a small change in the configuration can lead to failure. Despite the importance of tuning hyperparameters, it remains expensive and is often done in a naive and laborious way. A recent solution to this problem is Population Based Training (PBT) which updates both weights and hyperparameters in a single training run of a population of agents. PBT has been shown to be particularly effective in RL, leading to widespread use in the field. However, PBT lacks theoretical guarantees since it relies on random heuristics to explore the hyperparameter space. This inefficiency means it typically requires vast computational resources, which is prohibitive for many small and medium sized labs. In this work, we introduce the first provably efficient PBT-style algorithm, Population-Based Bandits (PB2). PB2 uses a probabilistic model to guide the search in an efficient way, making it possible to discover high performing hyperparameter configurations with far fewer agents than typically required by PBT. We show in a series of RL experiments that PB2 is able to achieve high performance with a modest computational budget.
翻译:近来在机器学习方面的许多成功都依赖于经过良好调整的超参数。 这在强化学习(RL)中特别突出,因为对配置进行小的改变可能导致失败。尽管调整超参数很重要,但费用仍然昂贵,而且往往以幼稚和艰苦的方式完成。这个问题的最近解决办法是人口培训(PBT),它更新了一个代理人员单一培训的重量和超参数。PBT已证明在RL中特别有效,导致外地的广泛使用。然而,PBT缺乏理论保障,因为它依靠随机的超参数空间探索。这种效率低通常意味着它需要大量的计算资源,而许多中小型实验室则无法使用这种资源。在这项工作中,我们采用了第一个效率很高的PBT型算法(PPB2)。 PB2使用一种概率模型来有效指导搜索,从而能够发现高性超参数配置,而比通常高的PB2级测试要低得多。我们用一个普通的PB2级测试来显示一个普通的PLT。