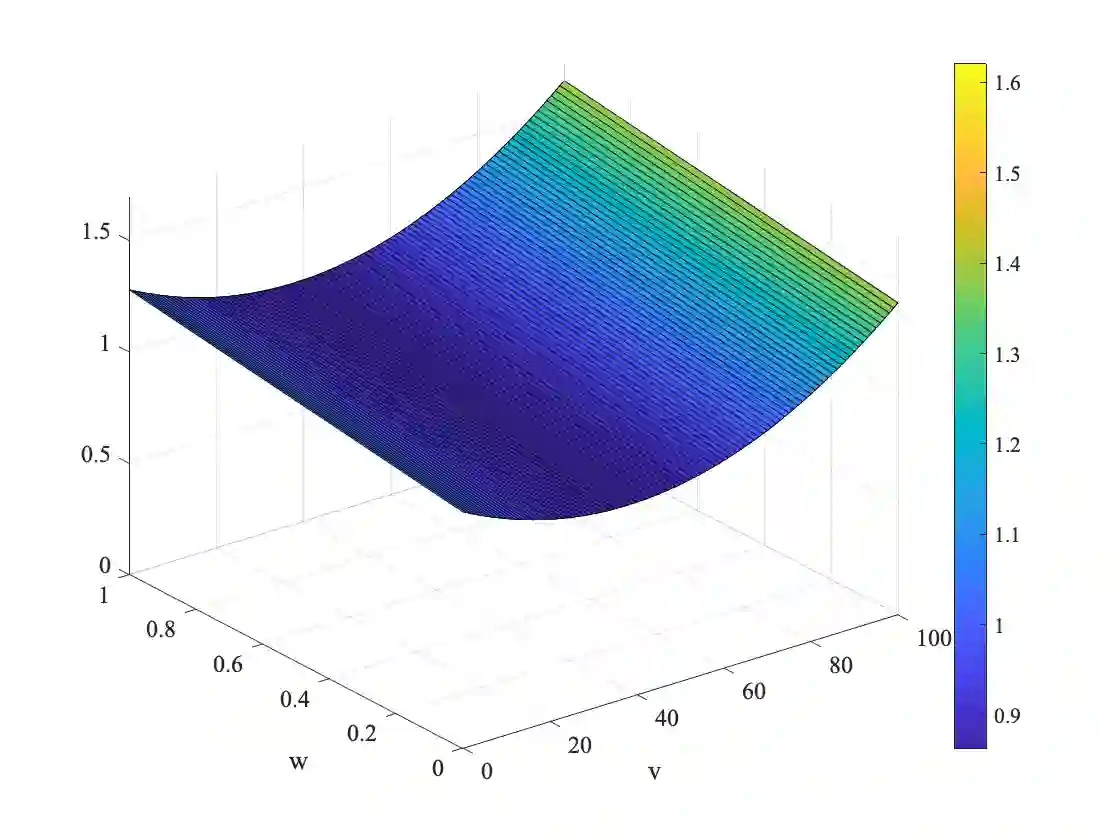
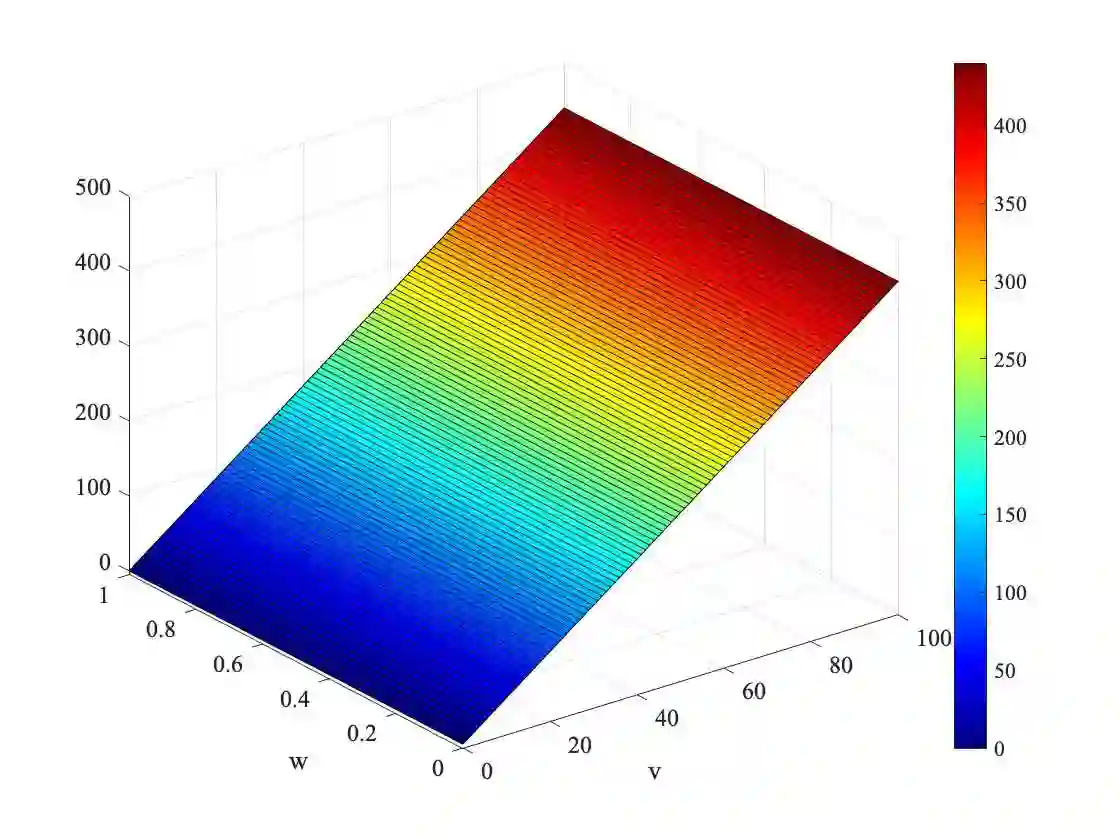
A novel theoretical convergence rate estimate for a Balancing Domain Decomposition by Constraints algorithm is proven for the solution of the cardiac Bidomain model, describing the propagation of the electric impulse in the cardiac tissue. The non-linear system arises from a fully implicit time discretization and a monolithic solution approach. The preconditioned non-symmetric operator is constructed from the linearized system arising within the Newton-Krylov approach for the solution of the non-linear problem; we theoretically analyze and prove a convergence rate bound for the Generalised Minimal Residual iterations' residual. The theory is confirmed by extensive parallel numerical tests, widening the class of robust and efficient solvers for implicit time discretizations of the Bidomain model.
翻译:非线性系统产生于完全隐含的时间分解和单一解析方法。 由牛顿-克利洛夫方法产生的线性非对称操作器是用来解决非线性问题的; 我们从理论上分析和证明普遍最小余值迭代剩余值的趋同率。 广泛平行的数字测试证实了这一理论,扩大了Bidomain模型内隐含时间分解的强大和高效解答器类别。