GD-VAEs: Geometric Dynamic Variational Autoencoders for Learning Nonlinear Dynamics and Dimension Reductions

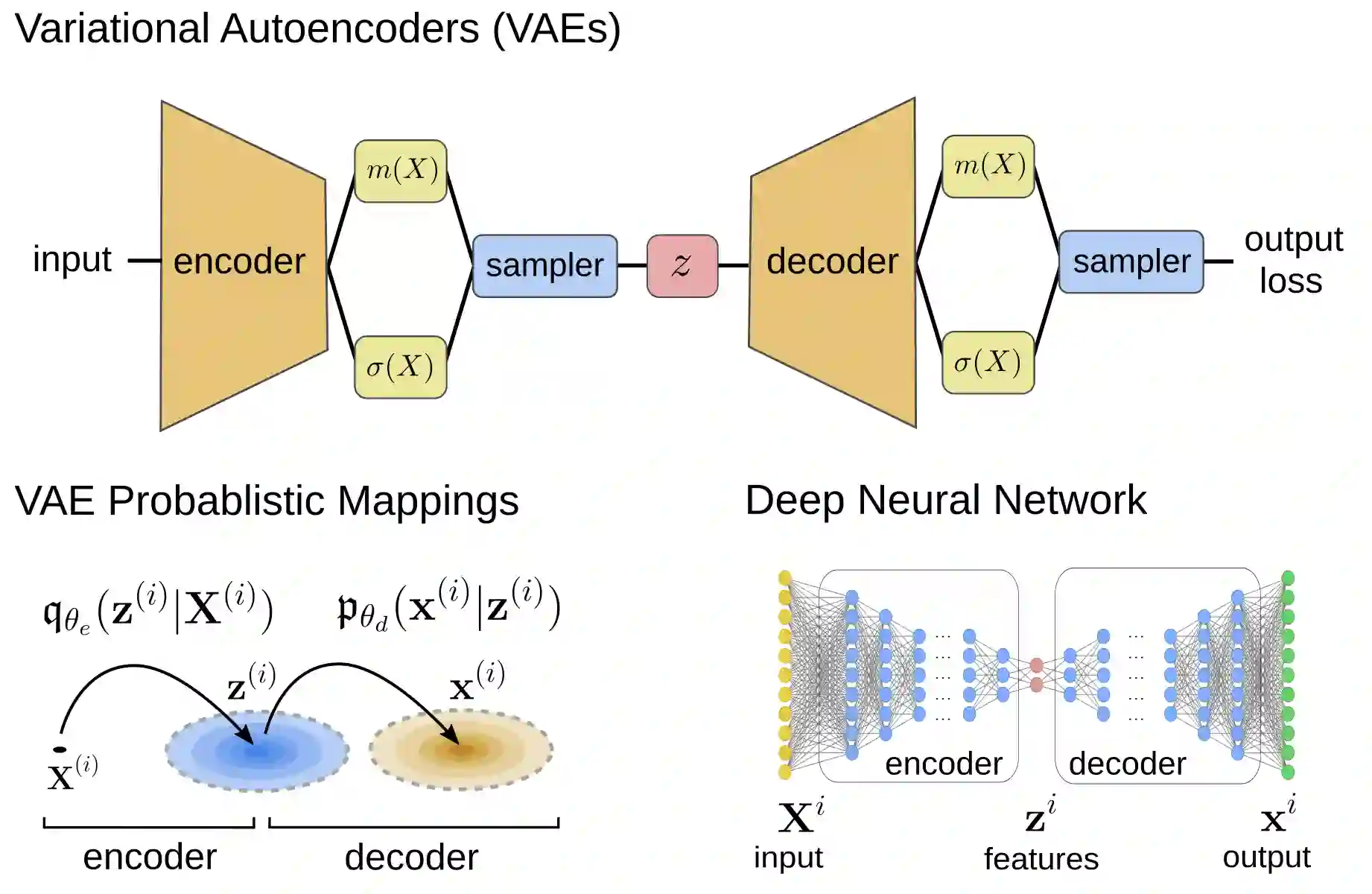
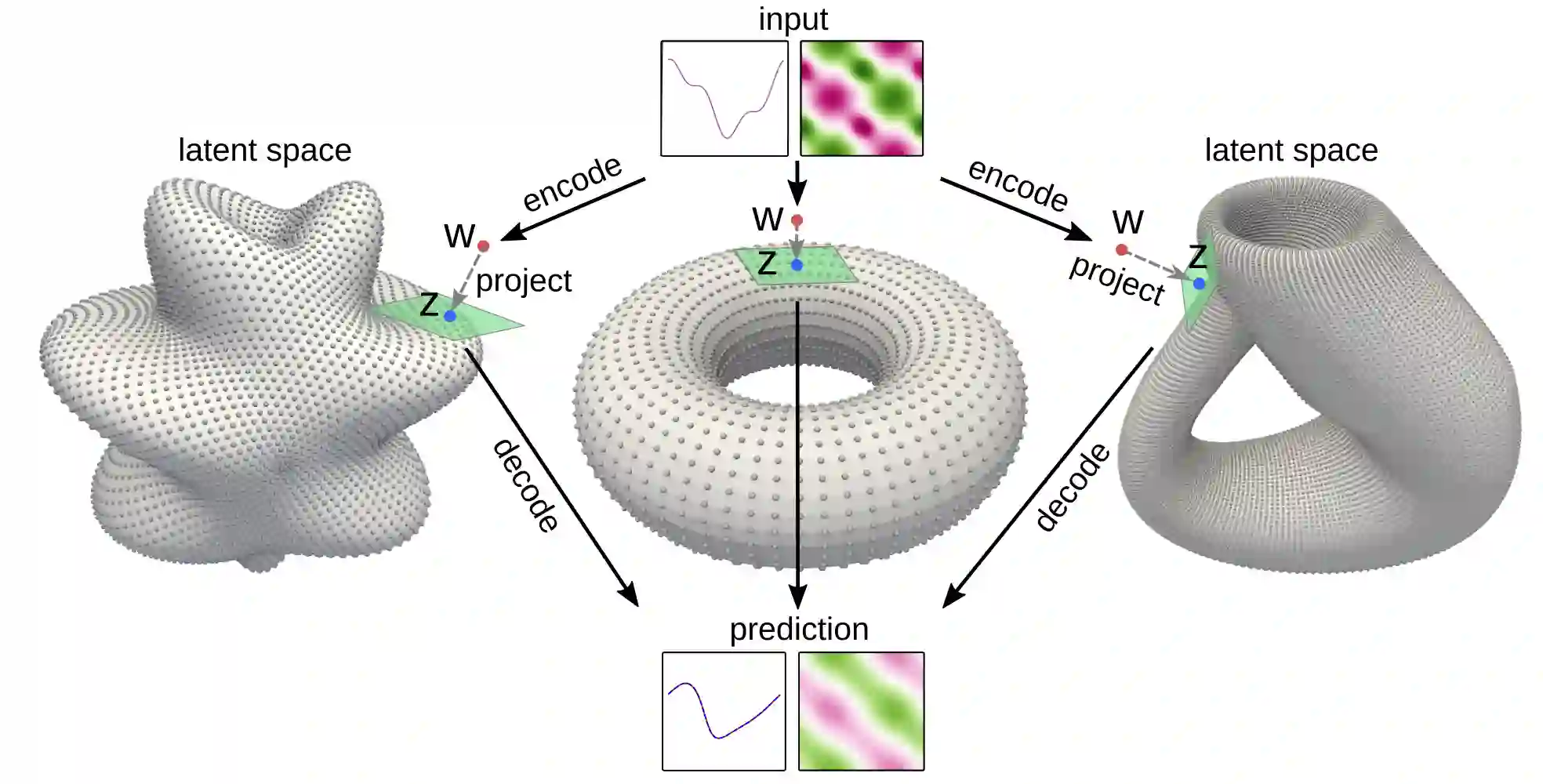
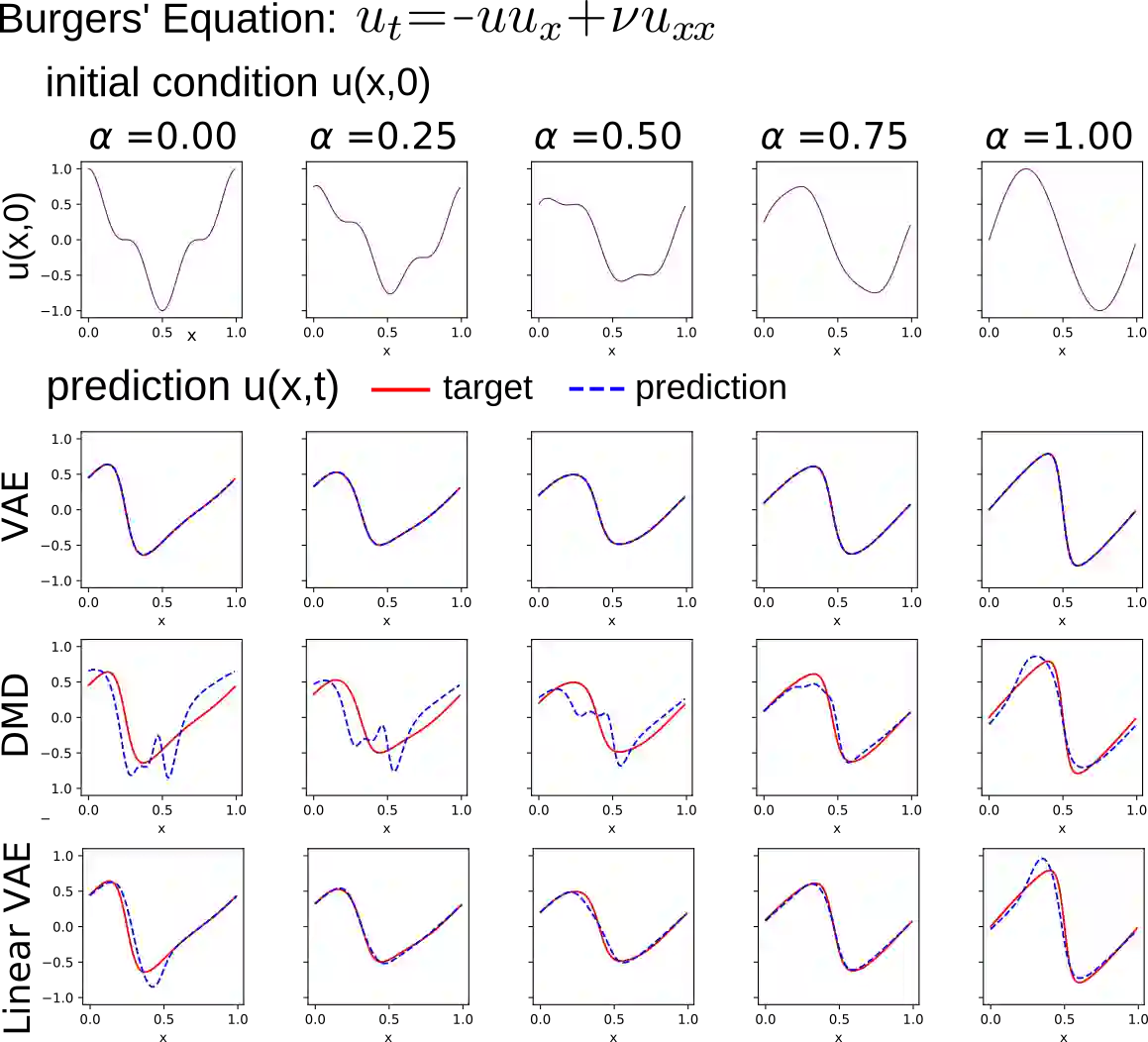
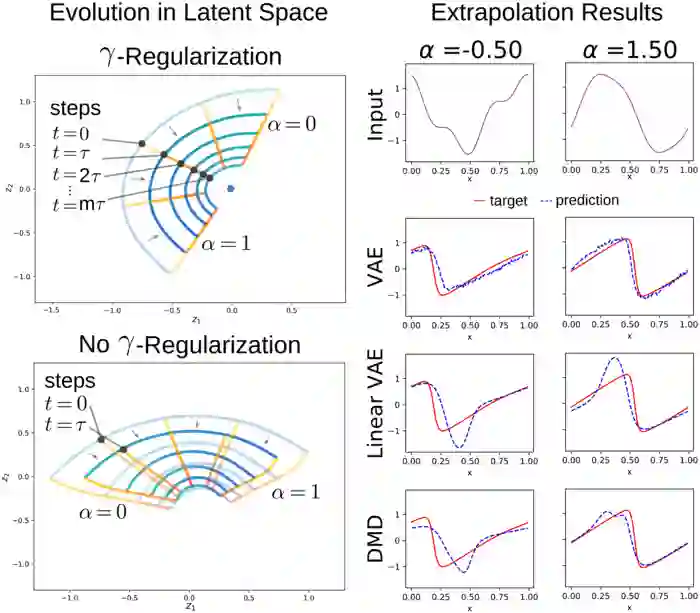
We develop data-driven methods incorporating geometric and topological information to learn parsimonious representations of nonlinear dynamics from observations. We develop approaches for learning nonlinear state space models of the dynamics for general manifold latent spaces using training strategies related to Variational Autoencoders (VAEs). Our methods are referred to as Geometric Dynamic (GD) Variational Autoencoders (GD-VAEs). We learn encoders and decoders for the system states and evolution based on deep neural network architectures that include general Multilayer Perceptrons (MLPs), Convolutional Neural Networks (CNNs), and Transpose CNNs (T-CNNs). Motivated by problems arising in parameterized PDEs and physics, we investigate the performance of our methods on tasks for learning low dimensional representations of the nonlinear Burgers equations, constrained mechanical systems, and spatial fields of reaction-diffusion systems. GD-VAEs provide methods for obtaining representations for use in learning tasks involving dynamics.