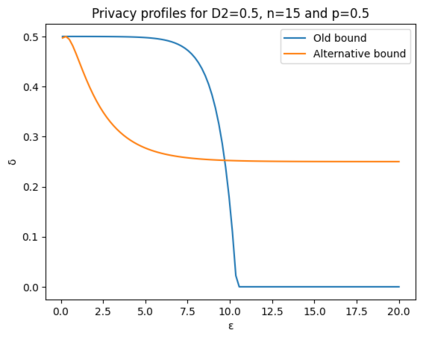
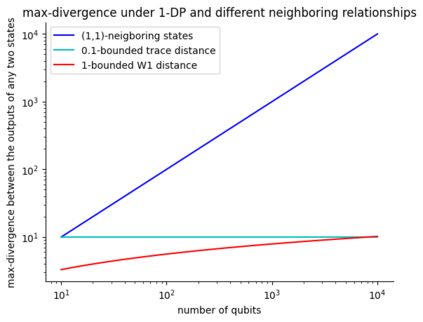
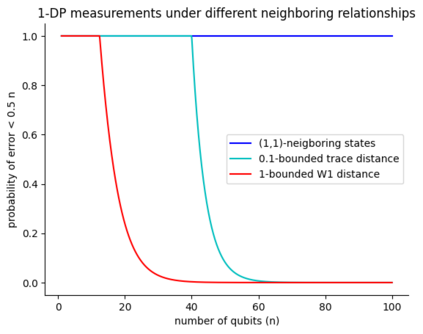
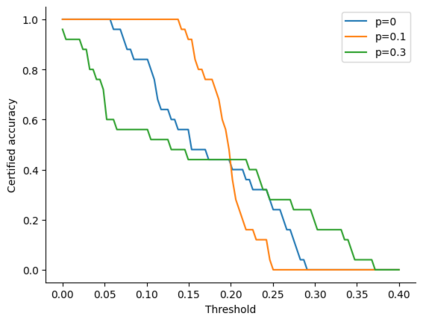
Differential privacy is a widely used notion of security that enables the processing of sensitive information. In short, differentially private algorithms map "neighbouring" inputs to close output distributions. Prior work proposed several quantum extensions of differential privacy, each of them built on substantially different notions of neighbouring quantum states. In this paper, we propose a novel and general definition of neighbouring quantum states. We demonstrate that this definition captures the underlying structure of quantum encodings and can be used to provide exponentially tighter privacy guarantees for quantum measurements. Our approach combines the addition of classical and quantum noise and is motivated by the noisy nature of near-term quantum devices. Moreover, we also investigate an alternative setting where we are provided with multiple copies of the input state. In this case, differential privacy can be ensured with little loss in accuracy combining concentration of measure and noise-adding mechanisms. En route, we prove the advanced joint convexity of the quantum hockey-stick divergence and we demonstrate how this result can be applied to quantum differential privacy. Finally, we complement our theoretical findings with an empirical estimation of the certified adversarial robustness ensured by differentially private measurements.
翻译:暂无翻译
相关内容
- Today (iOS and OS X): widgets for the Today view of Notification Center
- Share (iOS and OS X): post content to web services or share content with others
- Actions (iOS and OS X): app extensions to view or manipulate inside another app
- Photo Editing (iOS): edit a photo or video in Apple's Photos app with extensions from a third-party apps
- Finder Sync (OS X): remote file storage in the Finder with support for Finder content annotation
- Storage Provider (iOS): an interface between files inside an app and other apps on a user's device
- Custom Keyboard (iOS): system-wide alternative keyboards
Source: iOS 8 Extensions: Apple’s Plan for a Powerful App Ecosystem