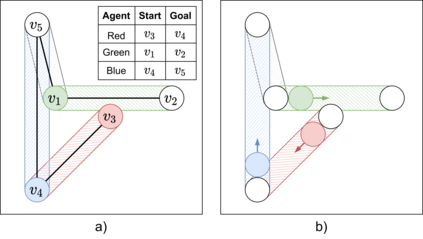
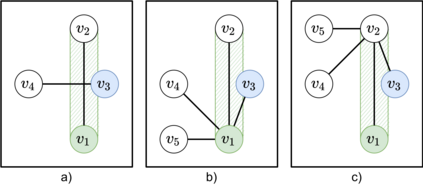
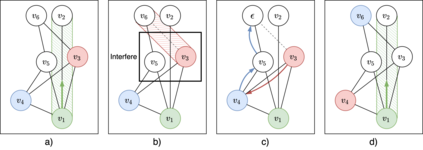
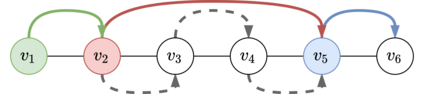
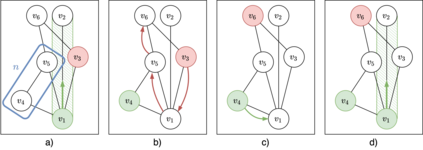
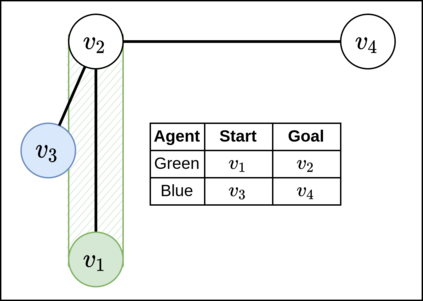
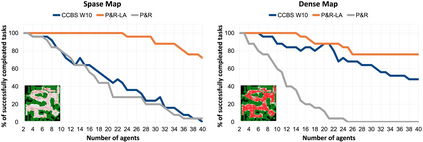
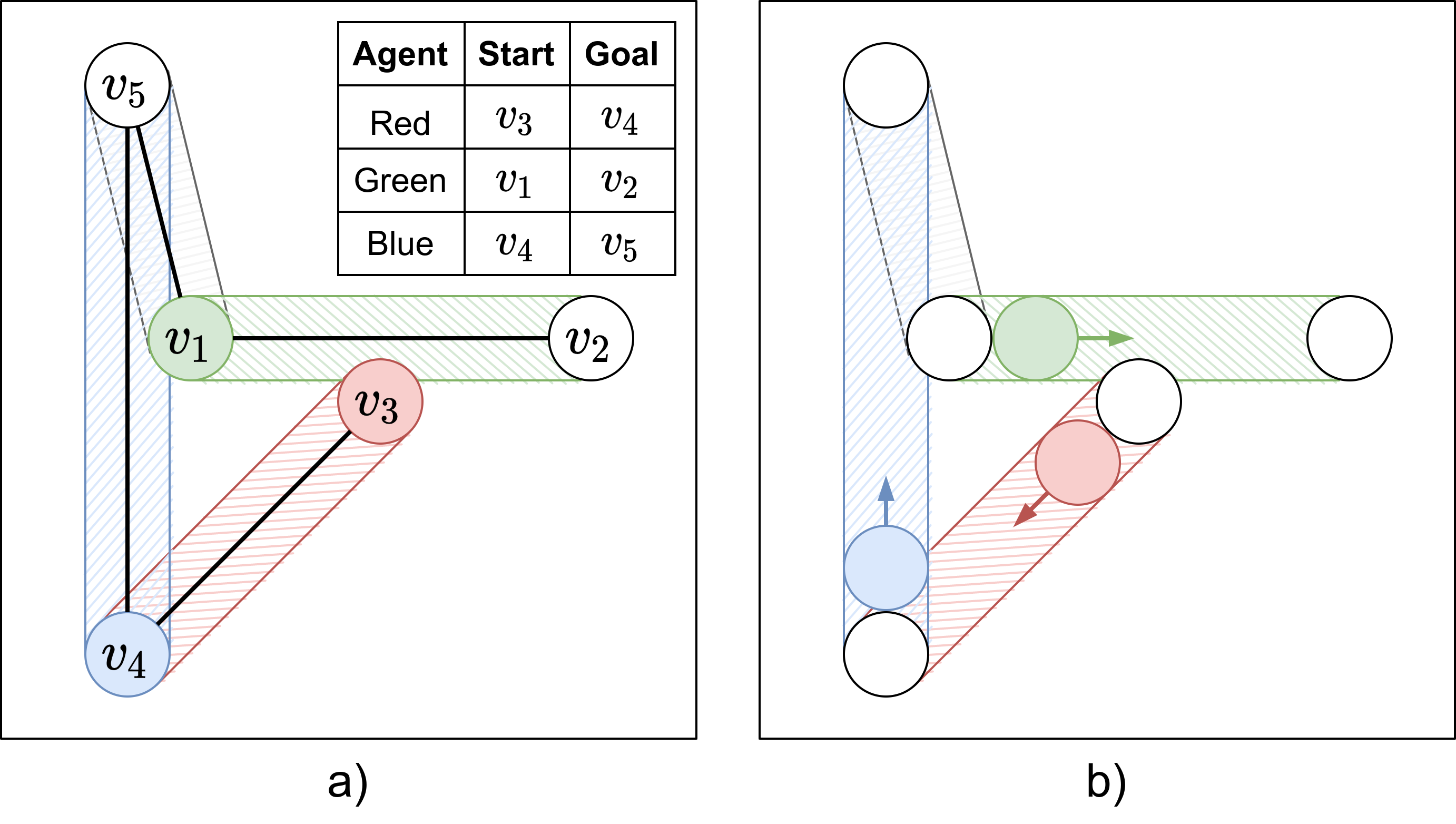
Multi-agent pathfinding (MAPF) is a challenging problem which is hard to solve optimally even when simplifying assumptions are adopted, e.g. planar graphs (typically -- grids), discretized time, uniform duration of move and wait actions etc. On the other hand, MAPF under such restrictive assumptions (also known as the Classical MAPF) is equivalent to the so-called pebble motion problem for which non-optimal polynomial time algorithms do exist. Recently, a body of works emerged that investigated MAPF beyond the basic setting and, in particular, considered agents of arbitrary size and shape. Still, to the best of our knowledge no complete algorithms for such MAPF variant exists. In this work we attempt to narrow this gap by considering MAPF for large agents and suggesting how this problem can be reduced to pebble motion on (general) graphs. The crux of this reduction is the procedure that moves away the agents away from the edge which is needed to perform a move action of the current agent. We consider different variants of how this procedure can be implemented and present a variant of the pebble motion algorithm which incorporates this procedure. Unfortunately, the algorithm is still incomplete, but empirically we show that it is able to solve much more MAPF instances (under the strict time limit) with large agents on arbitrary non-planar graphs (roadmaps) compared to the state-of-the-art MAPF solver -- Continous Conflict-Based Search (CCBS).
翻译:多试剂路由调查(MAPF)是一个具有挑战性的问题,即使采用简化的假设,例如平面图(通常 -- -- 网格)、离散的时间、移动和等待行动的统一时间等等,也很难以最佳的方式解决。 另一方面,在这种限制性假设(又称经典MAPF)下,MAPF相当于所谓的卵泡运动问题,因为非最佳多时算法确实存在。最近,出现了一套调查MAPF的工程,在基本环境之外,特别是考虑到任意大小和形状的代理人。但据我们所知,这种MAPF变异的全算法还不存在。在这项工作中,我们试图缩小这一差距,办法是考虑MAPF对大型代理人的MAPF,并建议如何将这一问题减为(一般)图上的微粒运动。这种减法的核心是使代理人脱离目前代理人的移动动作所需的边缘的程序。我们考虑了如何执行这一程序的不同变式,并且提出了这种程序是如何执行的任意尺寸和形状的代理人的变式。我们试图缩小这种变式的MAPFMFA(我们不完全地算)在不完全的轨道上,比MAPFLA(可以比较地算)。