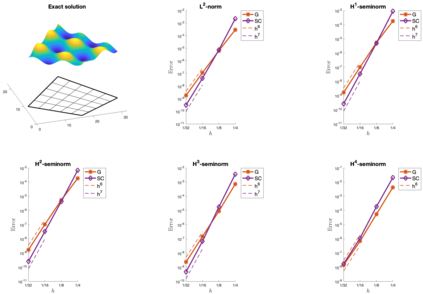
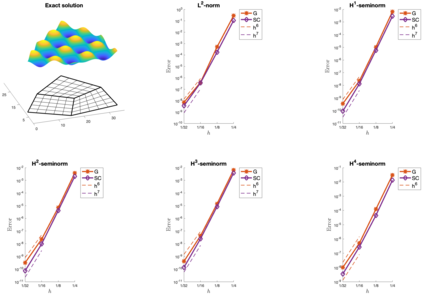
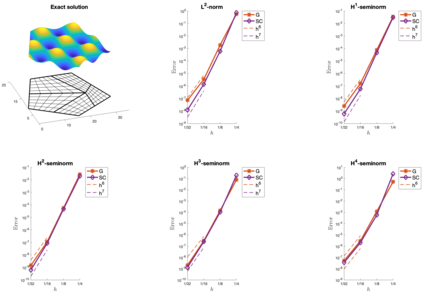
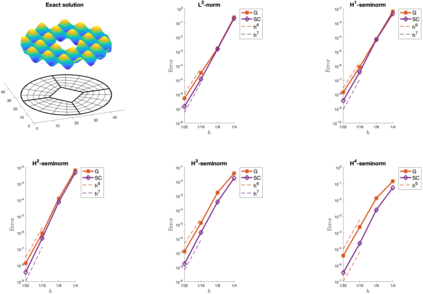
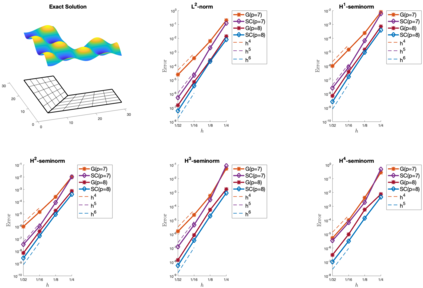
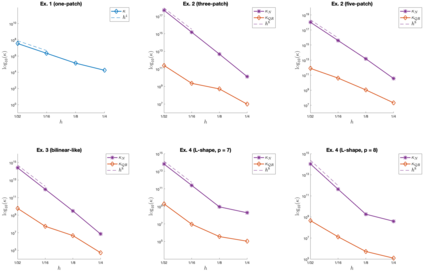
We present an isogeometric collocation method for solving the biharmonic equation over planar bilinearly parameterized multi-patch domains. The developed approach is based on the use of the globally $C^4$-smooth isogeometric spline space [34] to approximate the solution of the considered partial differential equation, and proposes as collocation points two different choices, namely on the one hand the Greville points and on the other hand the so-called superconvergent points. Several examples demonstrate the potential of our collocation method for solving the biharmonic equation over planar multi-patch domains, and numerically study the convergence behavior of the two types of collocation points with respect to the $L^2$-norm as well as to equivalents of the $H^s$-seminorms for $1 \leq s \leq 4$. In the studied case of spline degree $p=9$, the numerical results indicate in case of the Greville points a convergence of order $\mathcal{O}(h^{p-3})$ independent of the considered (semi)norm, and show in case of the superconvergent points an improved convergence of order $\mathcal{O}(h^{p-2})$ for all (semi)norms except for the equivalent of the $H^4$-seminorm, where the order $\mathcal{O}(h^{p-3})$ is anyway optimal.
翻译:暂无翻译