Singularly Near Optimal Leader Election in Asynchronous Networks

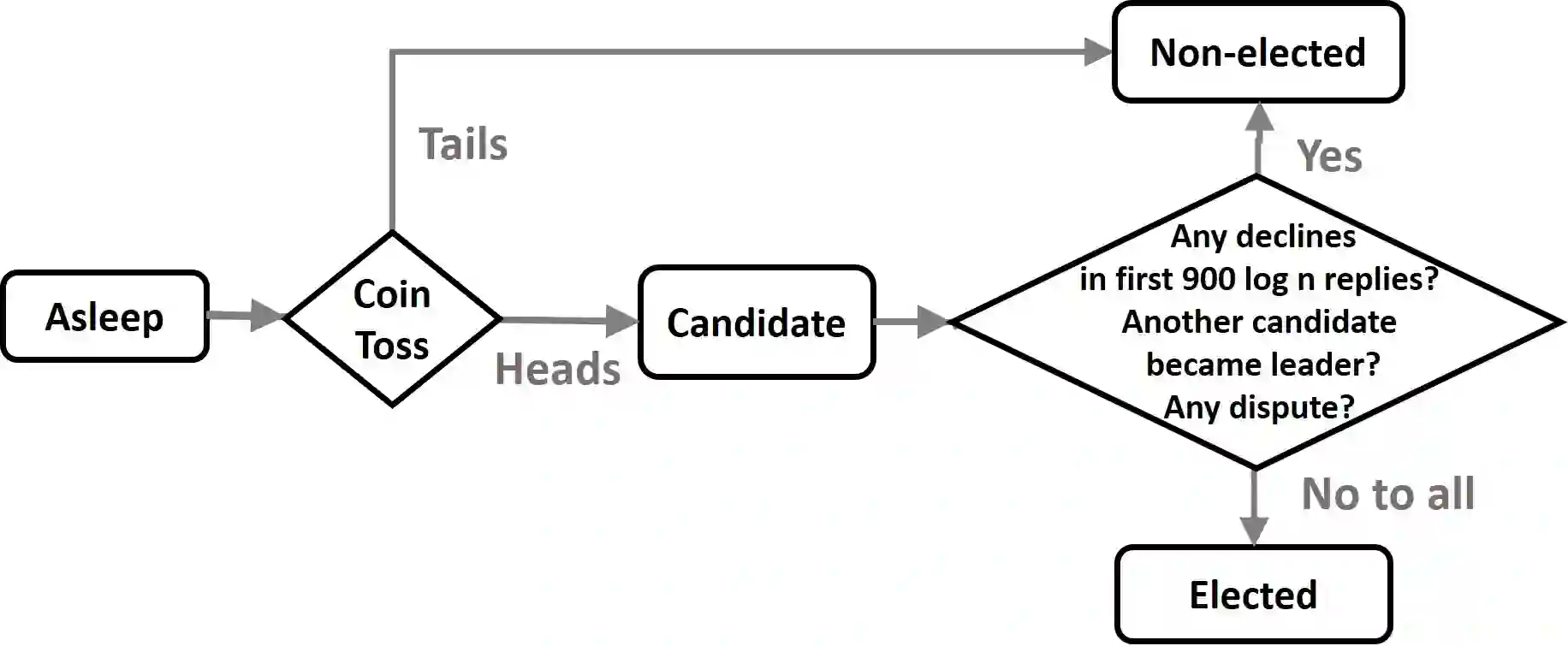
This paper concerns designing distributed algorithms that are {\em singularly optimal}, i.e., algorithms that are {\em simultaneously} time and message {\em optimal}, for the fundamental leader election problem in {\em asynchronous} networks. Kutten et al. (JACM 2015) presented a singularly near optimal randomized leader election algorithm for general {\em synchronous} networks that ran in $O(D)$ time and used $O(m \log n)$ messages (where $D$, $m$, and $n$ are the network's diameter, number of edges and number of nodes, respectively) with high probability.\footnote{Throughout, "with high probability" means "with probability at least $1-1/n^c$, for constant $c$."} Both bounds are near optimal (up to a logarithmic factor), since $\Omega(D)$ and $\Omega(m)$ are the respective lower bounds for time and messages for leader election even for synchronous networks and even for (Monte-Carlo) randomized algorithms. On the other hand, for general asynchronous networks, leader election algorithms are only known that are either time or message optimal, but not both. Kutten et al. (DISC 2020) presented a randomized asynchronous leader election algorithm that is singularly near optimal for \emph{complete networks}, but left open the problem for general networks. This paper shows that singularly near optimal (up to polylogarithmic factors) bounds can be achieved for general {\em asynchronous} networks. We present a randomized singularly near optimal leader election algorithm that runs in $O(D + \log^2n)$ time and $O(m\log^2 n)$ messages with high probability. Our result is the first known distributed leader election algorithm for asynchronous networks that is near optimal with respect to both time and message complexity and improves over a long line of results including the classical results of Gallager et al. (ACM TOPLAS, 1983), Peleg (JPDC, 1989), and Awerbuch (STOC 89).