Topological Data Analysis through alignment of Persistence Landscapes

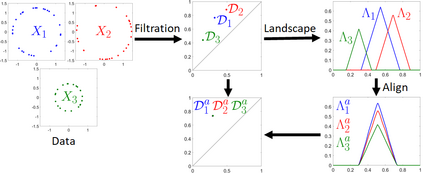
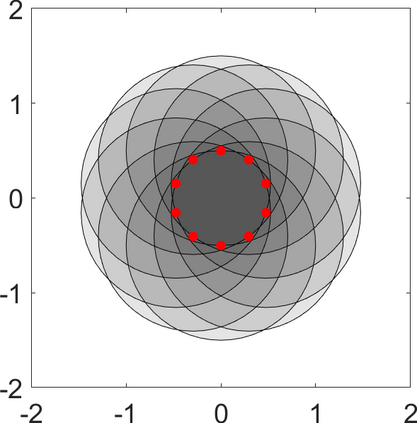
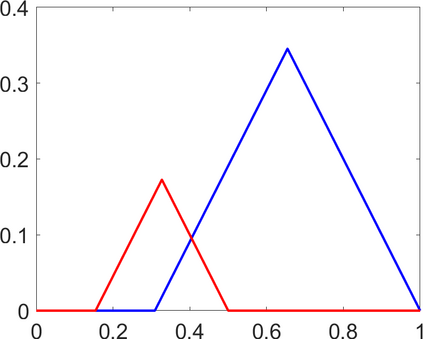
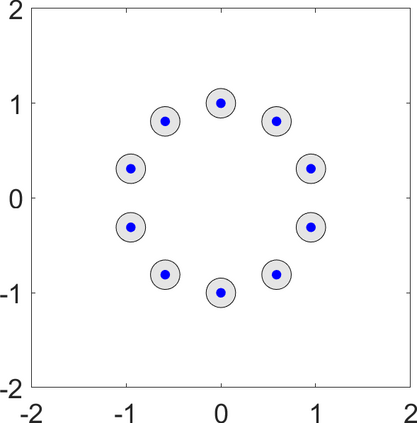
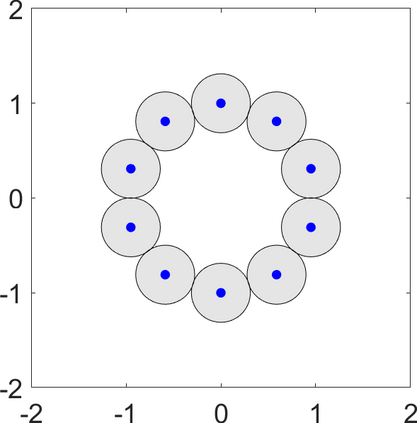
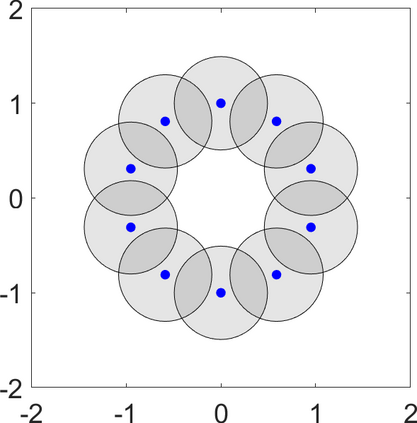
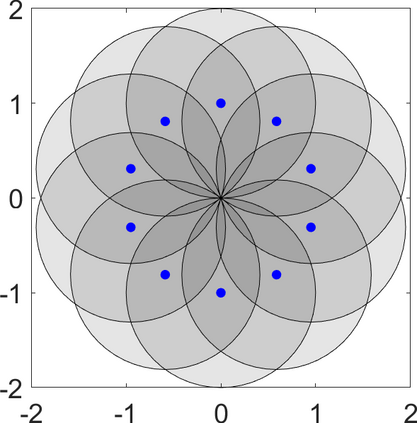
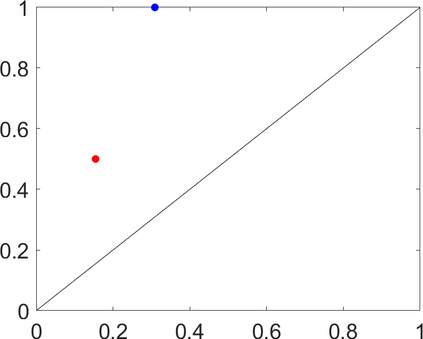
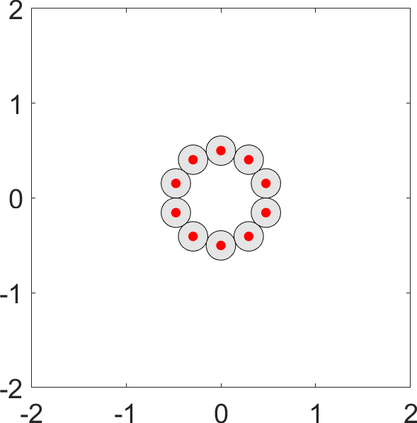
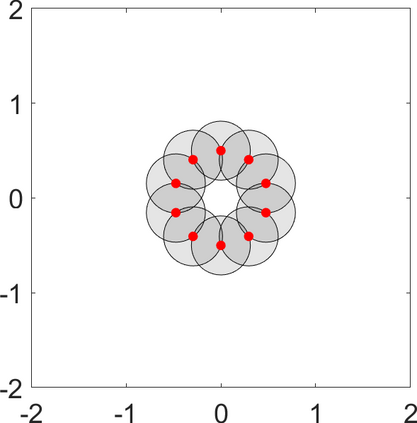
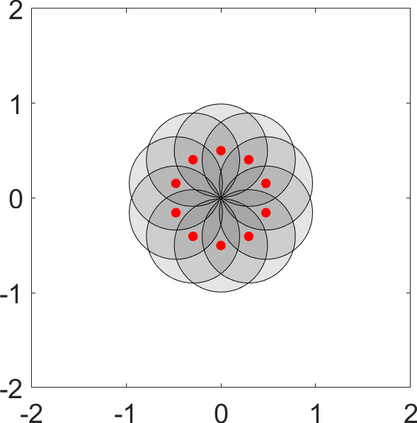
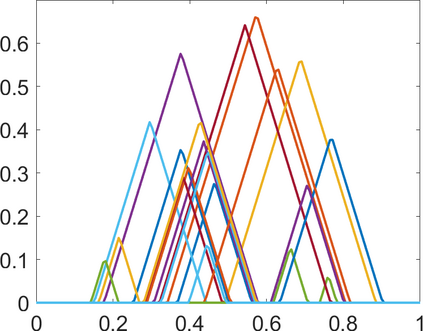
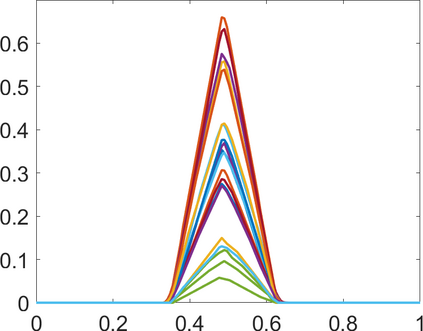
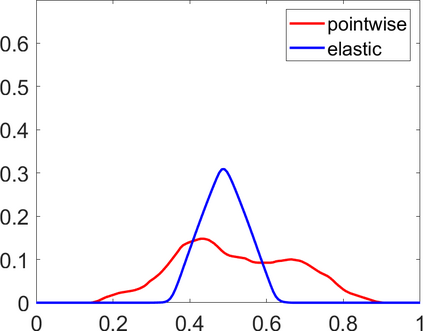
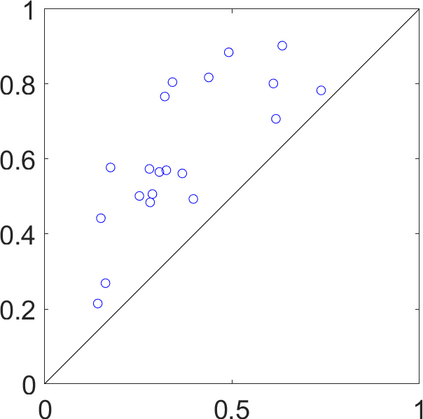
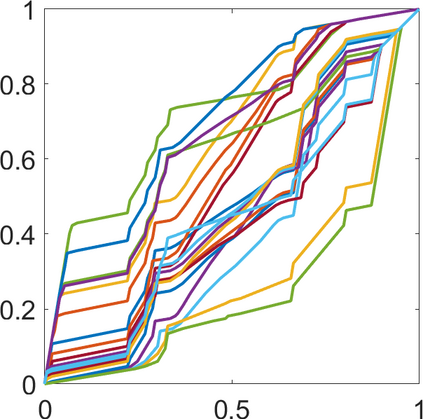
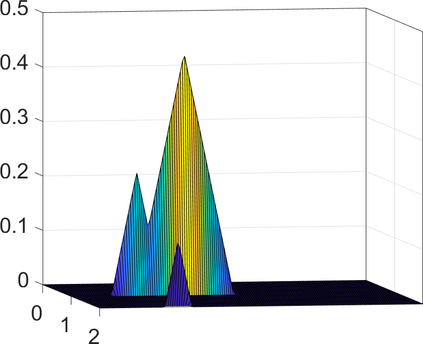
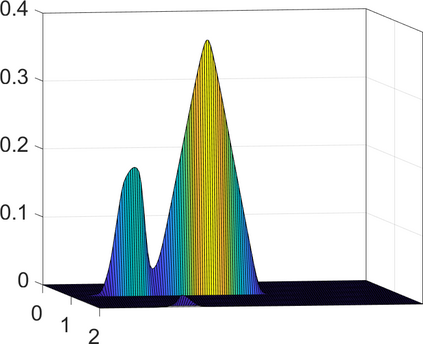
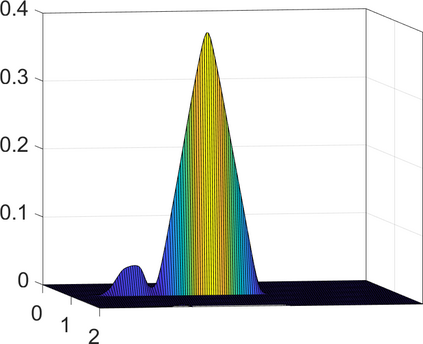
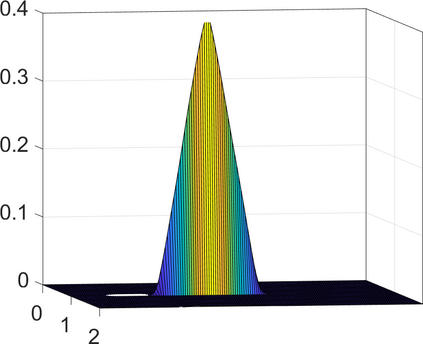
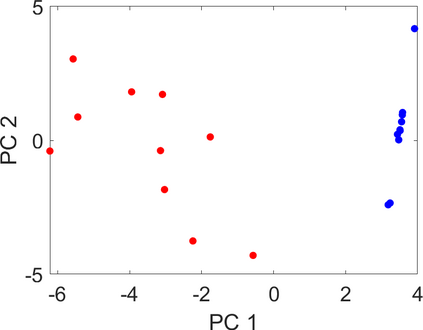
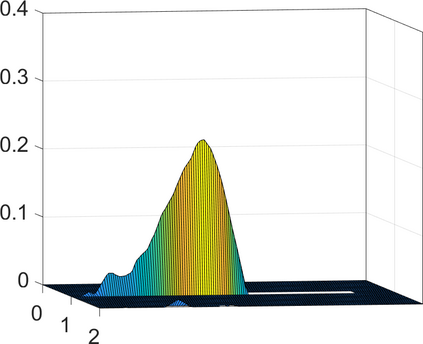
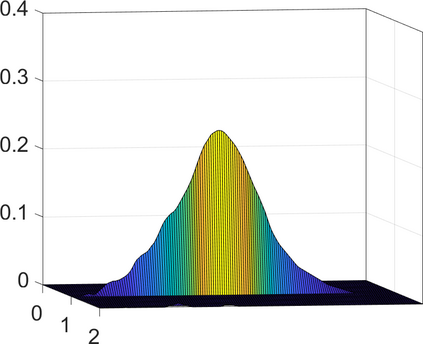
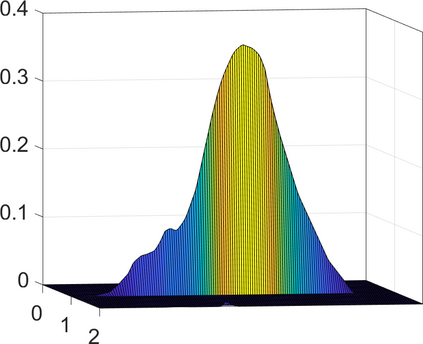
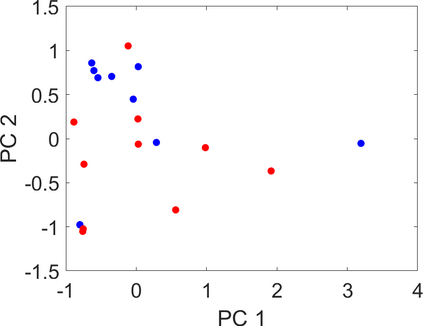
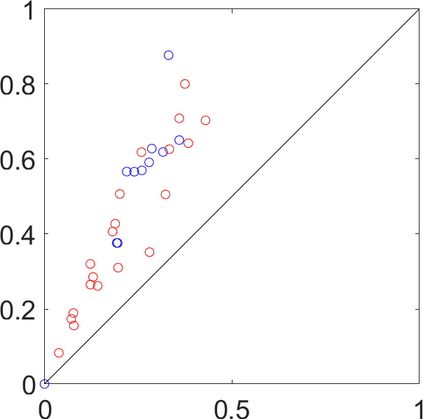
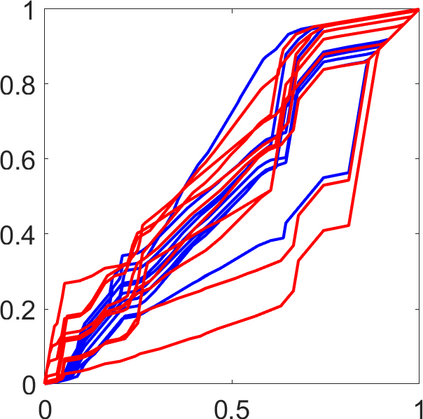
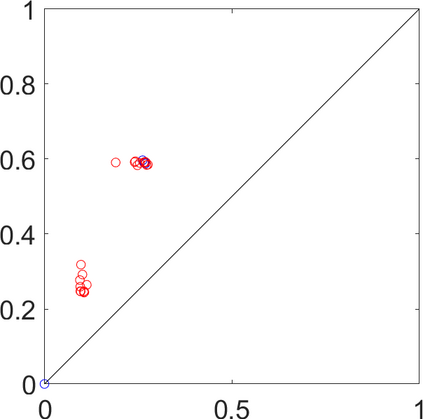
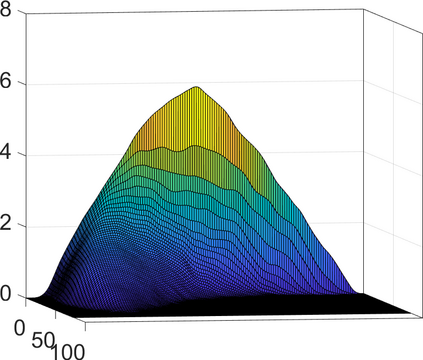
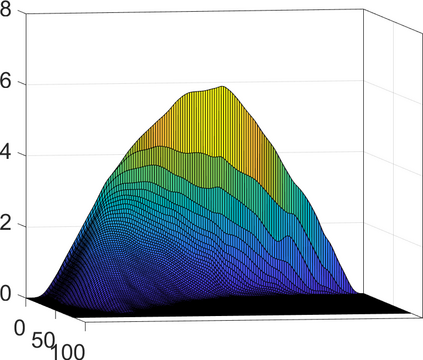
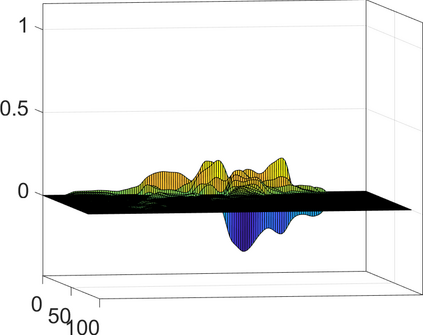
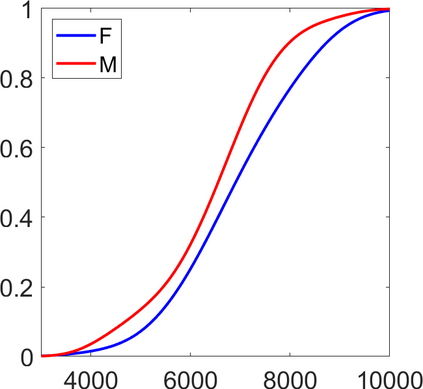
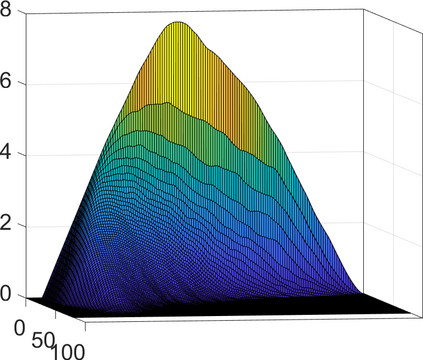
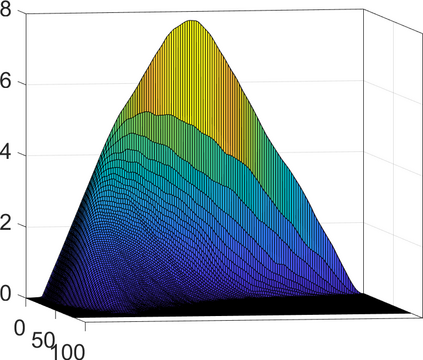
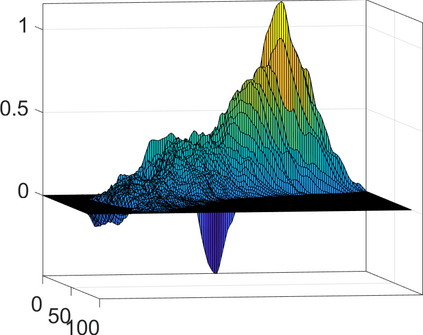
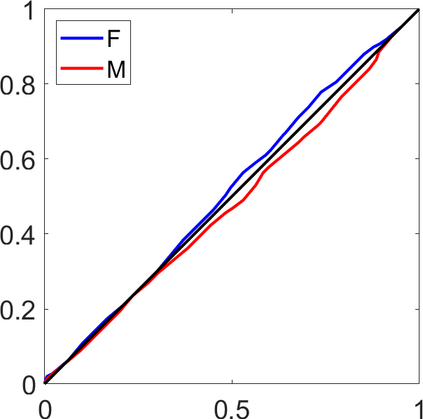
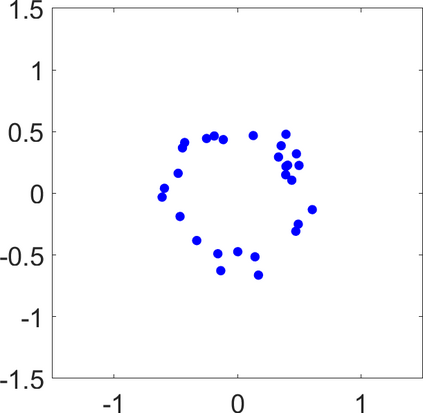
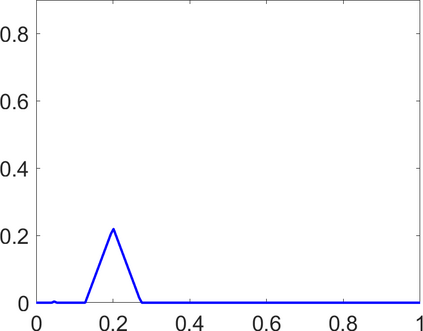
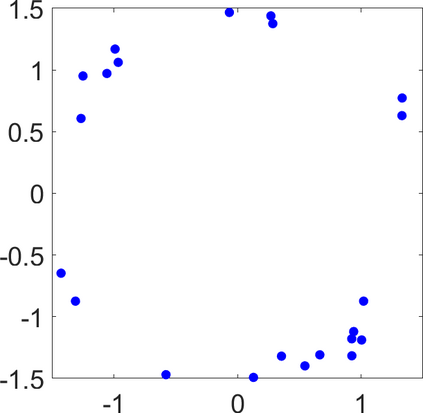
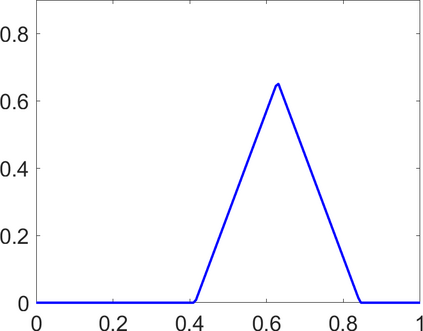
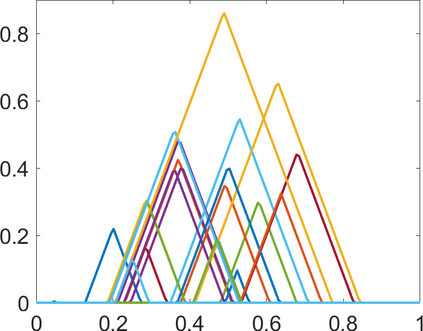
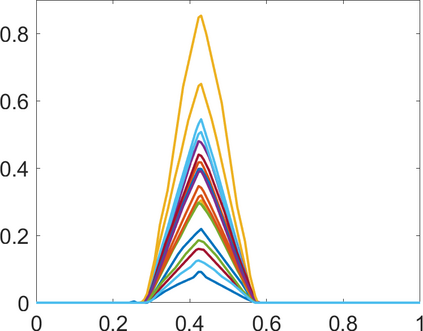
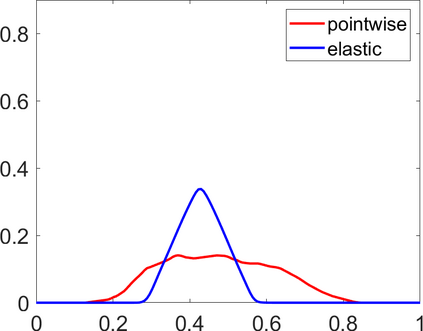
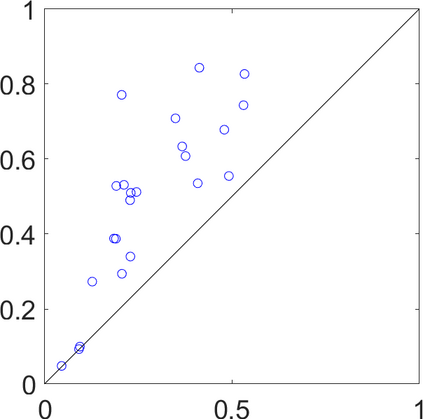
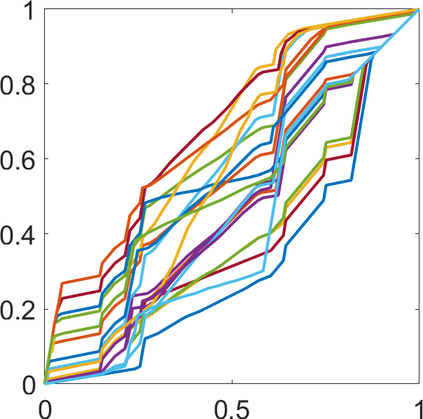
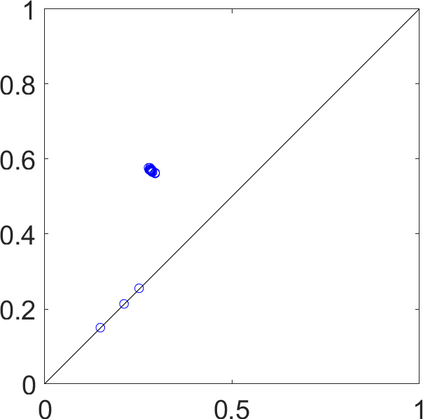
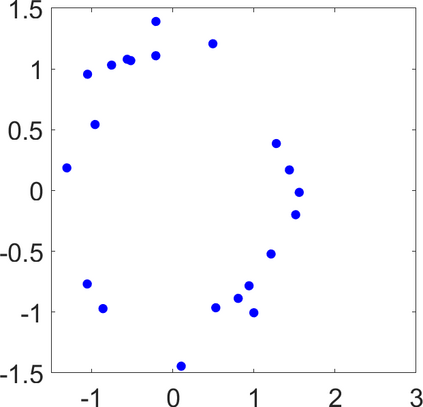
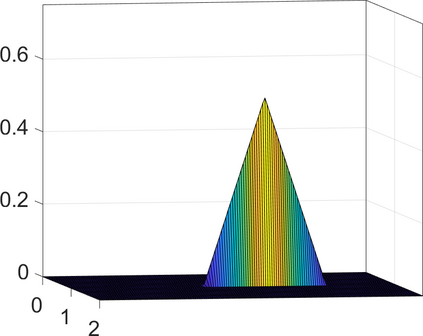
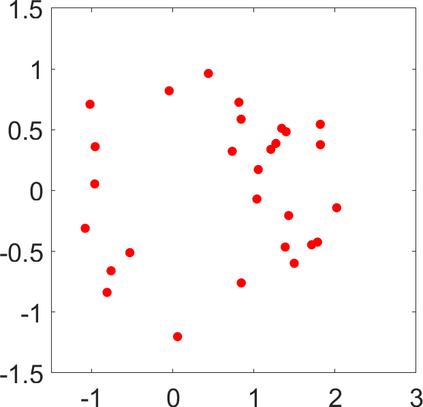
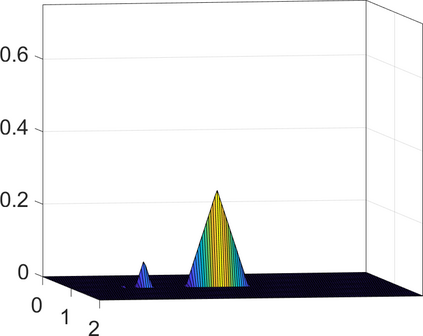
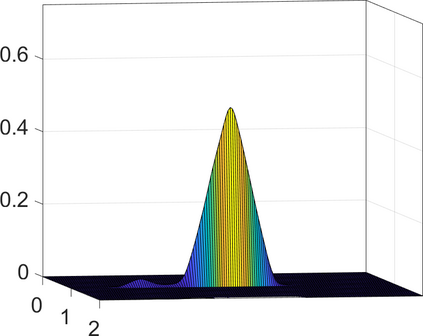
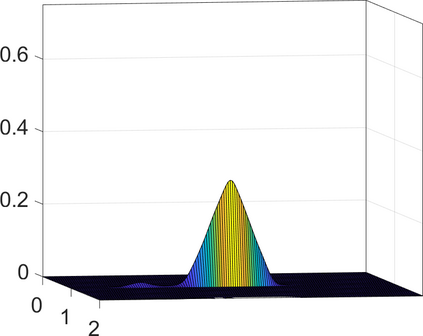
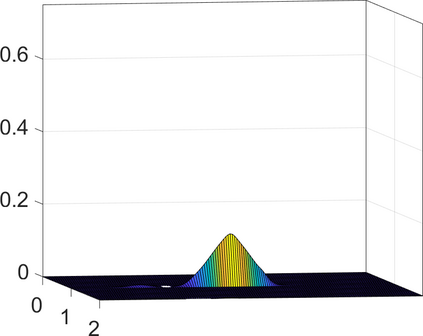
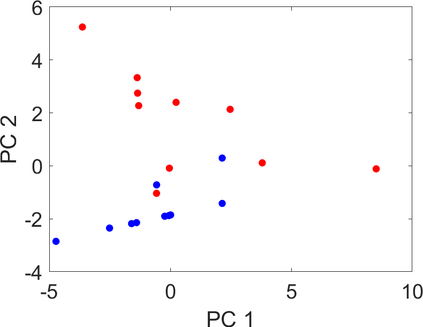
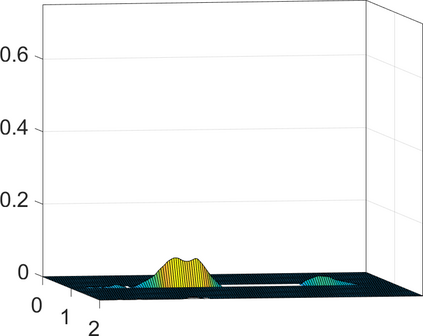
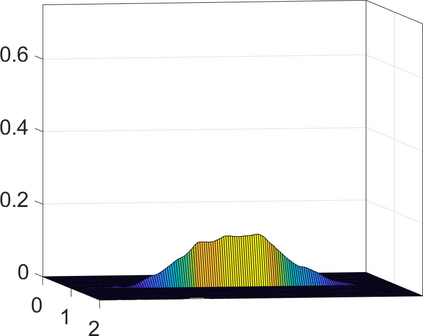
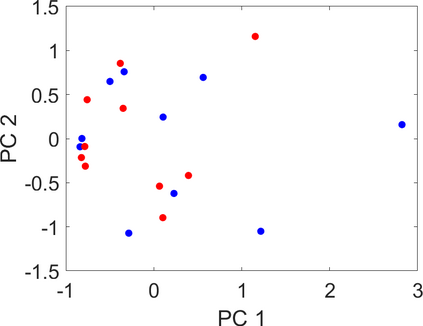
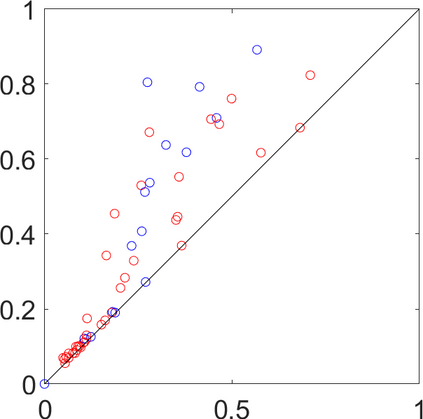
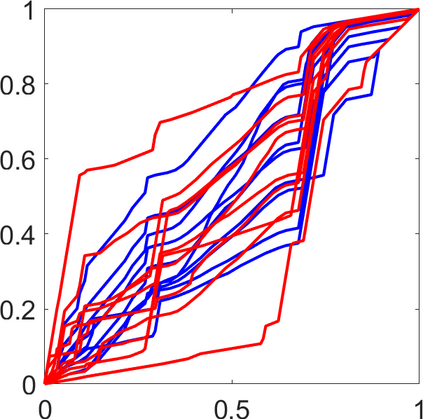
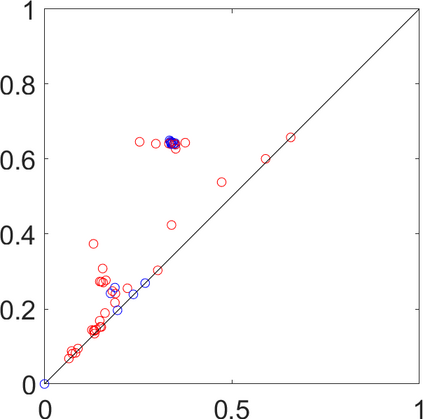
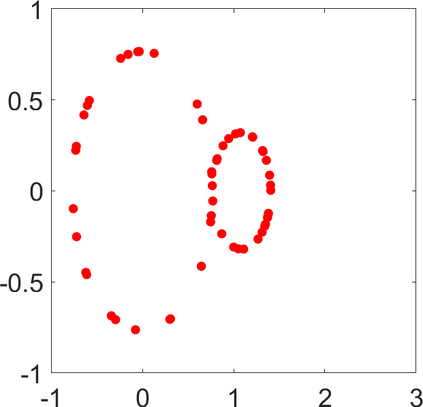
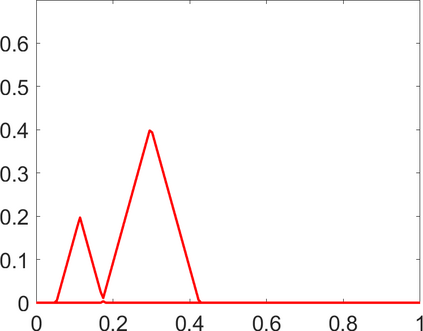
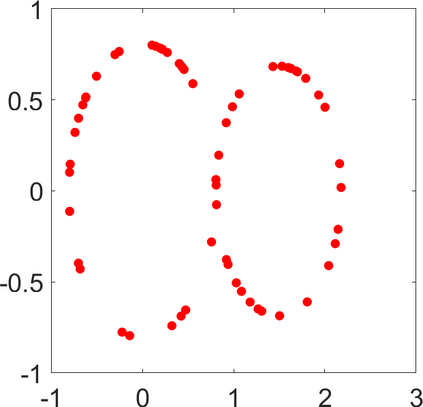
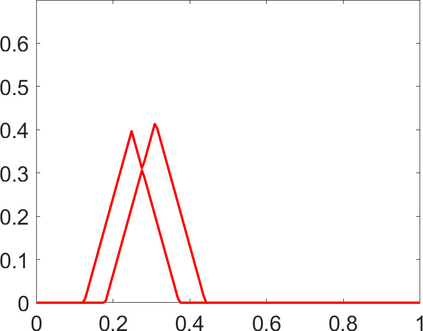
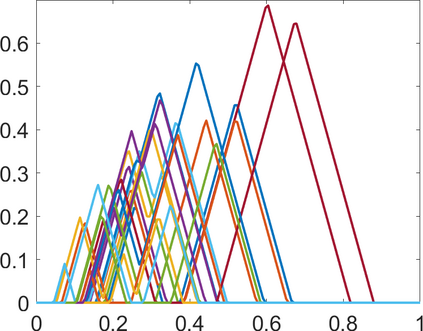
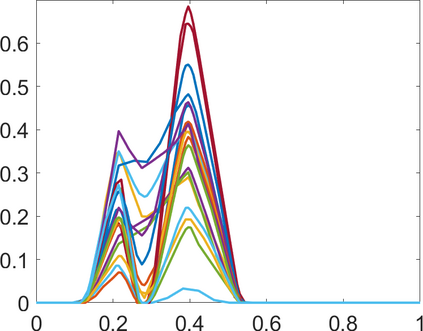
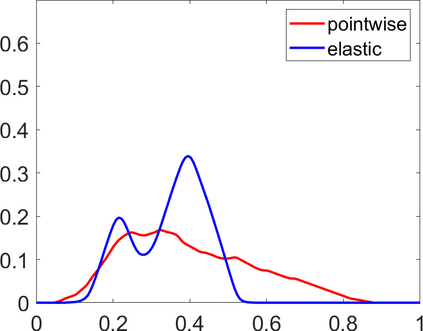
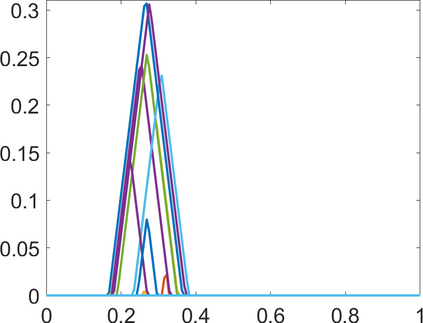
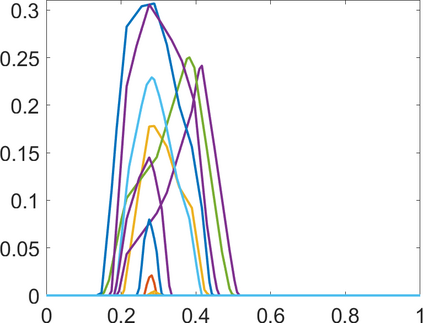
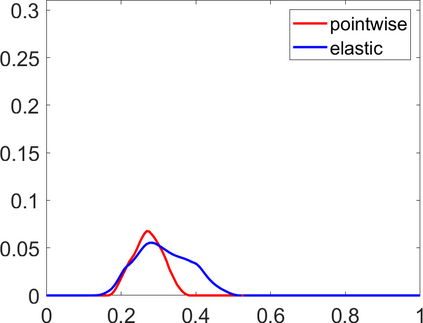
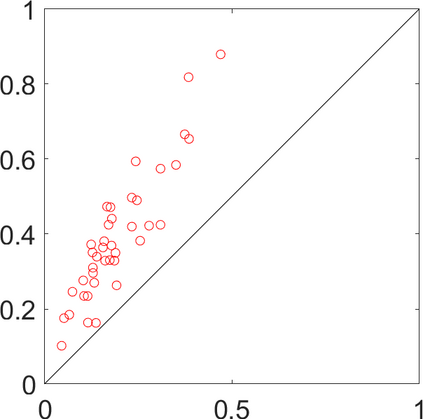
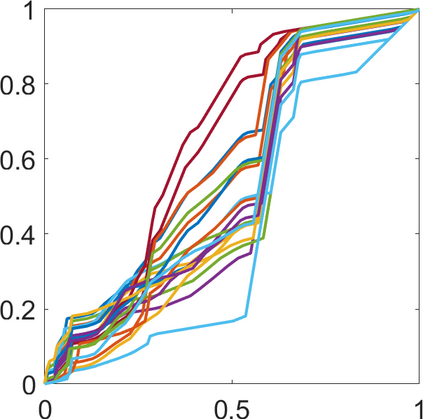
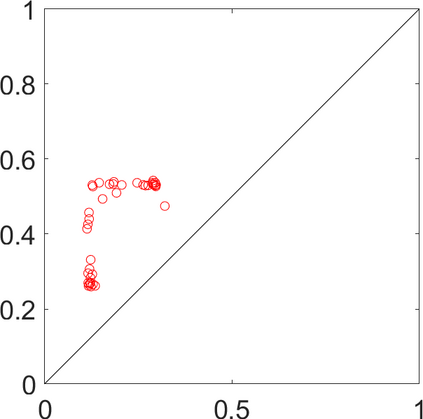
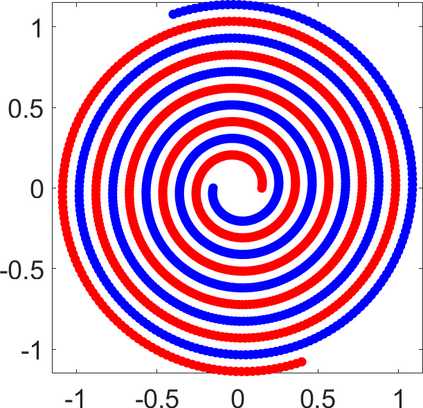
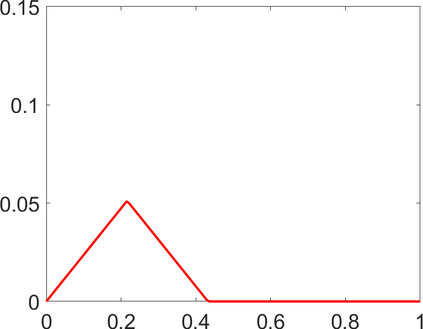
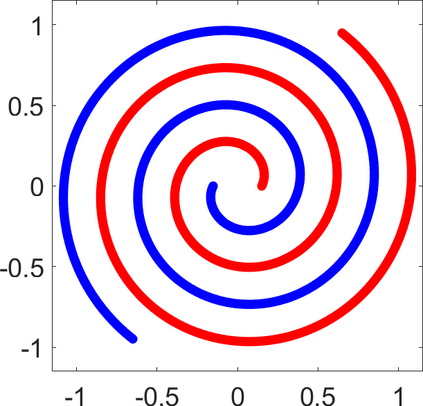
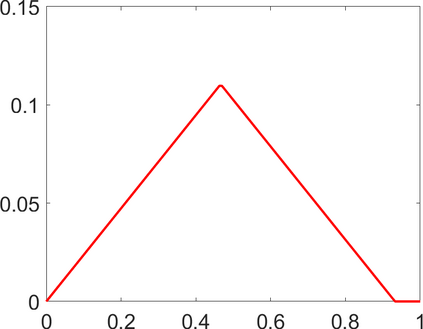
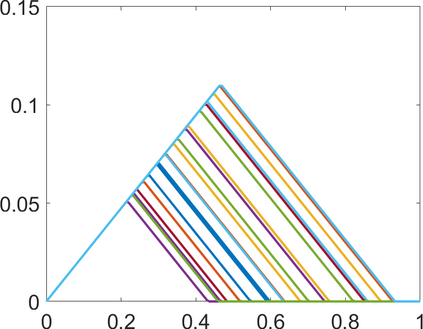
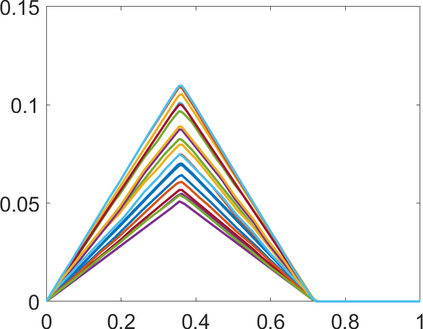
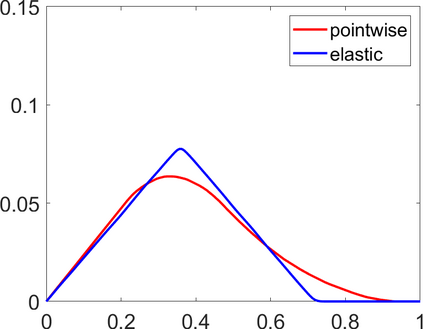
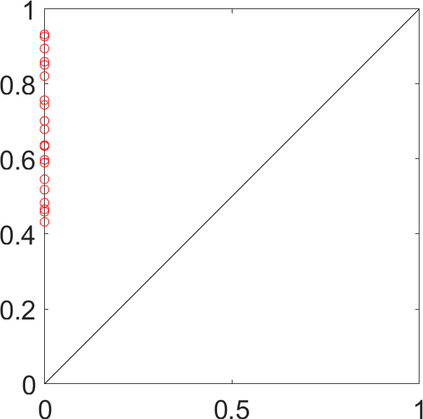
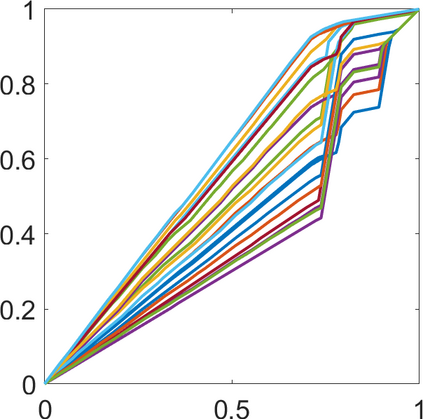
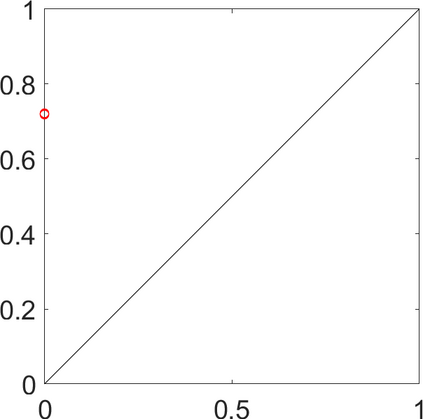
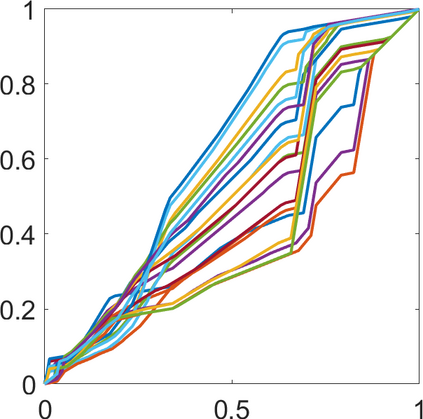
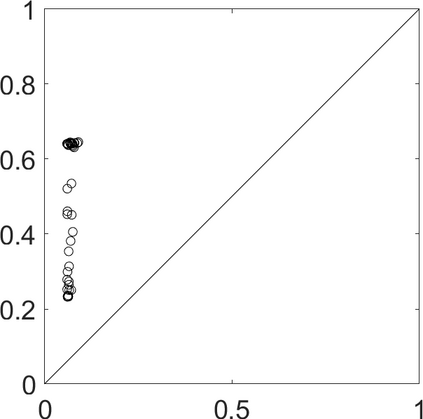
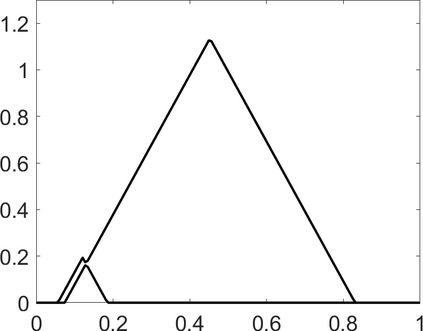
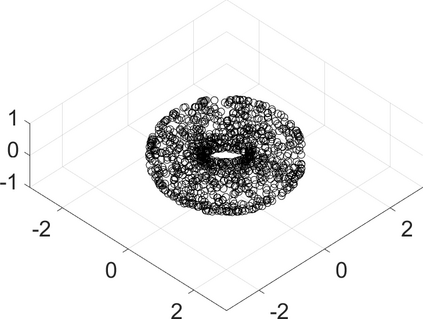
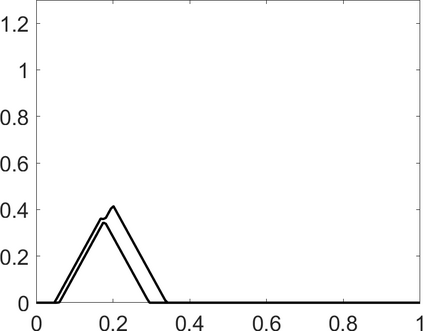
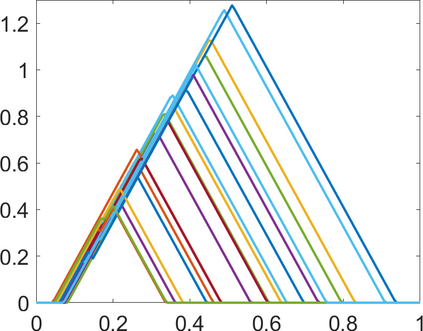
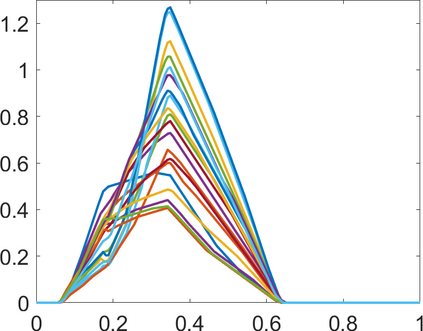
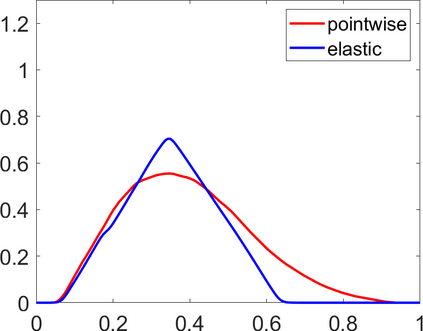
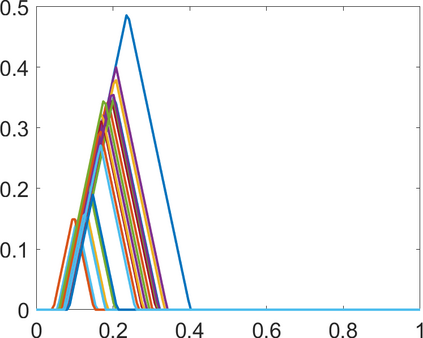
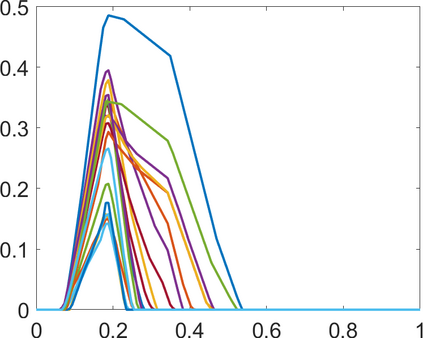
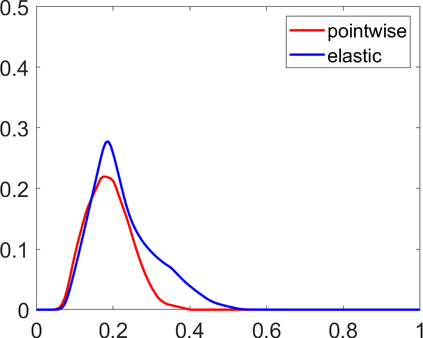
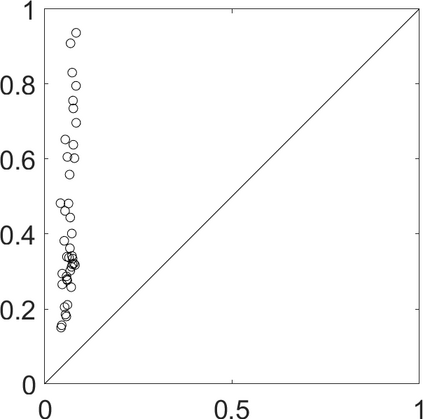
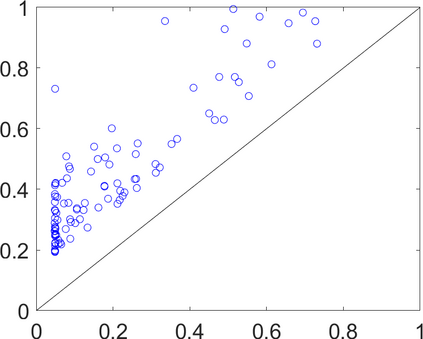
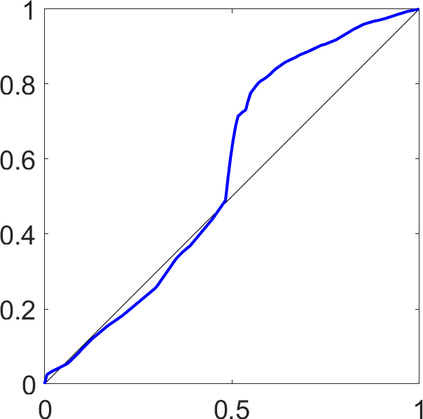
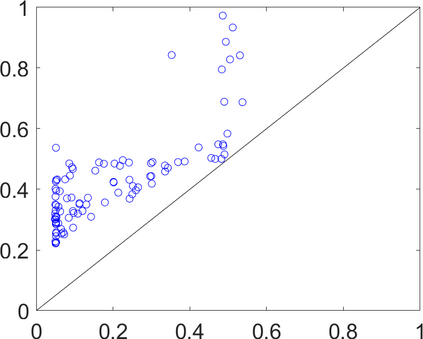
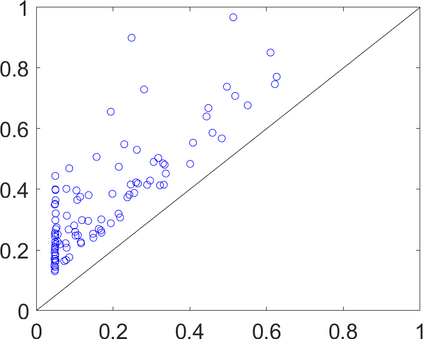
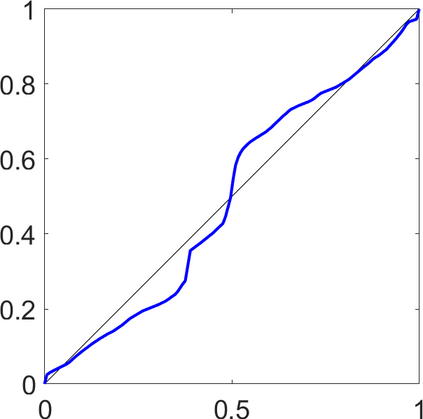
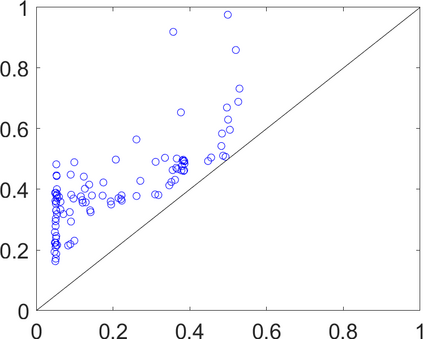
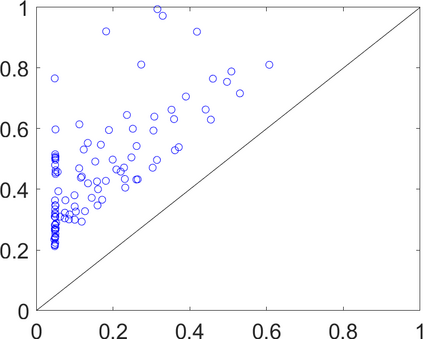
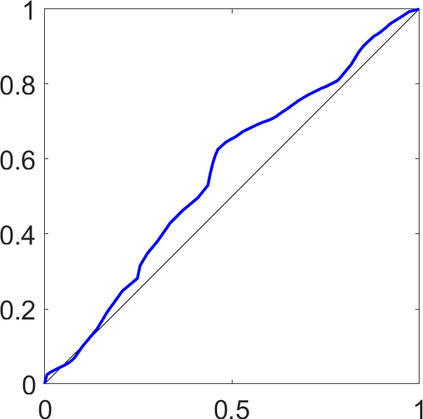
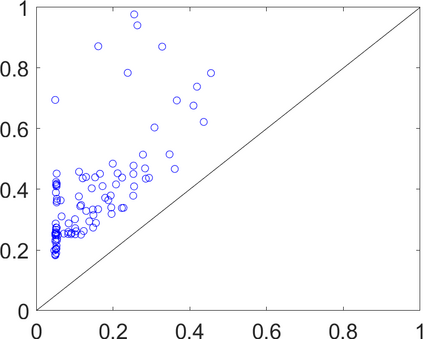
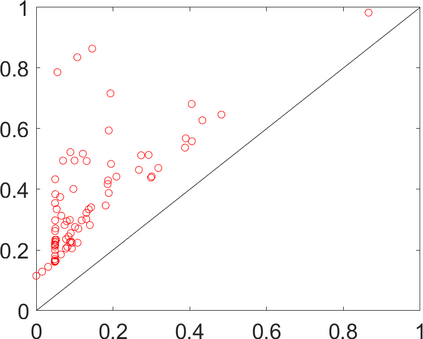
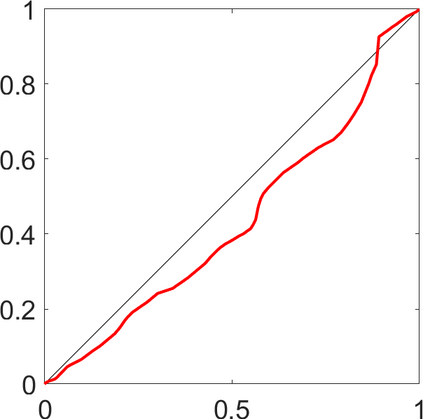
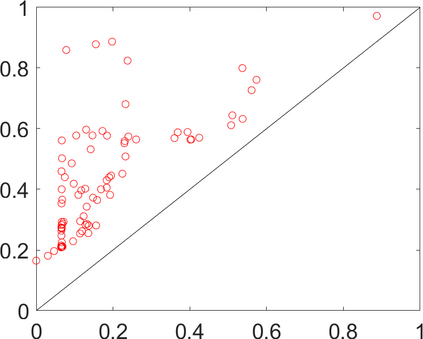
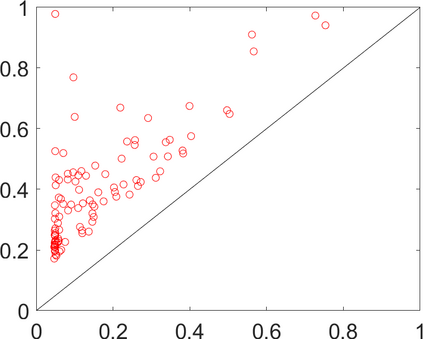
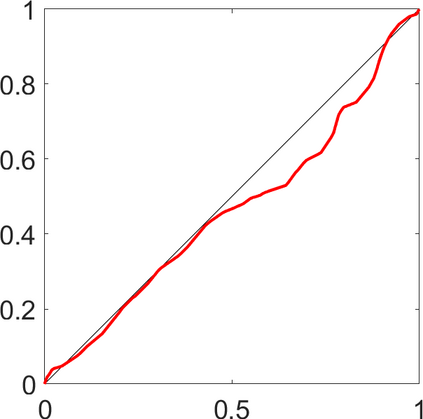
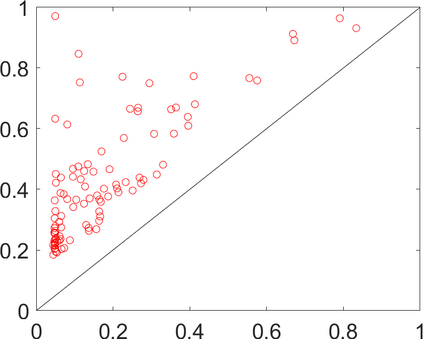
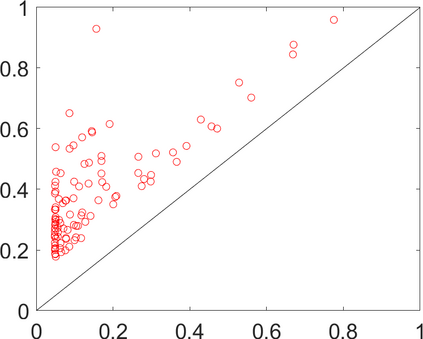
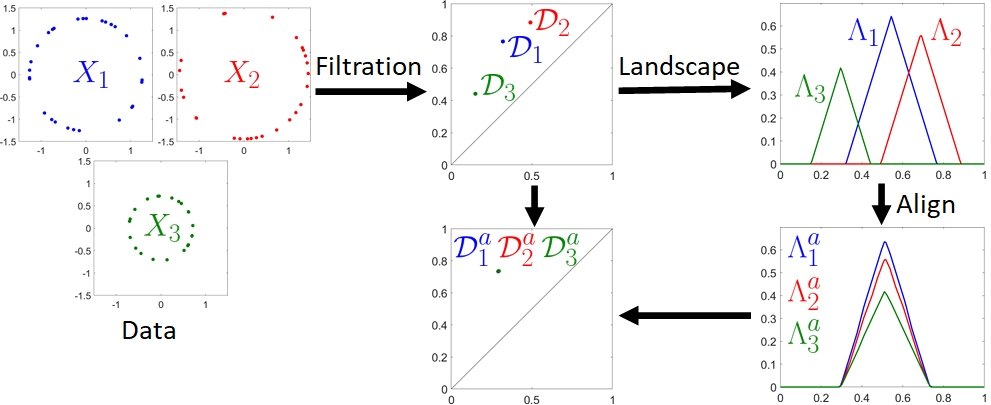
Persistence landscapes are functional summaries of persistence diagrams designed to enable analysis of the diagrams using tools from functional data analysis. They comprise a collection of scalar functions such that birth and death times of topological features in persistence diagrams map to extrema of functions and intervals where they are non-zero. As a consequence, topological information is encoded in both amplitude and phase components of persistence landscapes. Through functional data analysis of persistence landscapes under an elastic Riemannian metric, we show how meaningful statistical summaries of persistence landscapes (e.g., mean, dominant directions of variation) can be obtained by decoupling topological signal present in amplitude and phase variations. The estimated phase functions are tied to the resolution parameter that determines the filtration of simplicial complexes used to construct persistence diagrams. For a dataset obtained under scale and sampling variabilities, the phase function prescribes an optimal rate of increase of the resolution parameter for enhancing the topological signal in a persistence diagram. We demonstrate benefits of alignment through several simulation examples and a real data example concerning structure of brain artery trees represented as 3D point clouds.