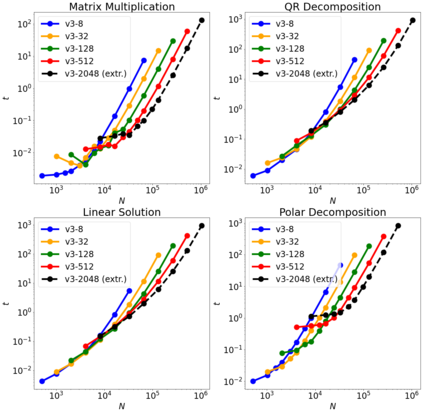
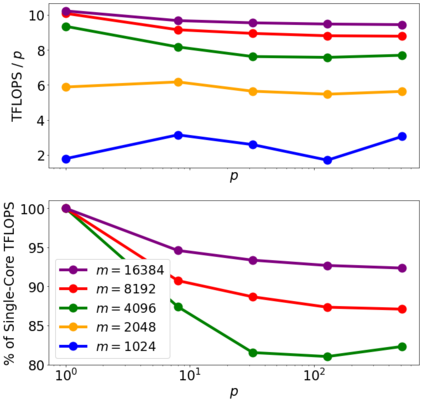
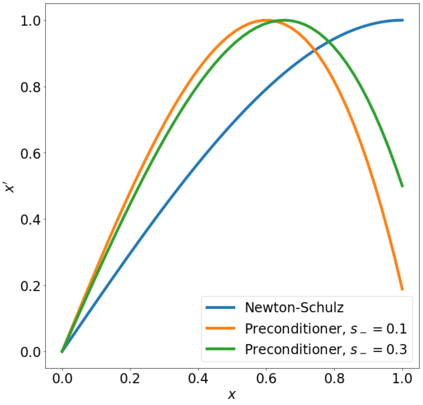
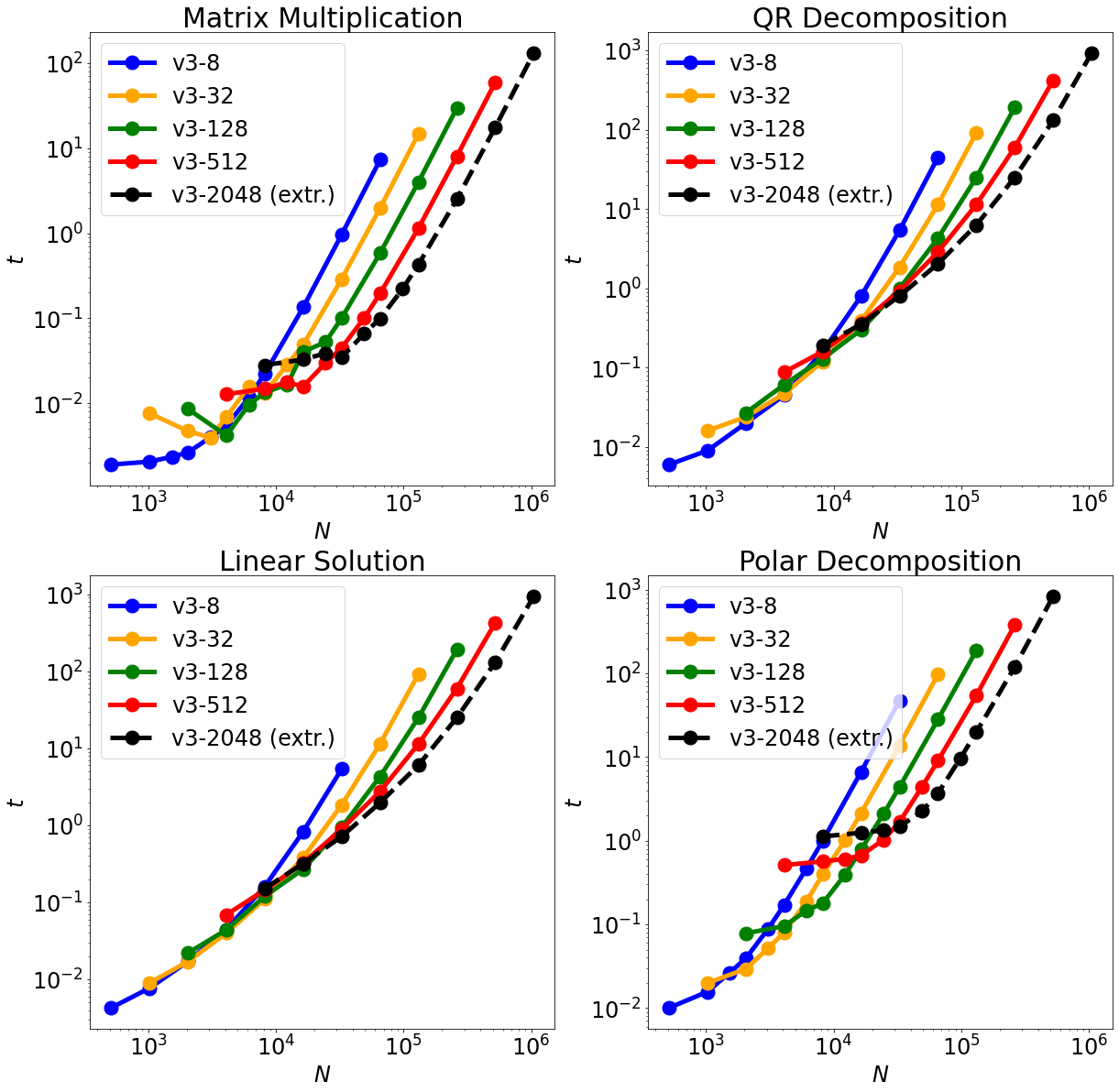
We have repurposed Google Tensor Processing Units (TPUs), application-specific chips developed for machine learning, into large-scale dense linear algebra supercomputers. The TPUs' fast inter-core interconnects (ICI)s, physically two-dimensional network topology, and high-bandwidth memory (HBM) permit distributed matrix multiplication algorithms to rapidly become computationally bound. In this regime, the matrix-multiply units (MXU)s dominate the runtime, yielding impressive scaling, performance, and raw size: operating in float32 precision, a full 2048-core pod of third generation TPUs can multiply two matrices with linear size $N= 220= 1 048 576$ in about 2 minutes. Via curated algorithms emphasizing large, single-core matrix multiplications, other tasks in dense linear algebra can similarly scale. As examples, we present (i) QR decomposition; (ii) resolution of linear systems; and (iii) the computation of matrix functions by polynomial iteration, demonstrated by the matrix polar factorization.
翻译:我们重新将谷歌Tensor处理器(TPUs)重新定位为用于机器学习的特定应用芯片,用于大规模密集线性代数超级计算机。TPU的快速核心间连接(ICI),物理二维网络地形学和高带宽内存(HBM)使得分布式矩阵倍增算法能够迅速在计算上捆绑起来。在这个制度中,矩阵多功能单位(MXU)在运行时占据主导位置,产生令人印象深刻的缩放、性能和原始大小:在浮点32精确度下运行,第三代TPU的整整2048核心芯粒可以在大约2分钟内乘以线性大小为220N=1 048 576美元的两个矩阵。Viaculate 算法强调大型、单一核心矩阵倍增,密度直线性代数中的其他任务也可以同样规模。举例说,我们提出了(i) QR 解剖;(ii) 线性系统的分辨率;以及(iii) 矩阵极分化所显示的矩阵函数的矩阵函数的计算。