Optimal Clearing Payments in a Financial Contagion Model

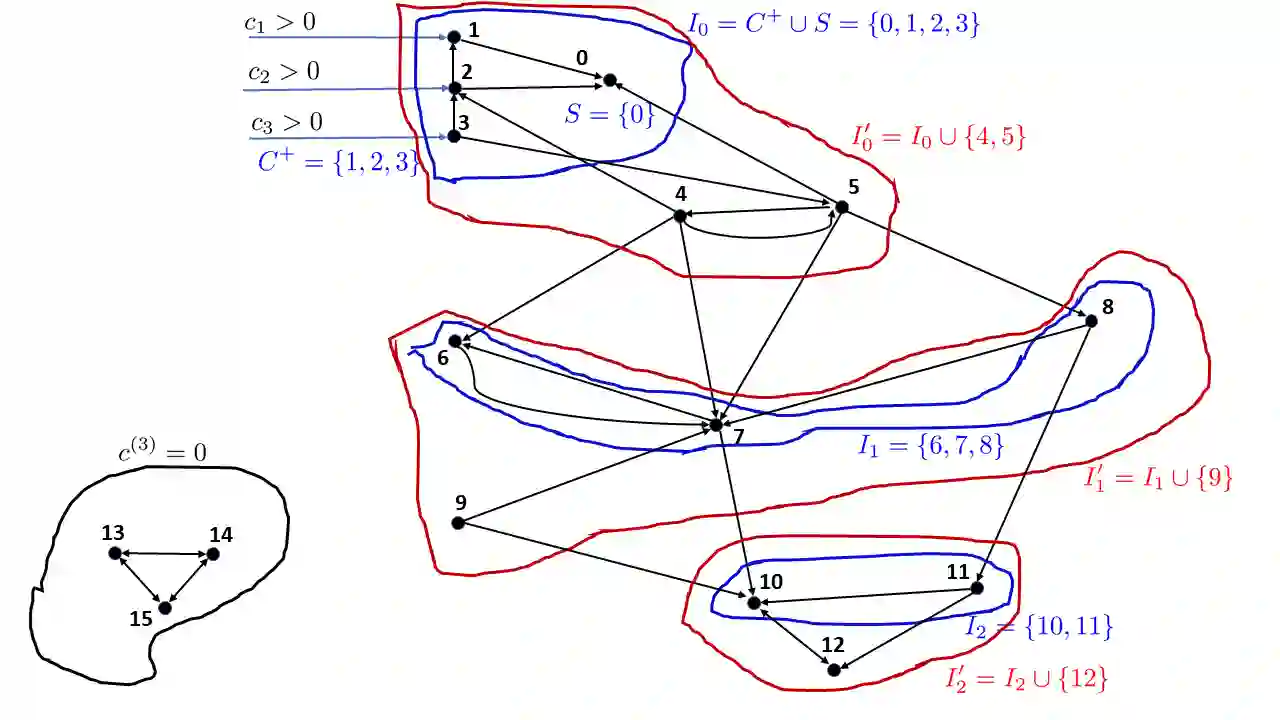
Modern financial networks are characterized by complex structures of mutual obligations. Such interconnections may propagate and amplificate individual defaults, leading in some cases to financial disaster. For this reason, mathematical models for the study and control of systemic risk (the risk of severe instabilities on the system as a whole, due to default of single entities) have attracted considerable research attention in recent years. One important line of research is concerned with mechanisms of clearing, that is, the mechanism by which mutual debts are repaid, in the regular regime, or in a default regime. One of the first models of a clearing mechanism was proposed by Eisenberg and Noe and is based on the three rules: limited liability, the priority of debt claims over the shareholders' interests, and the equal priority of debts (pro-rata rule). These three principles naturally lead to the concept of clearing vector (the vector of the entities' total payments). In this paper, we propose a necessary and sufficient condition for the uniqueness of clearing vector applicable to an arbitrary topology of the financial network. Further, we show that the overall system loss can be reduced if one relaxes the pro-rata rule and replaces the clearing vector by a matrix of clearing payments. This approach shifts the focus from the individual interest to the system, or social, interest, in order to control and contain the adverse effects of cascaded failures.