HaarPooling: Graph Pooling with Compressive Haar Basis

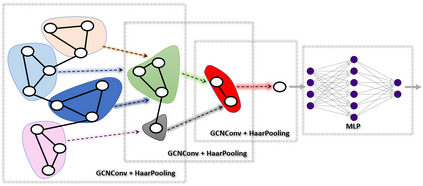
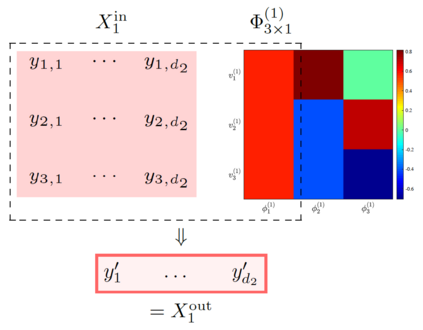
Deep Graph Neural Networks (GNNs) are instrumental in graph classification and graph-based regression tasks. In these tasks, graph pooling is a critical ingredient by which GNNs adapt to input graphs of varying size and structure. We propose a new graph pooling operation based on compressive Haar transforms, called HaarPooling. HaarPooling is computed following a chain of sequential clusterings of the input graph. The input of each pooling layer is transformed by the compressive Haar basis of the corresponding clustering. HaarPooling operates in the frequency domain by the synthesis of nodes in the same cluster and filters out fine detail information by compressive Haar transforms. Such transforms provide an effective characterization of the data and preserve the structure information of the input graph. By the sparsity of the Haar basis, the computation of HaarPooling is of linear complexity. The GNN with HaarPooling and existing graph convolution layers achieves state-of-the-art performance on diverse graph classification problems.