Flip Paths Between Lattice Triangulations

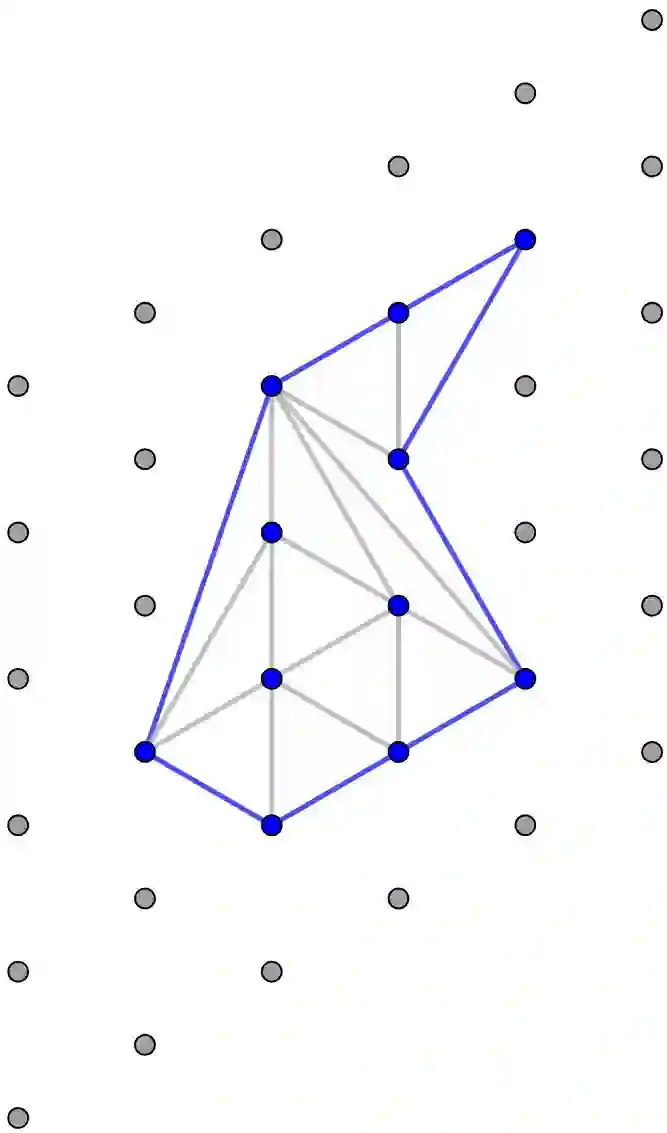
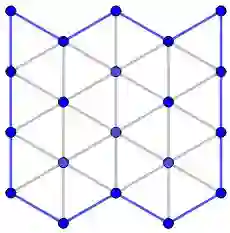
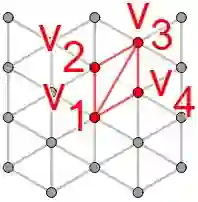
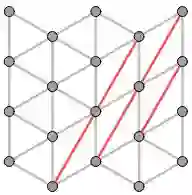
The problem of finding a diagonal \emph{flip} path between two triangulations has been studied for nearly a century. In the geometric setting, finding a flip path between two triangulations containing the minimum number of flips is NP-complete. However, for minimum flip paths between lattice triangulations, Eppstein and Caputo et al. gave algorithms running in $O\left(n^2\right)$ time, where $n$ is the number of points in the point-set. Eppstein proved this result for lattice point-sets bounded by convex polygons. Caputo et al. extended this result to the cases of non-convex bounding polygons and constrained flip paths that preserve a set of edges. In fact, Eppstein's approach readily extends to both cases. Our first result shows that there is a unique, partially-ordered set of flips whose valid linear-orderings are exactly the constrained, minimum flip paths between two lattice triangulations, leading to an algorithm to compute such a minimum flip path in $O\left(n^{\frac{3}{2}}\right)$ time. As a further improvement over previous results, in many natural cases, our algorithm runs in time linear in the length of the minimum flip path. Our second result characterizes pairs of triangulations $T$ and $T'$ that contain given sets of edges $G$ and $G'$ respectively, and attain the minimum flip path between each other, where the minimum is taken over such pairs of triangulations. Finally, we demonstrate how our results can model crack propagation in crystalline materials caused by Stone-Wales defects. Notably, the above results follow from simple number-theoretic and geometric concepts.