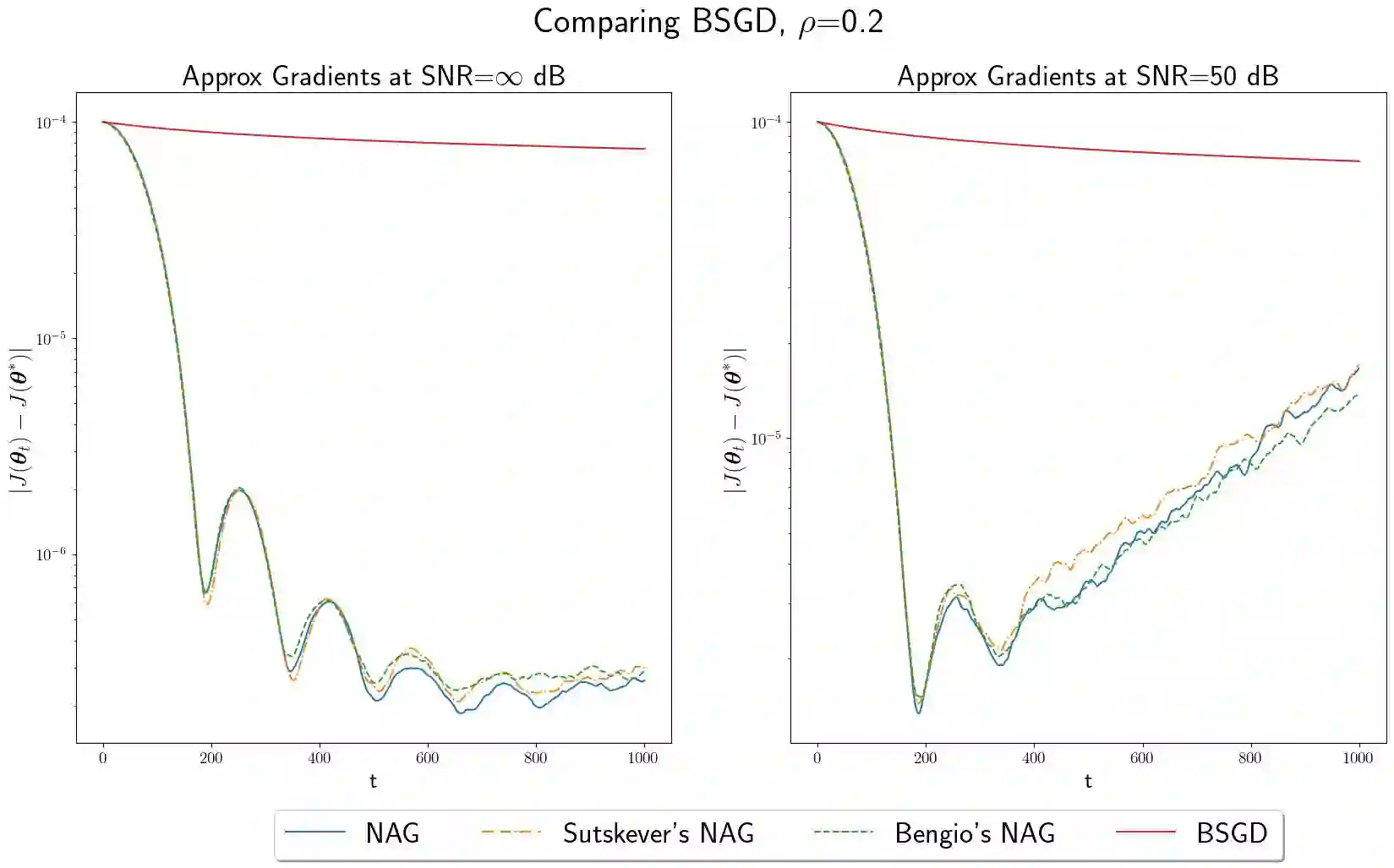
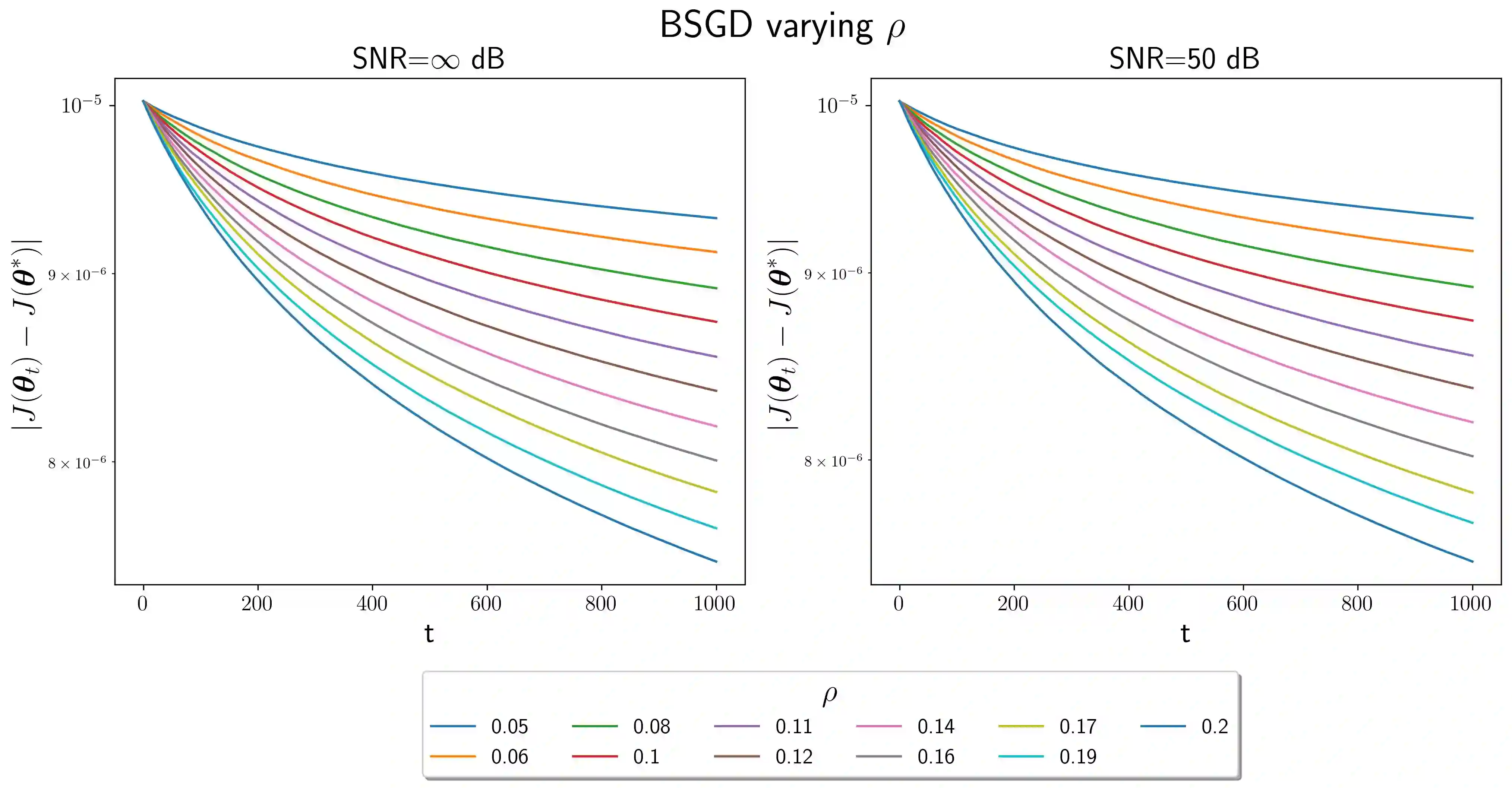
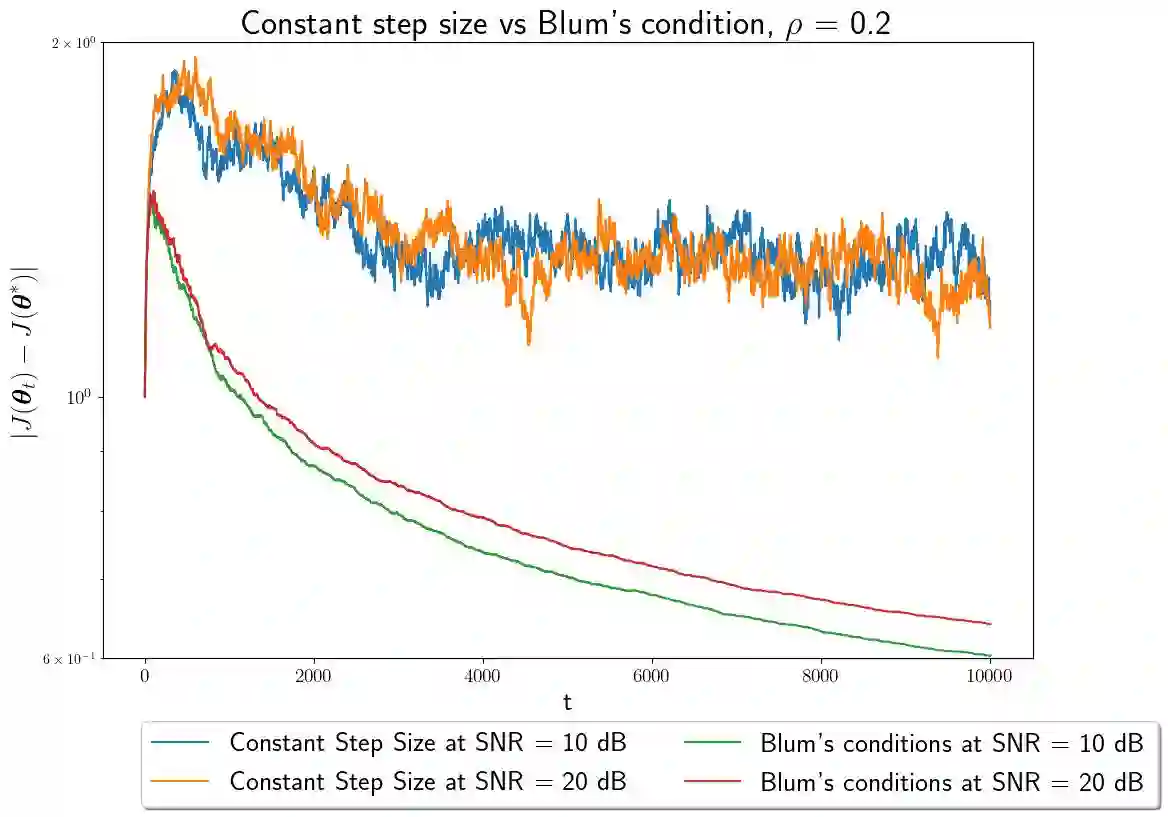
In this paper, we study convex optimization using a very general formulation called BSGD (Block Stochastic Gradient Descent). At each iteration, some but not necessary all components of the argument are updated. The direction of the update can be one of two possibilities: (i) A noise-corrupted measurement of the true gradient, or (ii) an approximate gradient computed using a first-order approximation, using function values that might themselves be corrupted by noise. This formulation embraces most of the currently used stochastic gradient methods. We establish conditions for BSGD to converge to the global minimum, based on stochastic approximation theory. Then we verify the predicted convergence through numerical experiments. Out results show that when approximate gradients are used, BSGD converges while momentum-based methods can diverge. However, not just our BSGD, but also standard (full-update) gradient descent, and various momentum-based methods, all converge, even with noisy gradients.
翻译:在本文中,我们使用一种非常笼统的配方BSGD (Block Stochastistic Gradient Emple) 来研究 convex 优化。 每次迭代时,都会更新所有参数的有些部分,但并非必要。更新的方向可以是两种可能性之一:(一) 对真实梯度进行噪音干扰的测量,或(二) 使用一阶近似值计算大约的梯度,使用可能因噪音而腐蚀的函数值。这种配方包含目前使用的多数随机梯度方法。我们根据随机近似理论,为BSGD达到全球最小值创造了条件。然后我们通过数字实验来核查预测的趋同。结果显示,当使用近似梯度时,BSGD会聚集,而以动力为基础的方法会有所不同。然而,不仅我们的BSGD(全新)梯度梯度,而且标准(全新)梯度梯度的梯度下,以及各种以动力为基础的方法也会趋同,即使与噪音梯度相趋同。