Nested $\hat R$: Assessing Convergence for Markov chain Monte Carlo when using many short chains

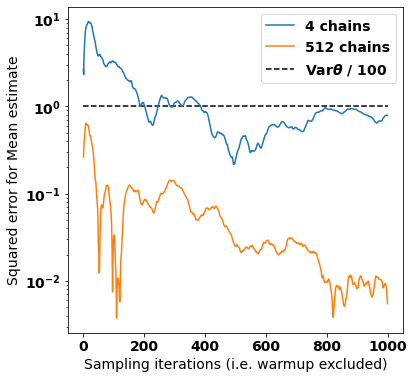
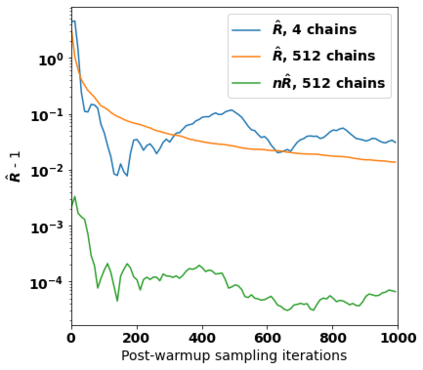
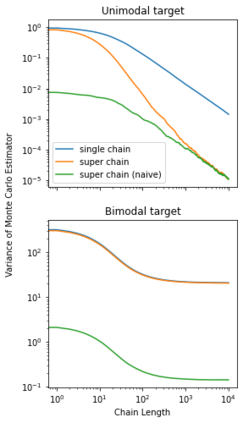
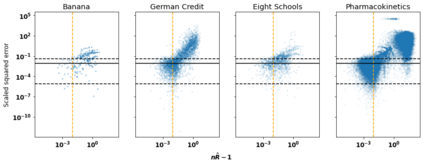
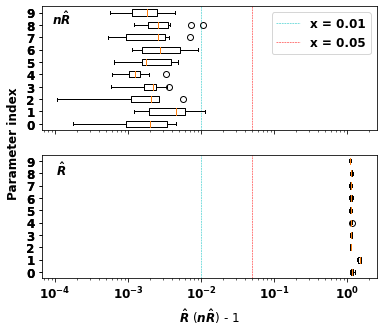
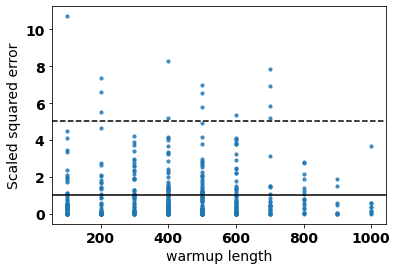
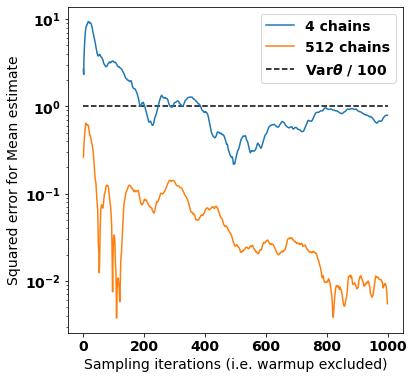
When using Markov chain Monte Carlo (MCMC) algorithms, we can increase the number of samples either by running longer chains or by running more chains. Practitioners often prefer the first approach because chains need an initial ``warmup'' phase to forget their initial states; the number of operations needed for warmup is constant with respect to chain length but increases linearly with the number of chains. However, highly parallel hardware accelerators such as GPUs may allow us to run many chains in parallel almost as quickly as a single chain. This makes it more attractive to run many chains with a short sampling phase. Unfortunately, existing diagnostics are not designed for the ``many short chains'' regime. This is notably the case for the popular $\hat R$ statistic which claims convergence only if the effective sample size \textit{per chain} is sufficiently large. We present $\mathfrak n\hat R$, a generalization of $\hat R$, which does not conflate short chains and poor mixing, and offers a useful diagnostic provided we run enough chains and meet certain initialization conditions. We define what constitutes a proper warmup in the many-chains regime and recommend a threshold for $\mathfrak n \hat R$. Furthermore we use $\mathfrak n \hat R$ to construct a warmup scheme with an adaptive length, allowing users to avoid running their MCMC algorithms longer than necessary.