Sparse random hypergraphs: Non-backtracking spectra and community detection

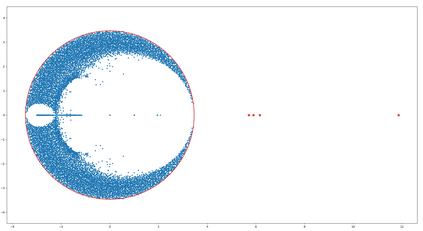
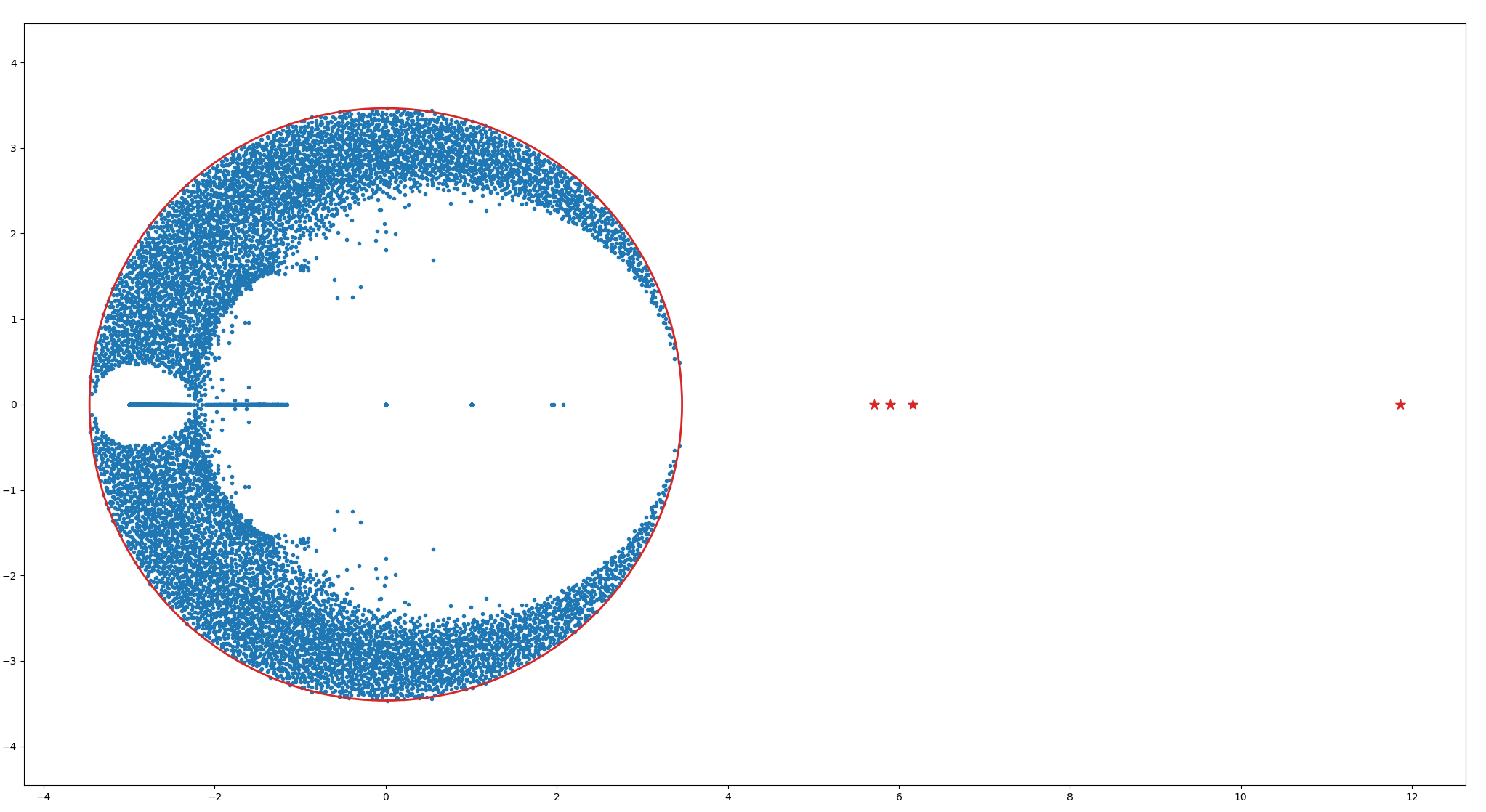
We consider the community detection problem in a sparse $q$-uniform hypergraph $G$, assuming that $G$ is generated according to the so-called Hypergraph Stochastic Block Model (HSBM). We prove that a spectral method based on the non-backtracking operator for hypergraphs works with high probability down to the generalized Kesten-Stigum detection threshold conjectured by Angelini et al. We characterize the spectrum of the non-backtracking operator for the sparse HSBM, and provide an efficient dimension reduction procedure using the Ihara-Bass formula for hypergraphs. As a result, community detection for the sparse HSBM on $n$ vertices can be reduced to an eigenvector problem of a $2n\times 2n$ non-normal matrix constructed from the adjacency matrix and the degree matrix of the hypergraph. To the best of our knowledge, this is the first provable and efficient spectral algorithm that achieves the conjectured threshold for HSBMs with $k$ blocks generated according to a general symmetric probability tensor.