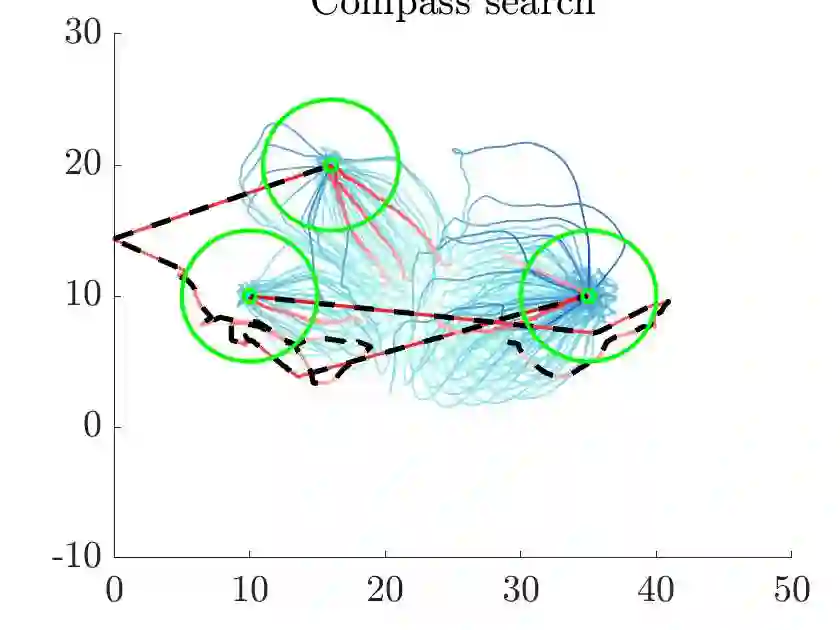
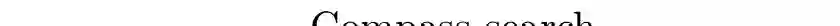领导人在多处撤离的未知环境中进行人群疏散的最佳战略 (Optimized leaders strategies for crowd evacuation in unknown environments with multiple exits)

In this chapter, we discuss the mathematical modeling of egressing pedestrians in an unknown environment with multiple exits. We investigate different control problems to enhance the evacuation time of a crowd of agents, by few informed individuals, named leaders. Leaders are not recognizable as such and consist of two groups: a set of unaware leaders moving selfishly toward a fixed target, whereas the rest is coordinated to improve the evacuation time introducing different performance measures. Follower-leader dynamics is initially described microscopically by an agent-based model, subsequently a mean-field type model is introduced to approximate the large crowd of followers. The mesoscopic scale is efficiently solved by a class of numerical schemes based on direct simulation Monte-Carlo methods. Optimization of leader strategies is performed by a modified compass search method in the spirit of metaheuristic approaches. Finally, several virtual experiments are studied for various control settings and environments.

翻译：在本章中,我们讨论在具有多个出口的未知环境中行人出行行行行人数学模型的数学模型。我们调查不同的控制问题,以通过少数知情的个人、被点名的领导人来增加一批代理人的疏散时间。领导人无法被认出,他们由两组人组成:一组不知名的领导人自私地走向固定目标,而其余的则协调起来,以改进采用不同性能措施的疏散时间。最初,以代理为基础的模型对随行者-领导动态进行微缩描述,随后,引入了一种中位型模型,以接近众多的追随者。中位数比例通过基于直接模拟蒙特-卡洛方法的一组数字计划来有效解决。领导者战略的优化是本着美经主义精神,以修改的罗盘搜索方法进行的。最后,为各种控制环境和环境研究了若干虚拟实验。