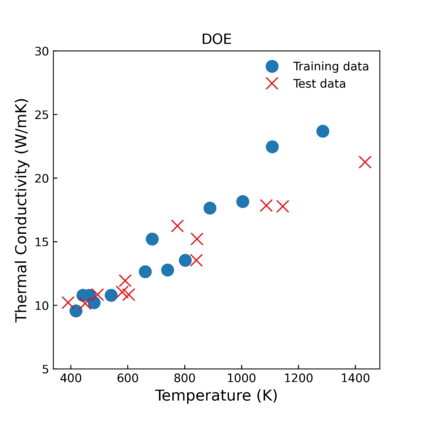
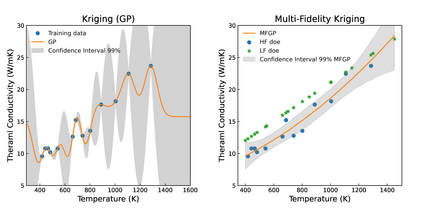
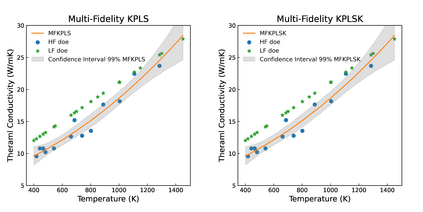
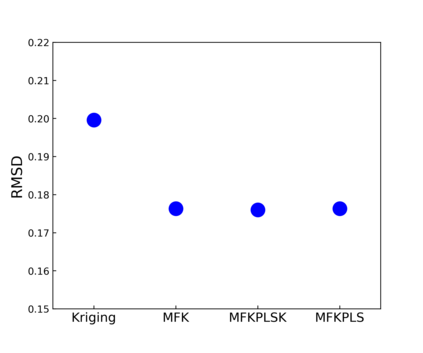
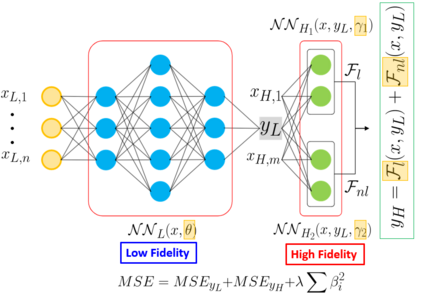
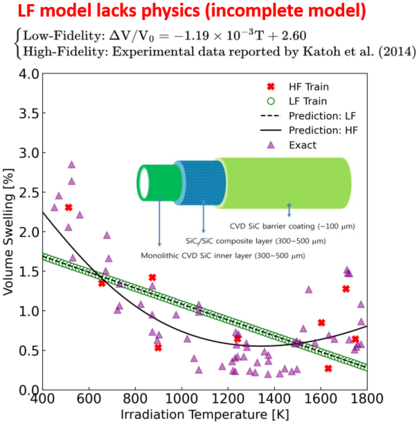
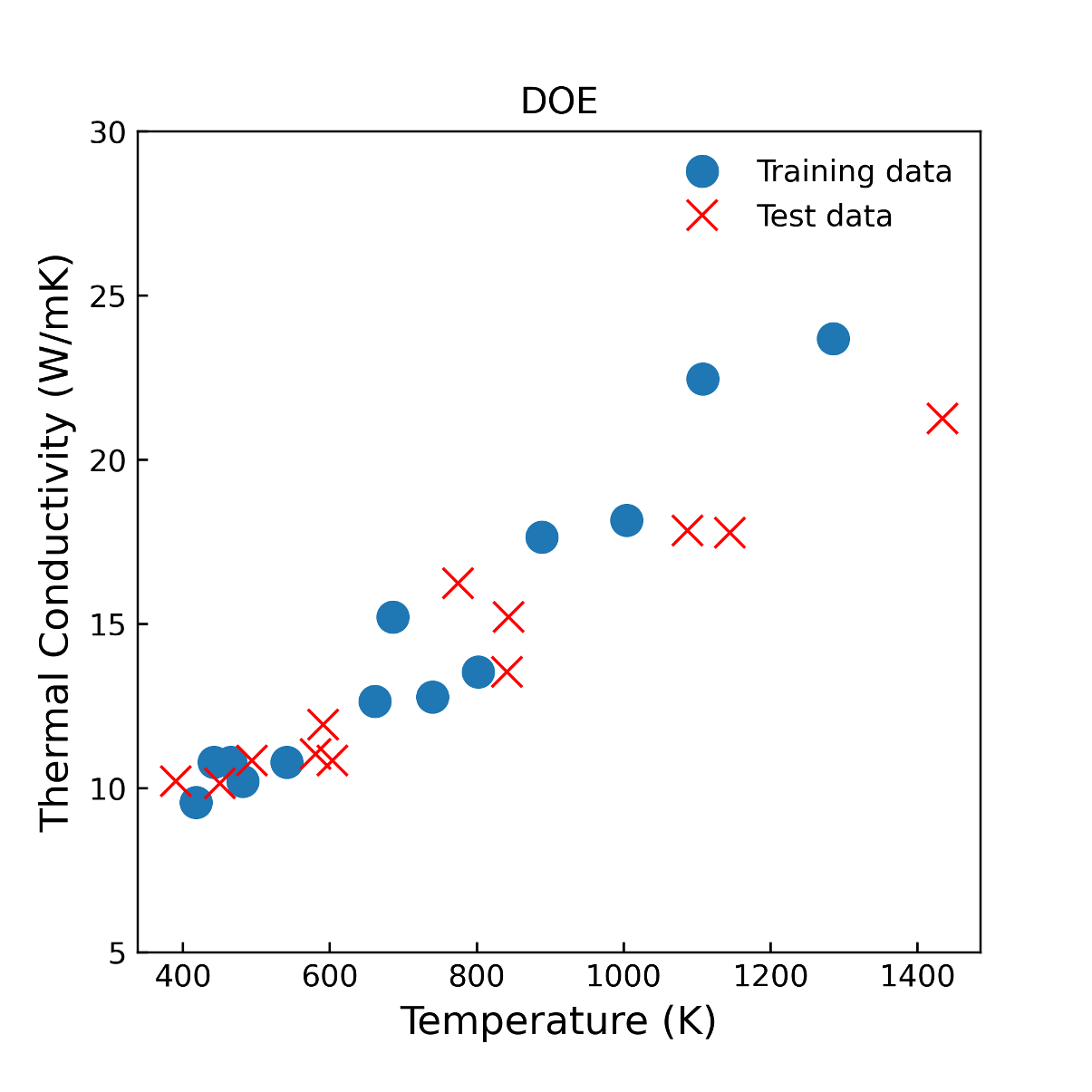
The Gaussian Process (GP)-based surrogate model has the inherent capability of capturing the anomaly arising from limited data, lack of data, missing data, and data inconsistencies (noisy/erroneous data) present in the modeling and simulation component of the digital twin framework, specifically for the accident tolerant fuel (ATF) concepts. However, GP will not be very accurate when we have limited high-fidelity (experimental) data. In addition, it is challenging to apply higher dimensional functions (>20-dimensional function) to approximate predictions with the GP. Furthermore, noisy data or data containing erroneous observations and outliers are major challenges for advanced ATF concepts. Also, the governing differential equation is empirical for longer-term ATF candidates, and data availability is an issue. Physics-informed multi-fidelity Kriging (MFK) can be useful for identifying and predicting the required material properties. MFK is particularly useful with low-fidelity physics (approximating physics) and limited high-fidelity data - which is the case for ATF candidates since there is limited data availability. This chapter explores the method and presents its application to experimental thermal conductivity measurement data for ATF. The MFK method showed its significance for a small number of data that could not be modeled by the conventional Kriging method. Mathematical models constructed with this method can be easily connected to later-stage analysis such as uncertainty quantification and sensitivity analysis and are expected to be applied to fundamental research and a wide range of product development fields. The overarching objective of this chapter is to show the capability of MFK surrogates that can be embedded in a digital twin system for ATF.
翻译:以 Gausian 进程为基础的代金模型具有内在能力,能够捕捉数字双框架模型和模拟部分中存在的数据、数据缺乏、数据缺失和数据不一致(noisy/erroneous data)产生的异常现象,特别是对于事故容忍燃料(ATF)概念而言。然而,当我们限制高不全度(实验性)数据时,Gausian 替代模型将不十分准确。此外,运用高维功能( > 20维总体功能)来与GP相近的预测。此外,包含错误观测和异常数据的数据噪音或数据是高级ATF概念概念的主要挑战。此外,对长期ATF候选者来说,管理差异方程式是实验性的,数据可用性方程是一个问题。物理知情性多维度克里金(MFK)模型可用于识别和预测所需物质特性。MFMK 低度物理学(应用20维度总体功能)和有限高度数据数据――对于ATF的基本数据应用者来说,是主要挑战性数据或异常性数据数据,因为这种数据分析是有限的双基数据方法,因此可以展示其常规数据方法。