A flexible split-step scheme for MV-SDEs

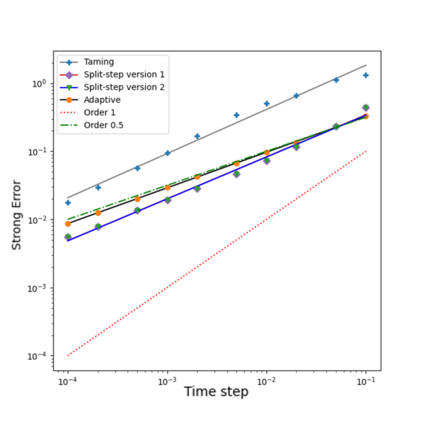
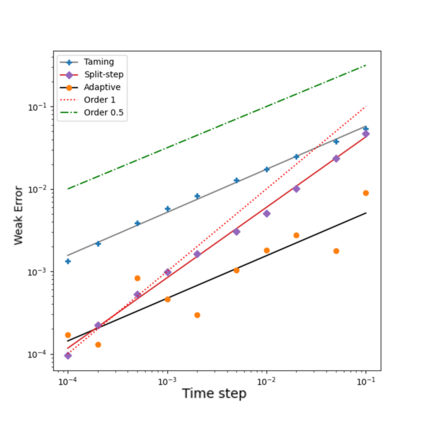
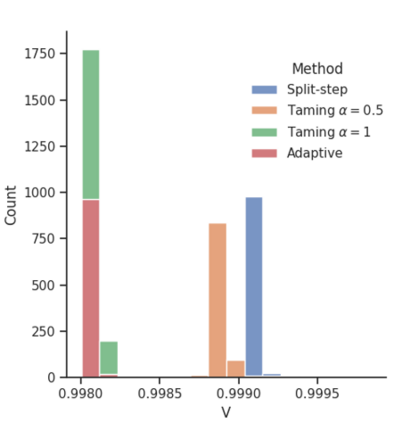
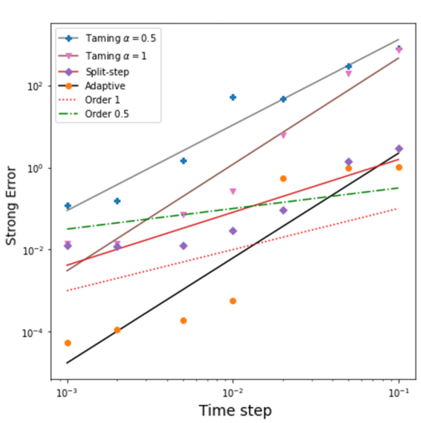
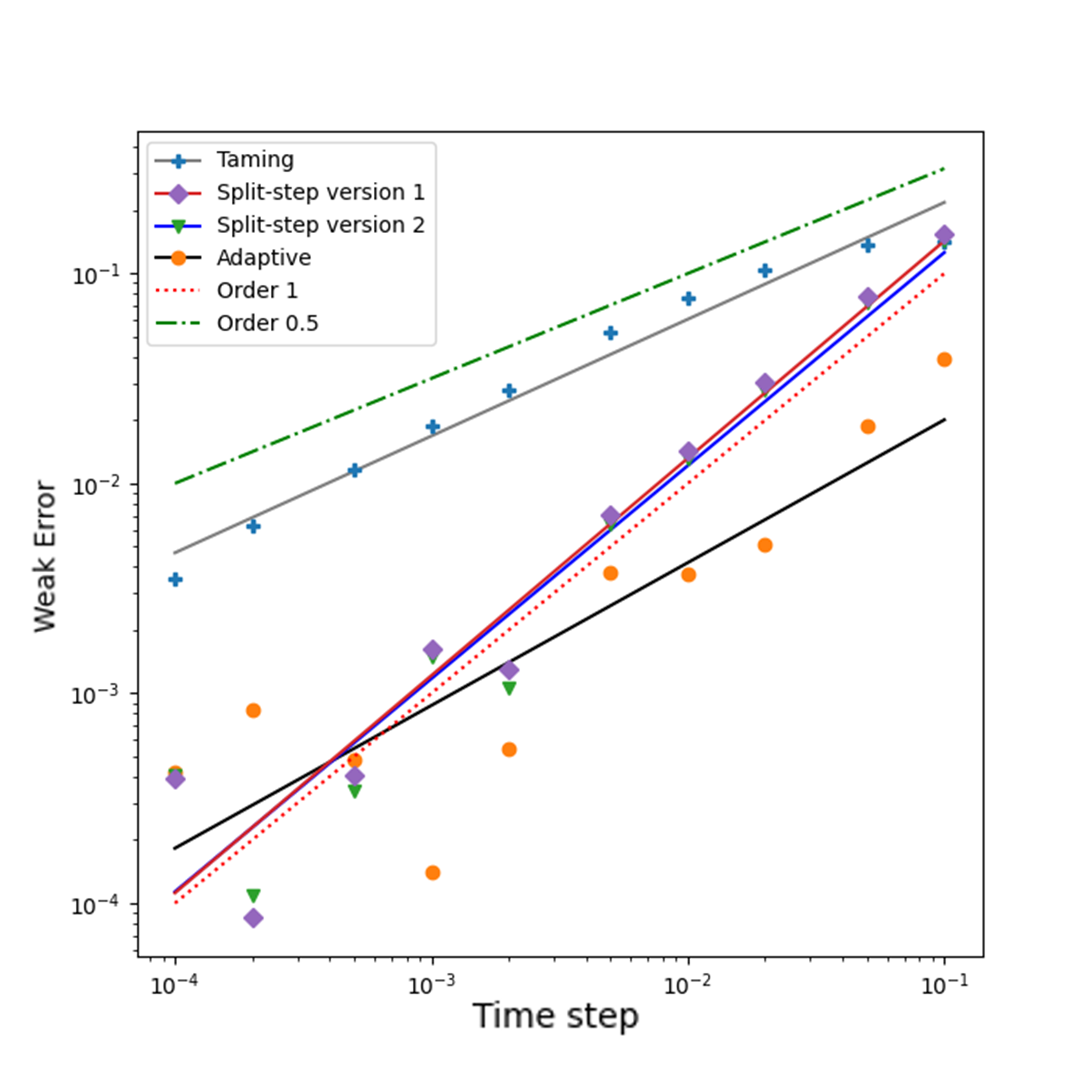
We present an implicit Split-Step explicit Euler type Method (dubbed SSM) for the simulation of McKean-Vlasov Stochastic Differential Equations (MV-SDEs) with drifts of superlinear growth in space, Lipschitz in measure and non-constant Lipschitz diffusion coefficient. The scheme is designed to leverage the structure induced by the interacting particle approximation system, including parallel implementation and the solvability of the implicit equation. The scheme attains the classical $1/2$ root mean square error (rMSE) convergence rate in stepsize and closes the gap left by [18, "Simulation of McKean-Vlasov SDEs with super-linear growth" in IMA Journal of Numerical Analysis, 01 2021. draa099] regarding efficient implicit methods and their convergence rate for this class of McKean-Vlasov SDEs. A sufficient condition for mean-square contractivity of the scheme is presented. Several numerical examples are presented, including a comparative analysis to other known algorithms for this class (Taming and Adaptive time-stepping) across parallel and non-parallel implementations.