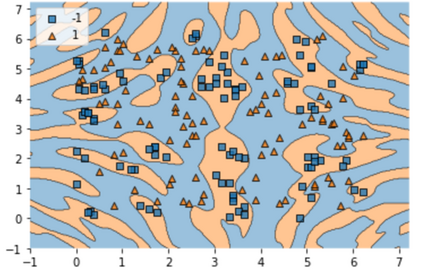
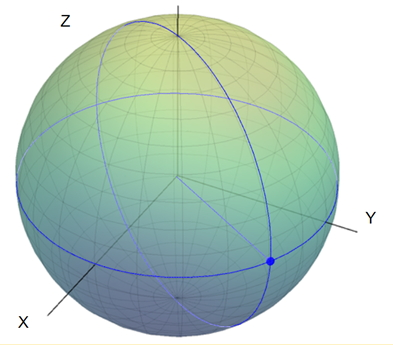
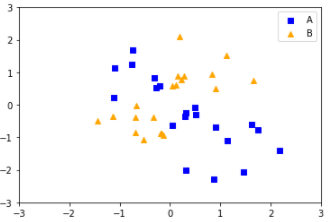
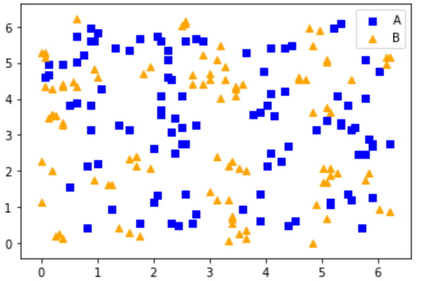
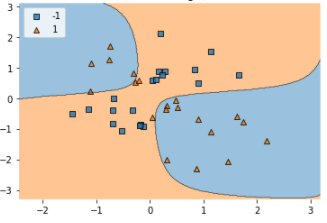
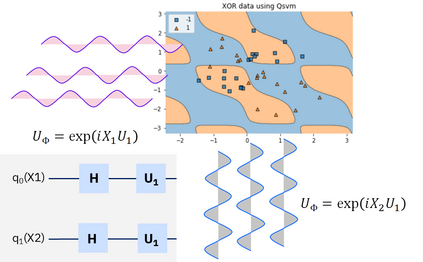
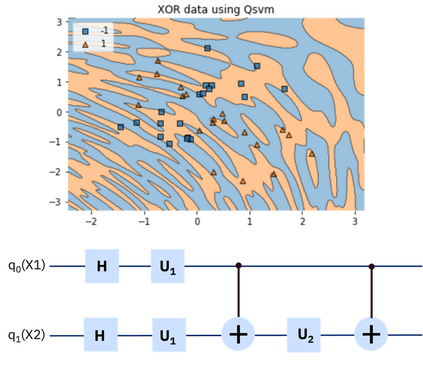
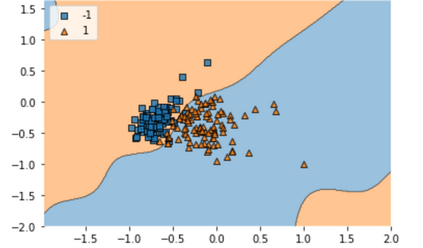
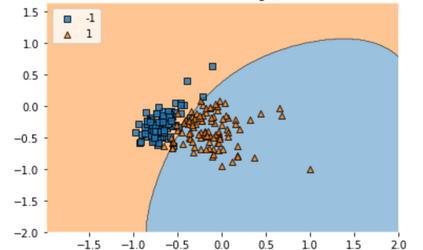
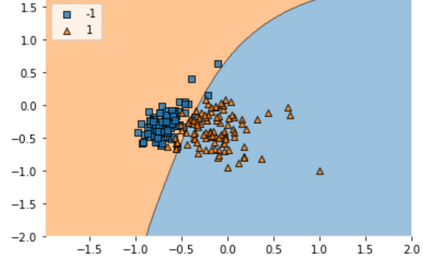
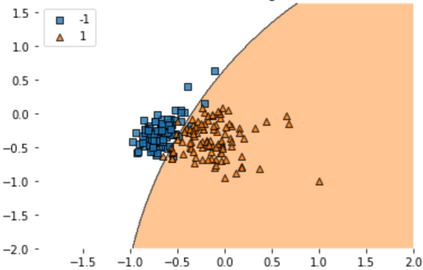
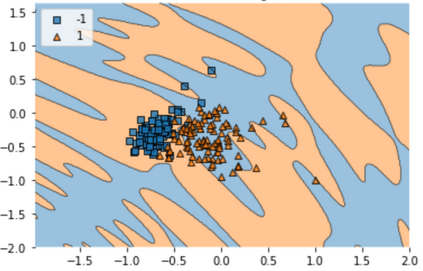
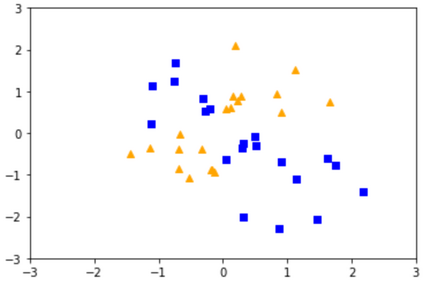
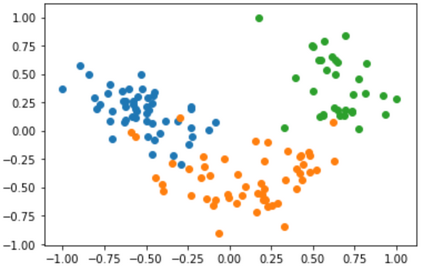
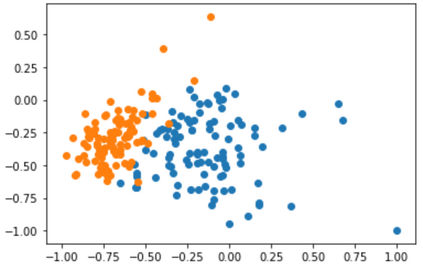
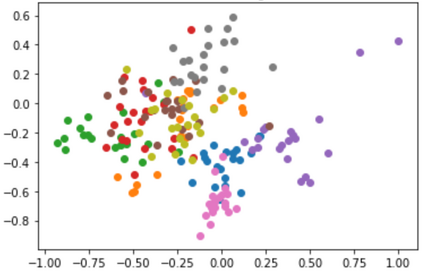
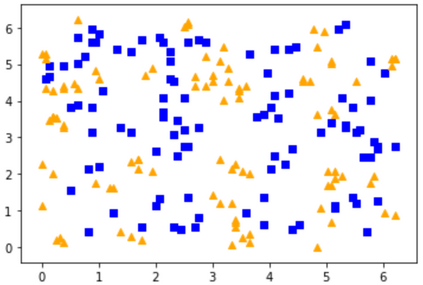
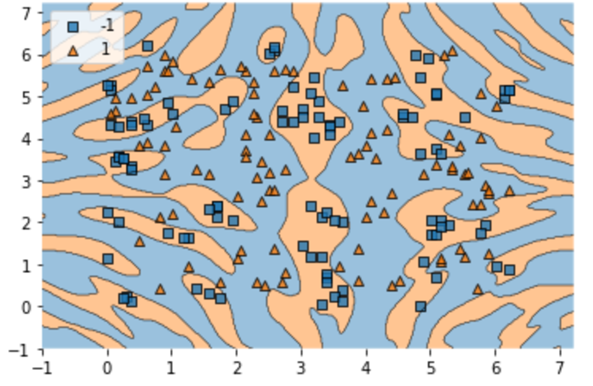
Quantum machine learning (QML) has emerged as an important area for Quantum applications, although useful QML applications would require many qubits. Therefore our paper is aimed at exploring the successful application of the Quantum Support Vector Machine (QSVM) algorithm while balancing several practical and technical considerations under the Noisy Intermediate-Scale Quantum (NISQ) assumption. For the quantum SVM under NISQ, we use quantum feature maps to translate data into quantum states and build the SVM kernel out of these quantum states, and further compare with classical SVM with radial basis function (RBF) kernels. As data sets are more complex or abstracted in some sense, classical SVM with classical kernels leads to less accuracy compared to QSVM, as classical SVM with typical classical kernels cannot easily separate different class data. Similarly, QSVM should be able to provide competitive performance over a broader range of data sets including ``simpler'' data cases in which smoother decision boundaries are required to avoid any model variance issues (i.e., overfitting). To bridge the gap between ``classical-looking'' decision boundaries and complex quantum decision boundaries, we propose to utilize general shallow unitary transformations to create feature maps with rotation factors to define a tunable quantum kernel, and added regularization to smooth the separating hyperplane model. We show in experiments that this allows QSVM to perform equally to SVM regardless of the complexity of the data sets and outperform in some commonly used reference data sets.
翻译:量子机器学习(QML)已经成为量子应用的一个重要领域,尽管有用的 QML 应用需要许多量子。 因此,我们的文件旨在探索量子支持矢量机(QSVM)算法的成功应用,同时平衡Noisy 中级量子(NISQ)假设下的若干实际考虑和技术考虑。对于NISQ下的量子SVM来说,我们使用量子特征地图将数据转换成量子状态,并将SVM 机库从这些量子状态中建立出SVM,并进一步与具有辐射基础功能的经典SVM 机库(RBF) 功能进行对比。由于数据集在某种意义上更为复杂或抽象,传统的SVM 机库与QSVM 假设下的一些实际考虑和技术考虑比较不那么精确。对于典型的典型的经典SVM 机库来说,我们使用量子图来提供更为广泛的高的性能, 包括VPorer Refer 数据 样式的精度参考, 和 直径基调的Sral-ralalalalalalalal 等数据, 范围需要使用某种模型, 等量级的精确的模型来解释。