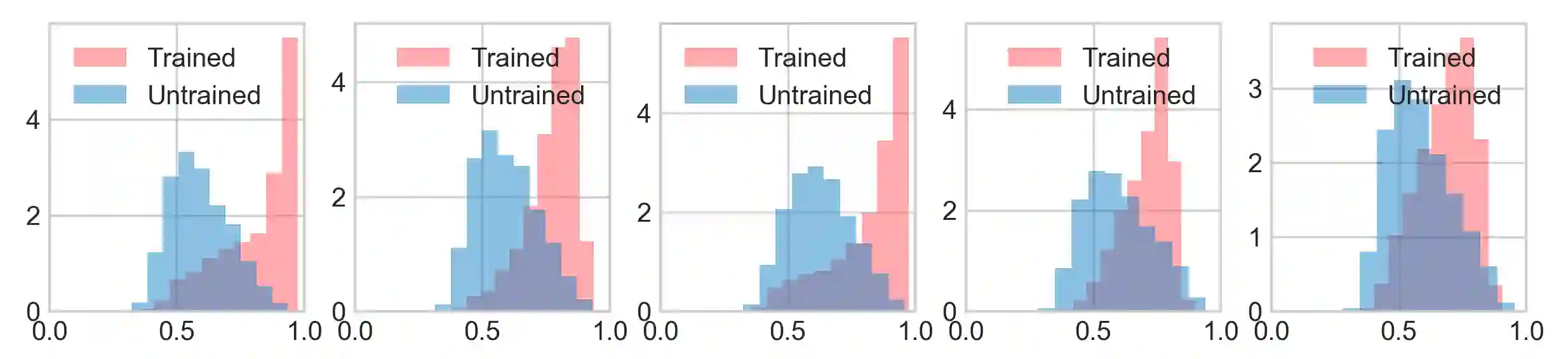
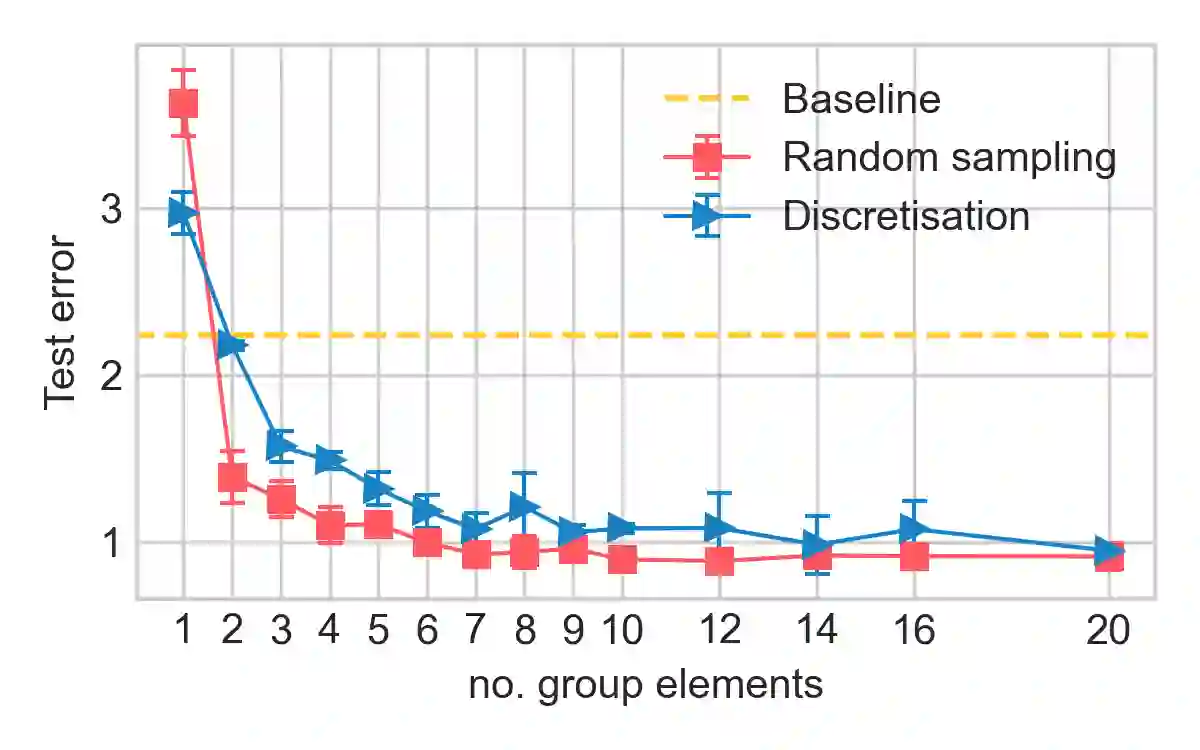
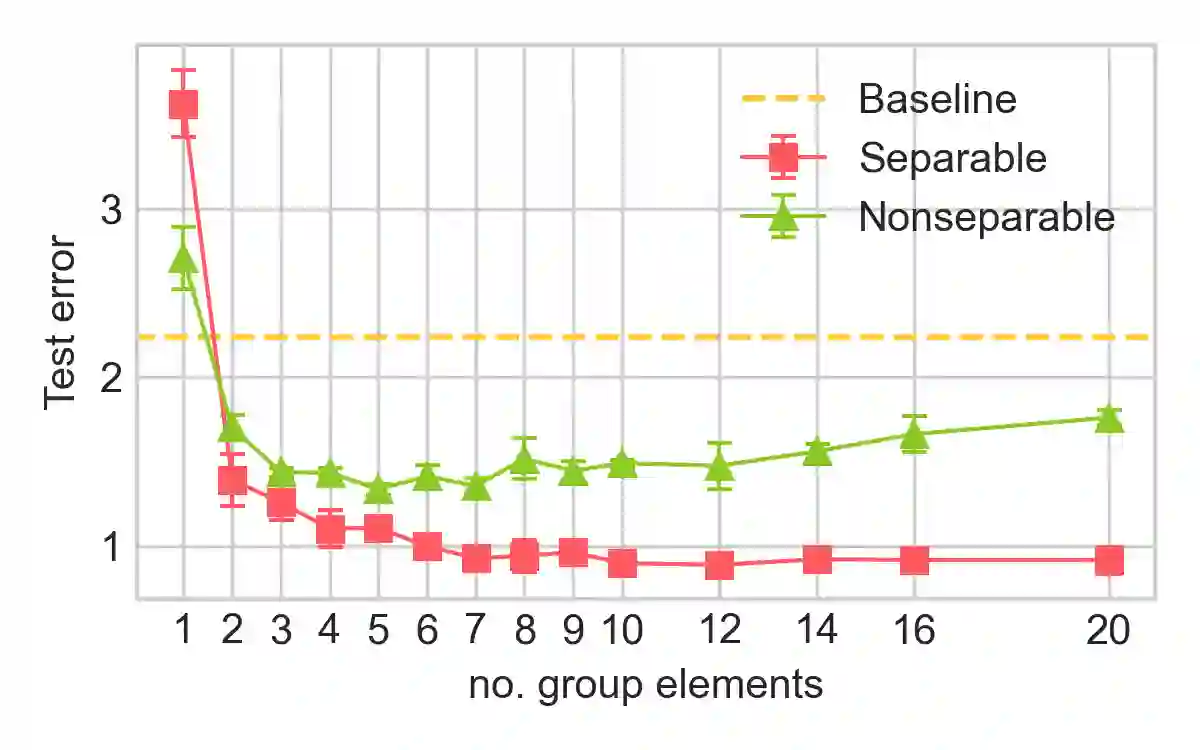
Group convolutional neural networks (G-CNNs) have been shown to increase parameter efficiency and model accuracy by incorporating geometric inductive biases. In this work, we investigate the properties of representations learned by regular G-CNNs, and show considerable parameter redundancy in group convolution kernels. This finding motivates further weight-tying by sharing convolution kernels over subgroups. To this end, we introduce convolution kernels that are separable over the subgroup and channel dimensions. In order to obtain equivariance to arbitrary affine Lie groups we provide a continuous parameterisation of separable convolution kernels. We evaluate our approach across several vision datasets, and show that our weight sharing leads to improved performance and computational efficiency. In many settings, separable G-CNNs outperform their non-separable counterpart, while only using a fraction of their training time. In addition, thanks to the increase in computational efficiency, we are able to implement G-CNNs equivariant to the $\mathrm{Sim(2)}$ group; the group of dilations, rotations and translations. $\mathrm{Sim(2)}$-equivariance further improves performance on all tasks considered.
翻译:群集神经网络( G- CNNs) 通过纳入几何感性偏差, 显示了提高参数效率和模型精度的参数效率。 在这项工作中, 我们调查了常规 G- CNNs 所学到的表达方式的特性, 并展示了群集共进内核中相当的参数冗余 。 这个发现通过在分组之间共享共进内核, 刺激了进一步的权重紧张。 为此, 我们引入了可分解于分组和频道维度的共进内核。 为了获得任意的亲近性组合的均匀性。 为了实现分化, 我们提供了分化内核内核的连续参数。 我们评估了我们在若干视觉数据集中学习的表达方式, 并显示我们的权重共享可以提高性能和计算效率 。 在许多环境中, 分化 G- CNs 超越其不可分离的对等值, 而只使用其培训时间的一小部分。 此外, 由于计算效率的提高, 我们能够执行 G- CNNs 等化到 $\ Sim} 所有考虑的任务的变换数组。