A fast algorithm for solving a three-dimensional inverse multiple frequency problems of scalar acoustics in a cylindrical region

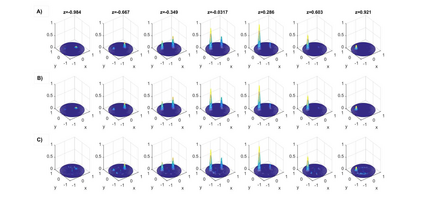
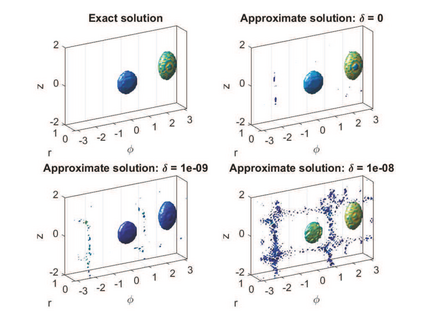
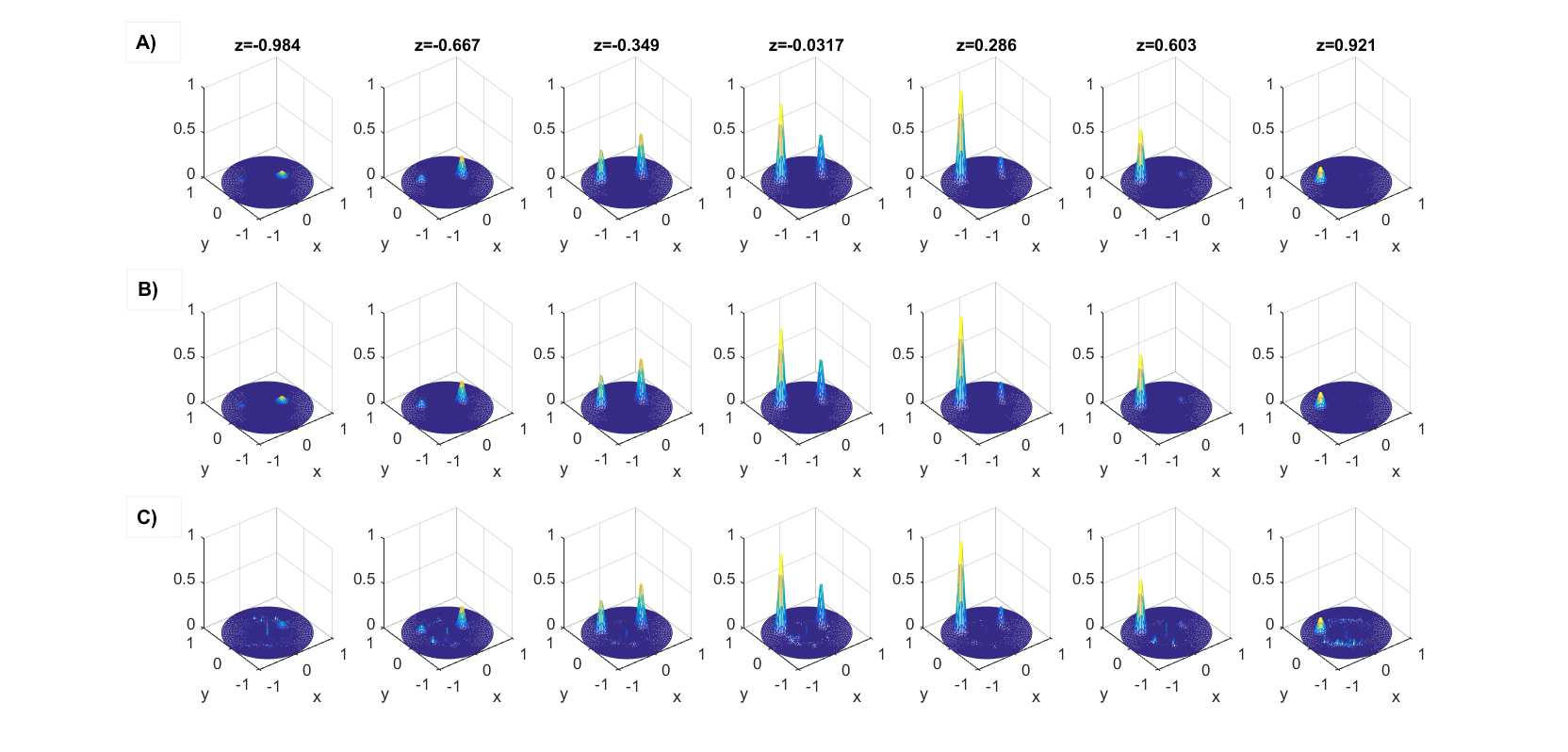
A new algorithm for the stable solution of a three-dimensional scalar inverse problem of acoustic sounding of an inhomogeneous medium in a cylindrical region is proposed. The data of the problem is the complex amplitude of the wave field, measured outside the region of acoustic inhomogeneities in a cylindrical layer. Using the Fourier transform and Fourier series, the inverse problem is reduced to solving a set of one-dimensional Fredholm integral equations of the first kind, to the subsequent calculation of the complex amplitude of the wave field in the region of inhomogeneity, and then to finding the required sound velocity field in this region. The algorithm allows solving the inverse problem on a personal computer of average performance for sufficiently fine three-dimensional grids in tens of seconds. A numerical study of the accuracy of the proposed algorithm for solving model inverse problems at various frequencies is carried out, and the issues of stability of the algorithm with respect to data perturbations are investigated.