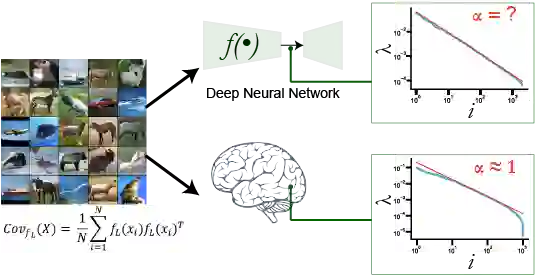
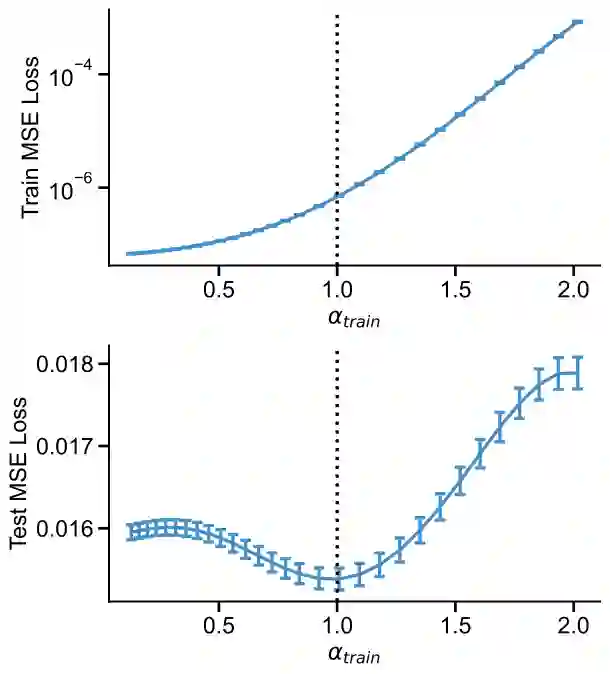
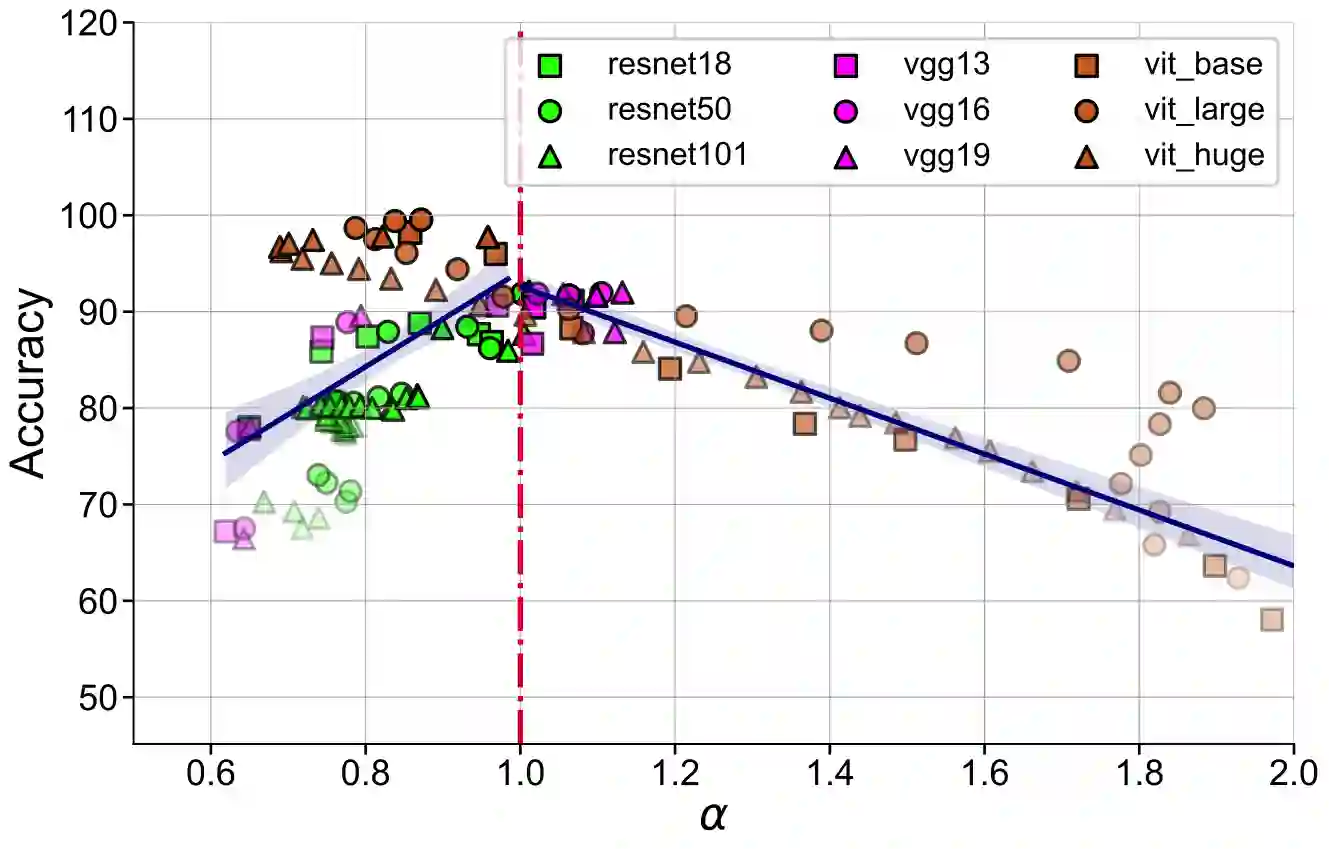
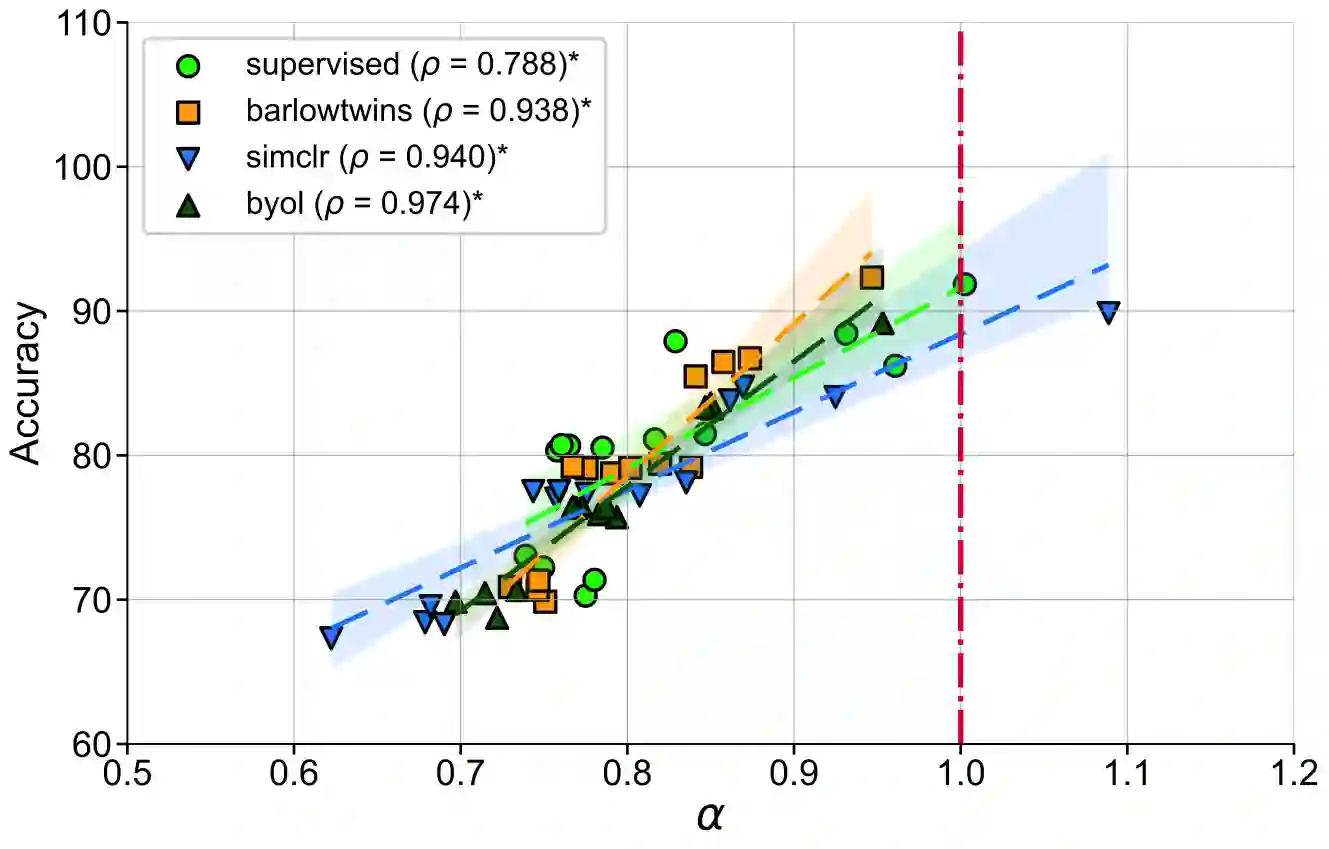
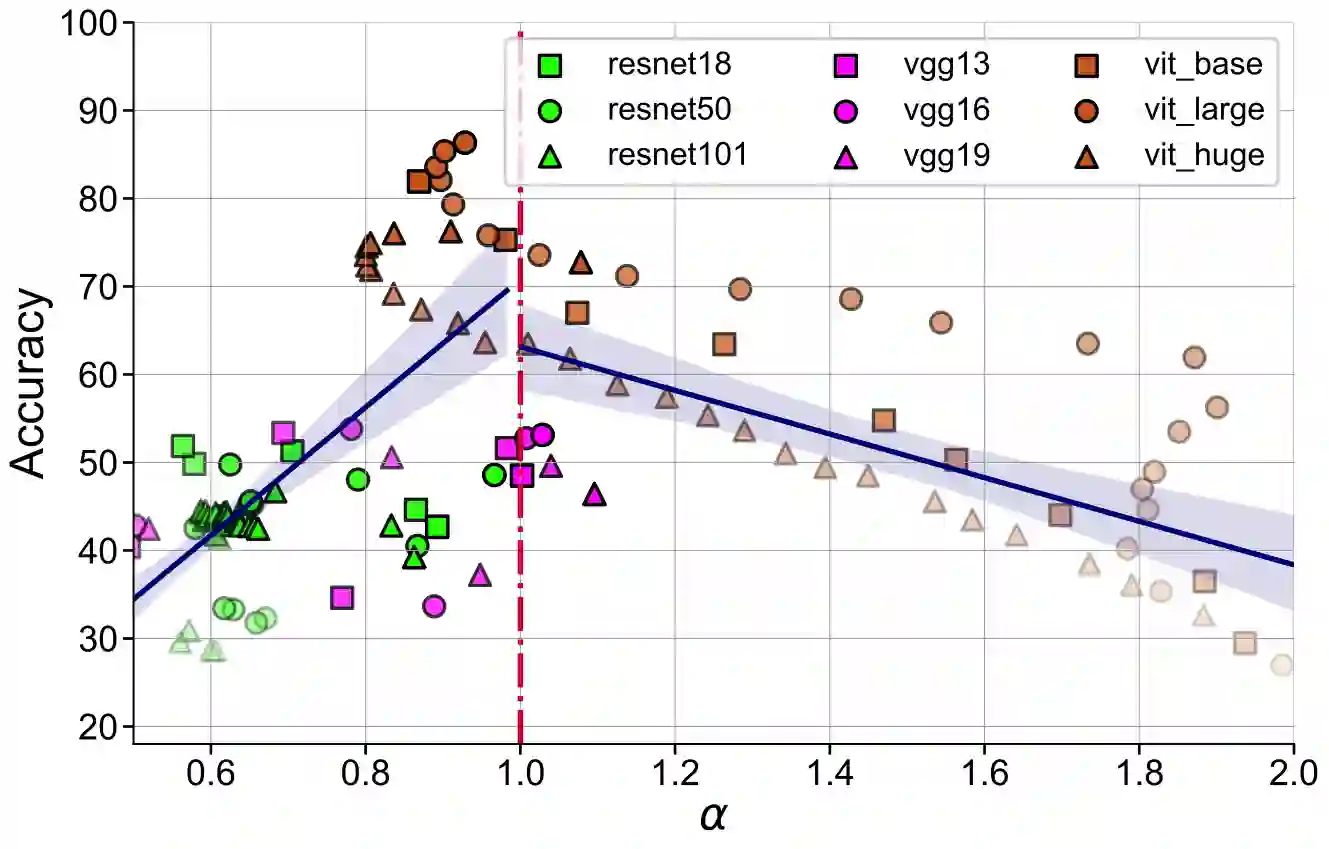
Representation learning that leverages large-scale labelled datasets, is central to recent progress in machine learning. Access to task relevant labels at scale is often scarce or expensive, motivating the need to learn from unlabelled datasets with self-supervised learning (SSL). Such large unlabelled datasets (with data augmentations) often provide a good coverage of the underlying input distribution. However evaluating the representations learned by SSL algorithms still requires task-specific labelled samples in the training pipeline. Additionally, the generalization of task-specific encoding is often sensitive to potential distribution shift. Inspired by recent advances in theoretical machine learning and vision neuroscience, we observe that the eigenspectrum of the empirical feature covariance matrix often follows a power law. For visual representations, we estimate the coefficient of the power law, $\alpha$, across three key attributes which influence representation learning: learning objective (supervised, SimCLR, Barlow Twins and BYOL), network architecture (VGG, ResNet and Vision Transformer), and tasks (object and scene recognition). We observe that under mild conditions, proximity of $\alpha$ to 1, is strongly correlated to the downstream generalization performance. Furthermore, $\alpha \approx 1$ is a strong indicator of robustness to label noise during fine-tuning. Notably, $\alpha$ is computable from the representations without knowledge of any labels, thereby offering a framework to evaluate the quality of representations in unlabelled datasets.
翻译:代表制学习能够利用大规模贴标签数据集,这是最近机器学习进展的核心。 获取规模上的任务相关标签往往稀缺或昂贵,促使人们需要通过自我监督学习(SSL)从未贴标签的数据集中学习。 如此庞大的未贴标签的数据集(配有数据扩增)往往能很好地覆盖基本输入分布。 然而,评价SSL算法所学的表述仍然需要培训管道中特定任务标签样本。 此外,任务特定编码的普及往往敏感于潜在的分配变化。在理论机器学习和视觉神经科学的最新进展的启发下,我们观察到经验性特征共变异矩阵的eigenspecrence常常遵循权力法。 对于视觉表达,我们估计权力法的系数为$alpha,这三大关键属性影响着代表学习:学习目标(超高、SimCLRR、Barlow Twins和BYOL)、网络结构(VGG、ResNet和VVV变异化器)以及任务(定位和场面识别)。我们观察到,在不温的条件下, 美元的标签结构中,美元比值值值比值比值更强的正标值比值比值比值比值比值为1期间,一个高的数据比值比值值值值值值值比值比值比值比值比值值值值值值值值值值值值值值值比值比值比值比值比值值值值值值值值值值值值值是一个高。