Markov Random Geometric Graph (MRGG): A Growth Model for Temporal Dynamic Networks

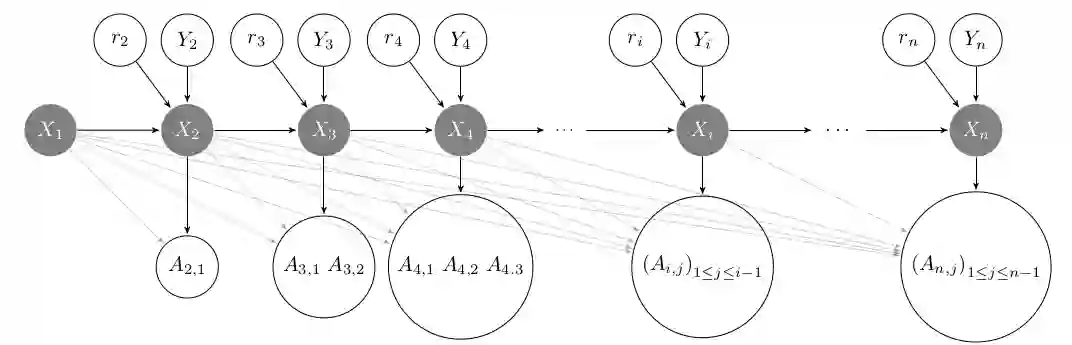
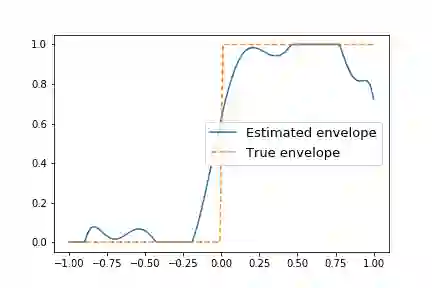
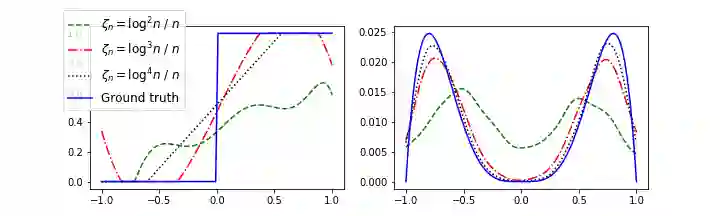
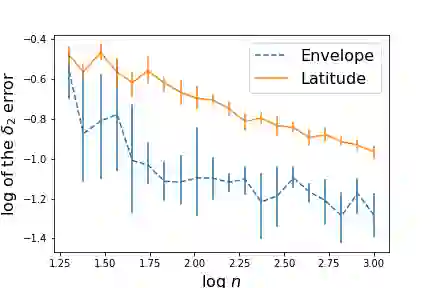
We introduce Markov Random Geometric Graphs (MRGGs), a growth model for temporal dynamic networks. It is based on a Markovian latent space dynamic: consecutive latent points are sampled on the Euclidean Sphere using an unknown Markov kernel; and two nodes are connected with a probability depending on a unknown function of their latent geodesic distance. More precisely, at each stamp-time k we add a latent point X k sampled by jumping from the previous one X k--1 in a direction chosen uniformly Y k and with a length r k drawn from an unknown distribution called the latitude function. The connection probabilities between each pair of nodes are equal to the envelope function of the distance between these two latent points. We provide theoretical guarantees for the non-parametric estimation of the latitude and the envelope functions. We propose an efficient algorithm that achieves those non-parametric estimation tasks based on an ad-hoc Hierarchical Agglomerative Clustering approach, and we deploy this analysis on a real data-set given by exchange of messages on a social network.