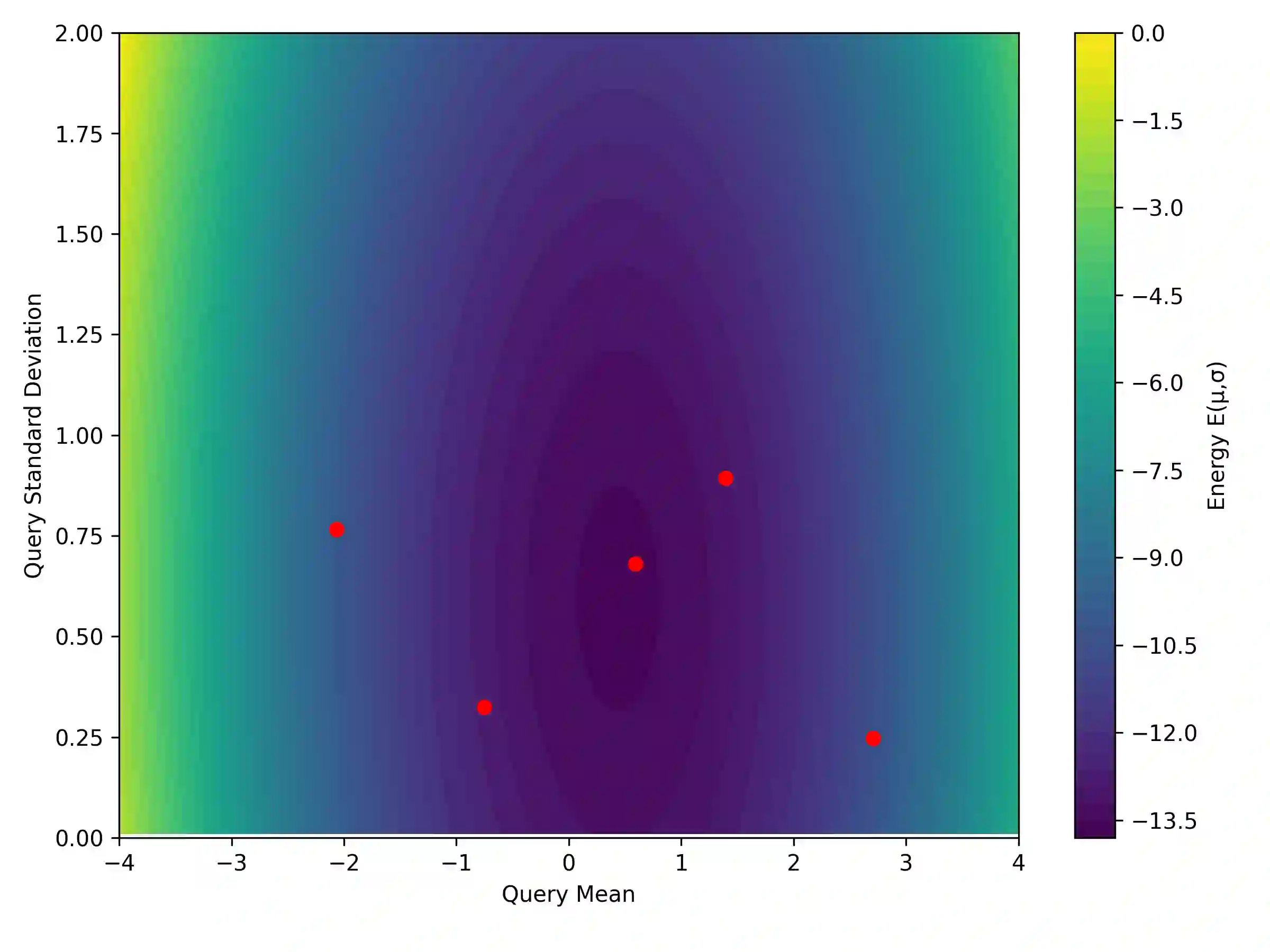
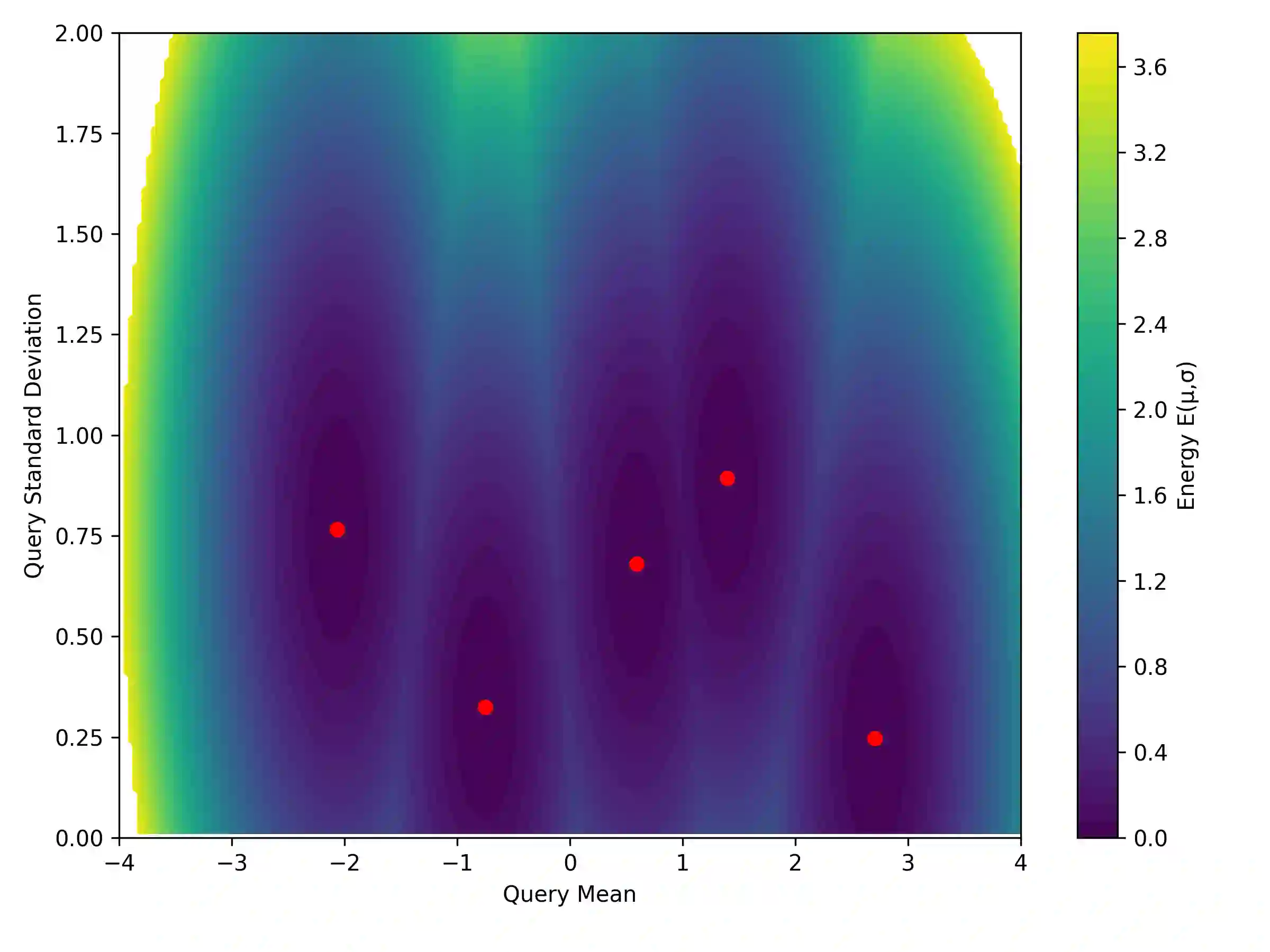
Dense associative memories (DAMs) store and retrieve patterns via energy-functional fixed points, but existing models are limited to vector representations. We extend DAMs to probability distributions equipped with the 2-Wasserstein distance, focusing mainly on the Bures-Wasserstein class of Gaussian densities. Our framework defines a log-sum-exp energy over stored distributions and a retrieval dynamics aggregating optimal transport maps in a Gibbs-weighted manner. Stationary points correspond to self-consistent Wasserstein barycenters, generalizing classical DAM fixed points. We prove exponential storage capacity, provide quantitative retrieval guarantees under Wasserstein perturbations, and validate the model on synthetic and real-world distributional tasks. This work elevates associative memory from vectors to full distributions, bridging classical DAMs with modern generative modeling and enabling distributional storage and retrieval in memory-augmented learning.
翻译:稠密联想记忆(Dense associative memories, DAMs)通过能量泛函的固定点来存储和检索模式,但现有模型仅限于向量表示。我们将DAMs扩展至配备2-Wasserstein距离的概率分布,主要关注高斯密度中的Bures-Wasserstein类。我们的框架定义了存储分布上的对数-求和-指数能量,以及以吉布斯加权方式聚合最优传输映射的检索动力学。其平稳点对应于自洽的Wasserstein重心,推广了经典DAM固定点。我们证明了指数级的存储容量,提供了Wasserstein扰动下的定量检索保证,并在合成与真实世界的分布任务上验证了该模型。这项工作将联想记忆从向量提升至完整分布,连接了经典DAMs与现代生成建模,并实现了记忆增强学习中的分布存储与检索。