An Marching Cube Algorithm Based on Edge Growth

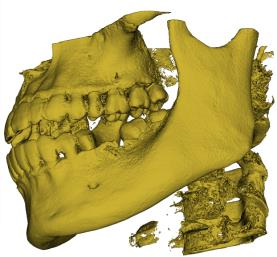
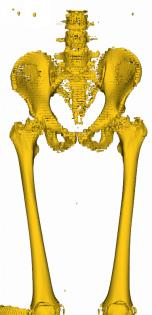
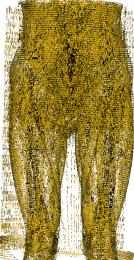
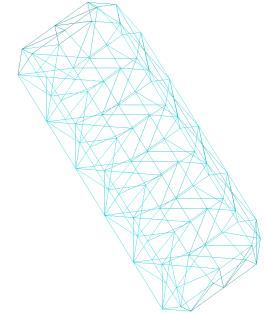
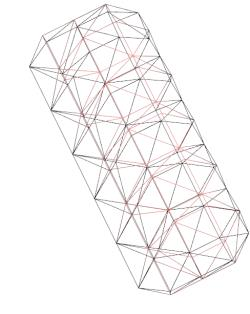
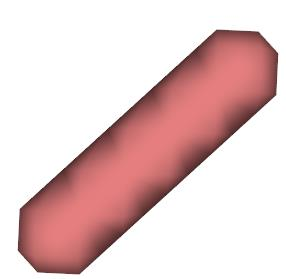
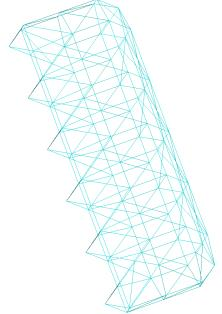
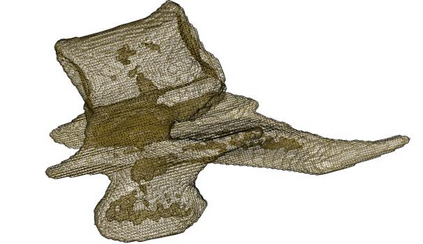
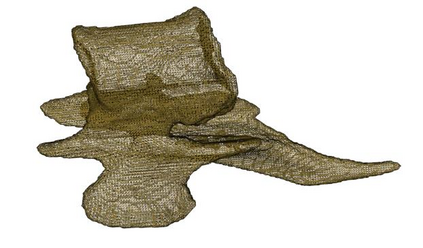
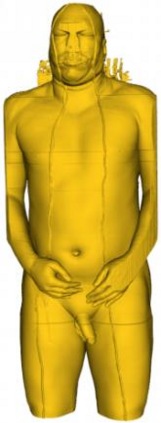
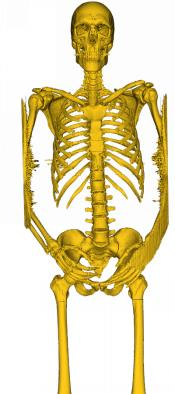
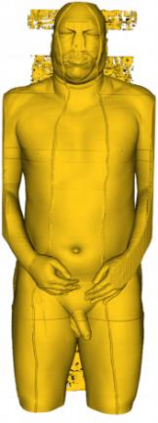
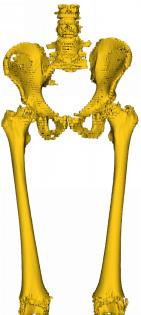
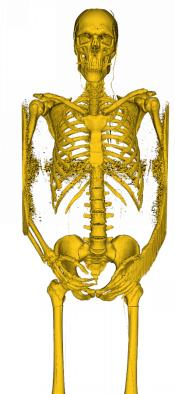
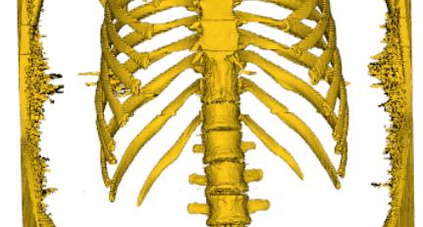
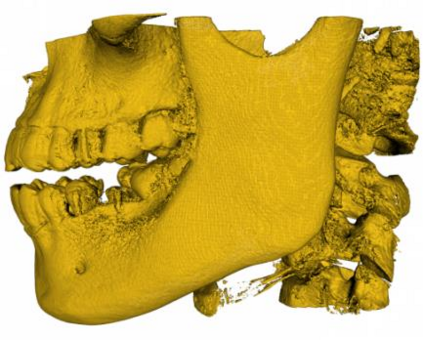
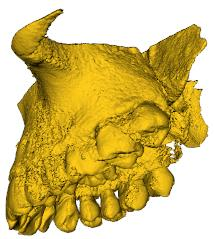
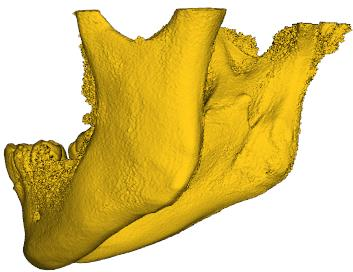
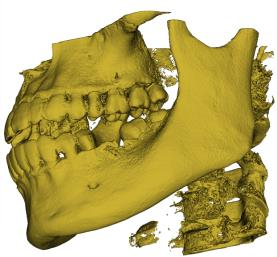
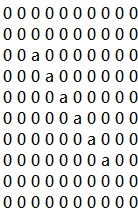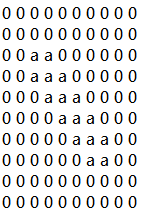Marching Cube algorithm is currently one of the most popular 3D reconstruction surface rendering algorithms.It forms cube voxels through the input image, and then uses 15 basic topological configurations to extract the isosurfaces in the voxels.Since it processes each cube voxel in a traversal manner, it does not consider the relationship between isosurfaces in adjacent cubes.Due to ambiguity, the final reconstructed model may have holes.We propose a Marching Cube algorithm based on edge growth. The algorithm first extracts seed triangles, then grows the seed triangles and reconstructs the entire 3D model.According to the position of the growth edge, we propose 17 topological configurations with isosurfaces.From the reconstruction results, the algorithm can reconstruct the 3D model well. When only the main contour of the 3D model needs to be organized, the algorithm performs well.In addition, when there are multiple scattered parts in the data, the algorithm can extract only the three-dimensional contours of the parts connected to the seed by setting the region selected by the seed.