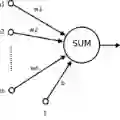
Artificial neural networks (ANNs) have very successfully been used in numerical simulations for a series of computational problems ranging from image classification/image recognition, speech recognition, time series analysis, game intelligence, and computational advertising to numerical approximations of partial differential equations (PDEs). Such numerical simulations suggest that ANNs have the capacity to very efficiently approximate high-dimensional functions and, especially, indicate that ANNs seem to admit the fundamental power to overcome the curse of dimensionality when approximating the high-dimensional functions appearing in the above named computational problems. There are a series of rigorous mathematical approximation results for ANNs in the scientific literature. Some of them prove convergence without convergence rates and some even rigorously establish convergence rates but there are only a few special cases where mathematical results can rigorously explain the empirical success of ANNs when approximating high-dimensional functions. The key contribution of this article is to disclose that ANNs can efficiently approximate high-dimensional functions in the case of numerical approximations of Black-Scholes PDEs. More precisely, this work reveals that the number of required parameters of an ANN to approximate the solution of the Black-Scholes PDE grows at most polynomially in both the reciprocal of the prescribed approximation accuracy $\varepsilon > 0$ and the PDE dimension $d \in \mathbb{N}$. We thereby prove, for the first time, that ANNs do indeed overcome the curse of dimensionality in the numerical approximation of Black-Scholes PDEs.
翻译:人工神经网络 (ANNS) 被非常成功地用于一系列计算问题的数字模拟中,从图像分类/图像识别、语音识别、时间序列分析、游戏智能和计算广告到部分差异方程式(PDEs)的数值近似值等一系列计算问题,从图像分类/图像识别、语音识别、时间序列分析、游戏智能和计算广告,到部分差异方程式(PDEs)的数值近似值。这种数字模拟表明,ANNS有能力非常高效地近似高维功能,特别是表明,ANNS在接近高维功能时似乎承认了克服维度诅咒的根本力量。在科学文献中,ANNS有一系列严格的数学近似结果。其中一些结果证明,没有达到趋近率,甚至严格地建立了趋近率,但只有少数特殊的例子,数学结果能够准确地解释ANNS在接近高维功能功能时成功的经验。这一文章的主要贡献是表明,在黑-S Pcholes的数值近似值中,可以有效地估计NNDS 最需要的精确度参数数量。