The Surprising Benefits of Hysteresis in Unlimited Sampling: Theory, Algorithms and Experiments

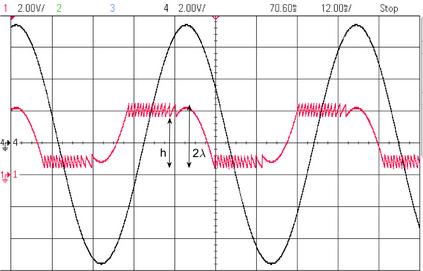
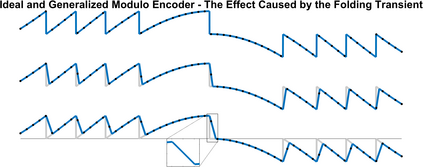
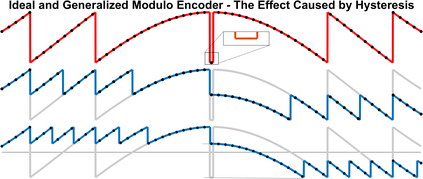
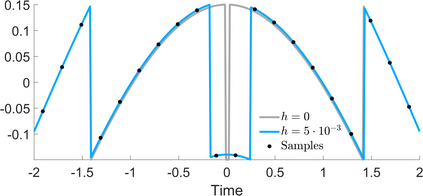
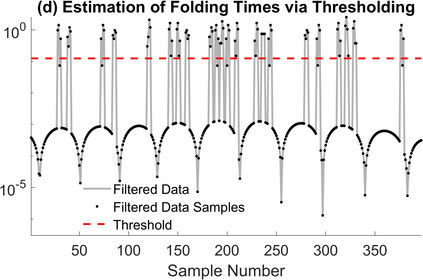
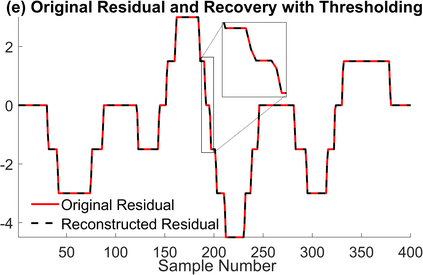
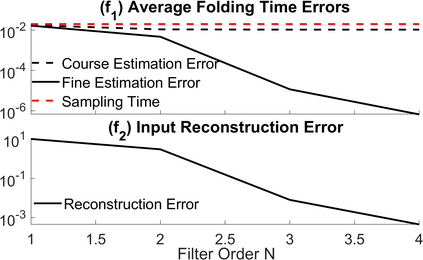
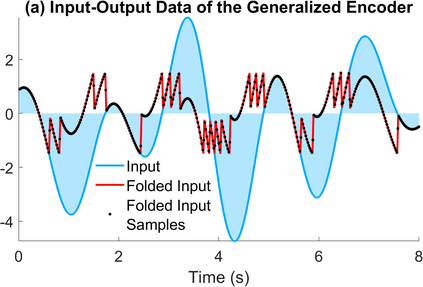
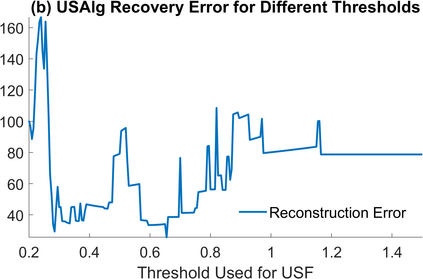
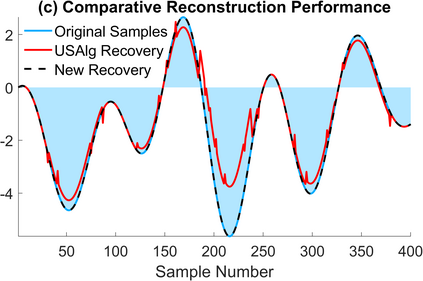
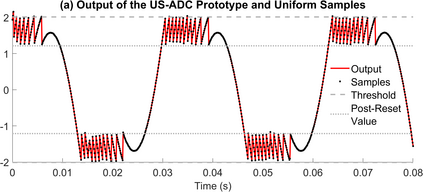
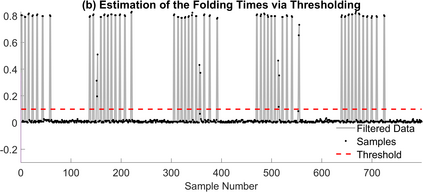
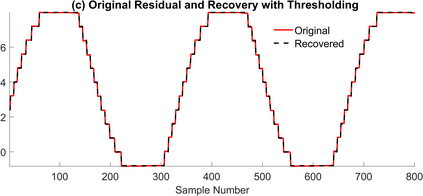
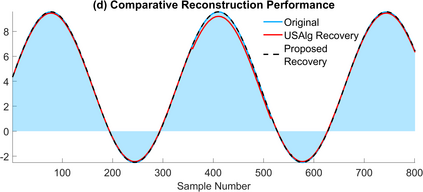
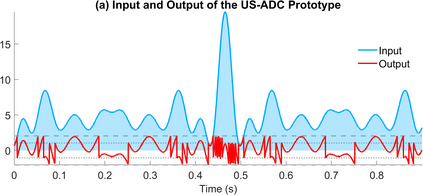
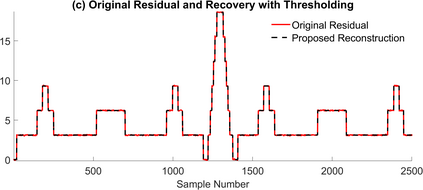
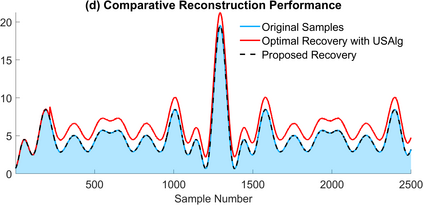
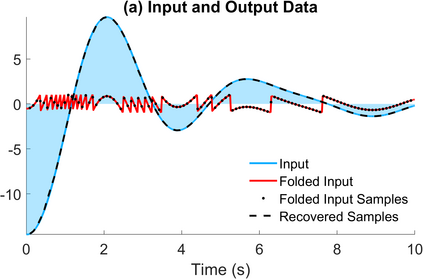
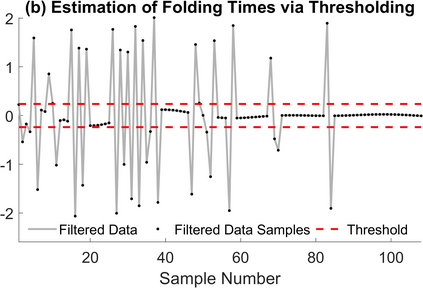
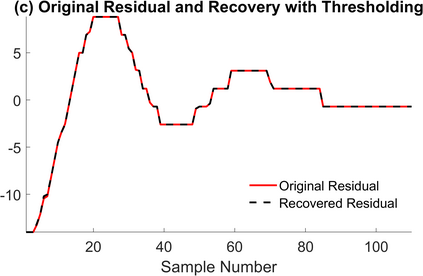
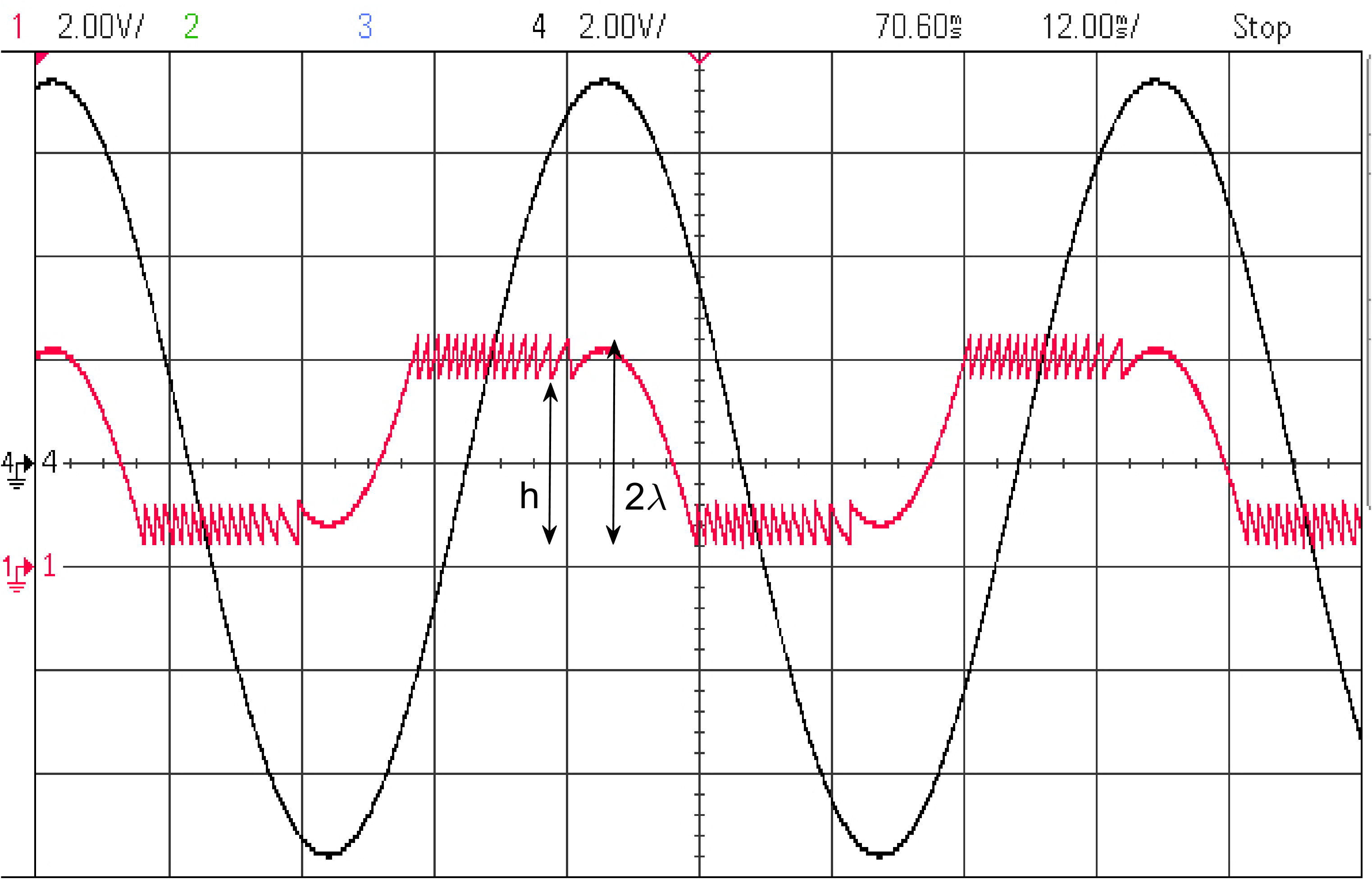
The Unlimited Sensing Framework (USF) was recently introduced to overcome the sensor saturation bottleneck in conventional digital acquisition systems. At its core, the USF allows for high-dynamic-range (HDR) signal reconstruction by converting a continuous-time signal into folded, low-dynamic-range (LDR), modulo samples. HDR reconstruction is then carried out by algorithmic unfolding of the folded samples. In hardware, however, implementing an ideal modulo folding requires careful calibration, analog design and high precision. At the interface of theory and practice, this paper explores a computational sampling strategy that relaxes strict hardware requirements by compensating them via a novel, mathematically guaranteed recovery method. Our starting point is a generalized model for USF. The generalization relies on two new parameters modeling hysteresis and folding transients} in addition to the modulo threshold. Hysteresis accounts for the mismatch between the reset threshold and the amplitude displacement at the folding time and we refer to a continuous transition period in the implementation of a reset as folding transient. Both these effects are motivated by our hardware experiments and also occur in previous, domain-specific applications. We show that the effect of hysteresis is beneficial for the USF and we leverage it to derive the first recovery guarantees in the context of our generalized USF model. Additionally, we show how the proposed recovery can be directly generalized for the case of lower sampling rates. Our theoretical work is corroborated by hardware experiments that are based on a hysteresis enabled, modulo ADC testbed comprising off-the-shelf electronic components. Thus, by capitalizing on a collaboration between hardware and algorithms, our paper enables an end-to-end pipeline for HDR sampling allowing more flexible hardware implementations.