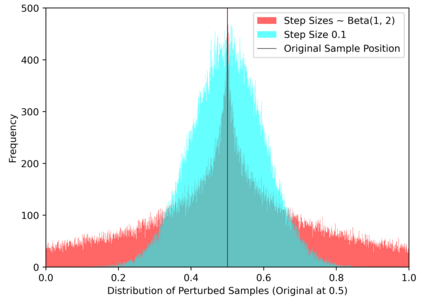
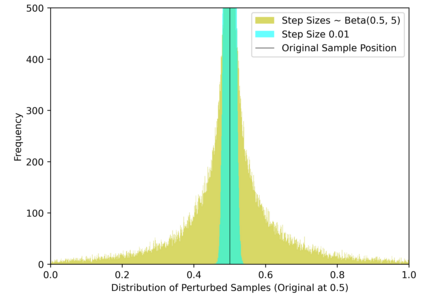
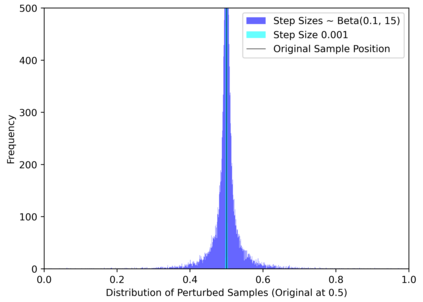
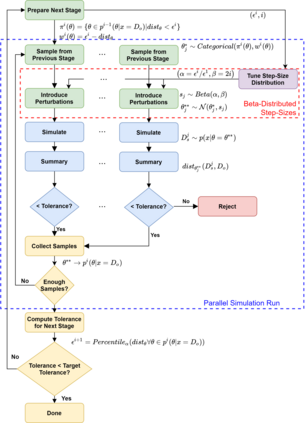
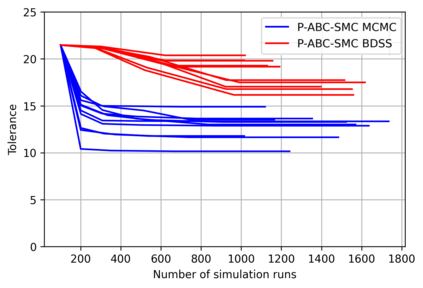
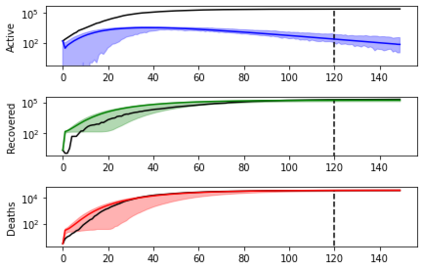
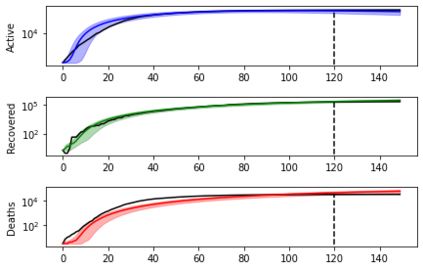
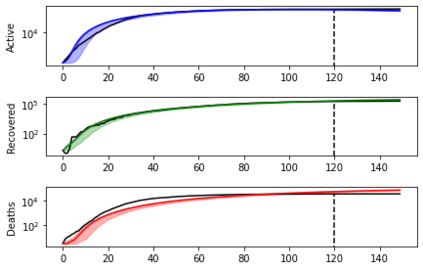
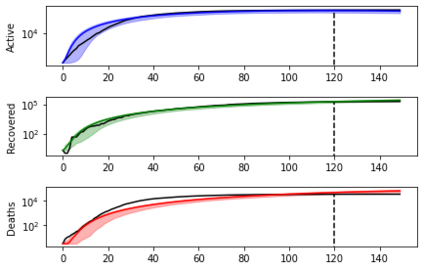
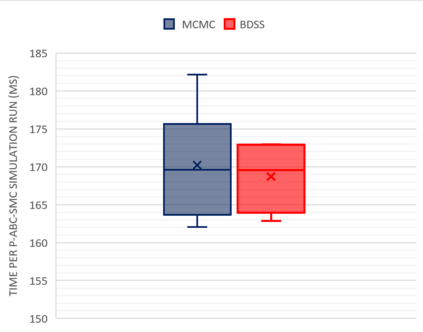
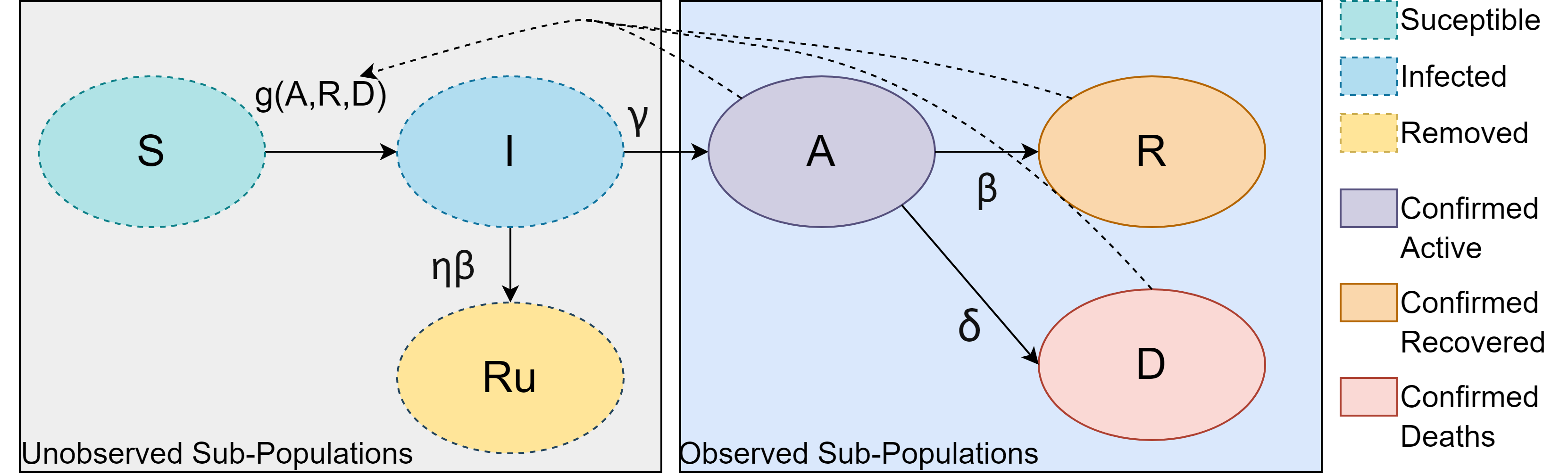
Simulation-based Inference (SBI) is a widely used set of algorithms to learn the parameters of complex scientific simulation models. While primarily run on CPUs in HPC clusters, these algorithms have been shown to scale in performance when developed to be run on massively parallel architectures such as GPUs. While parallelizing existing SBI algorithms provides us with performance gains, this might not be the most efficient way to utilize the achieved parallelism. This work proposes a new algorithm, that builds on an existing SBI method - Approximate Bayesian Computation with Sequential Monte Carlo(ABC-SMC). This new algorithm is designed to utilize the parallelism not only for performance gain, but also toward qualitative benefits in the learnt parameters. The key idea is to replace the notion of a single 'step-size' hyperparameter, which governs how the state space of parameters is explored during learning, with step-sizes sampled from a tuned Beta distribution. This allows this new ABC-SMC algorithm to more efficiently explore the state-space of the parameters being learnt. We test the effectiveness of the proposed algorithm to learn parameters for an epidemiology model running on a Tesla T4 GPU. Compared to the parallelized state-of-the-art SBI algorithm, we get similar quality results in $\sim 100$x fewer simulations and observe ~80x lower run-to-run variance across 10 independent trials.
翻译:模拟模拟推算(SBI) 是一套广泛使用的算法, 用于学习复杂的科学模拟模型的参数。 虽然这些算法主要运行在HPC组群的CPU上, 但是这些算法在开发时显示在性能上在业绩上的规模, 开发时要运行在大规模平行的结构上, 如 GPUs 。 虽然平行现有的SBI算法为我们提供了绩效收益, 但这可能不是利用所实现的平行法的最有效方法。 这项工作提出了一个新的算法, 以现有的SBI方法为基础 — 接近 Bayesian Computation with Secerntial Monte Carlo( ABC- SMC ABC- SMC ) 。 这个新的算法旨在不仅利用平行法来提高绩效, 而且在所学参数的质量方面也有好处。 关键的想法是取代单个“ 级大小” 超参数的概念, 该概念在学习期间如何探索参数的状态空间, 由调控的BC- SMC 新的ABC- SMC 调算法可以更独立地探索正在学的参数的状态空间。 我们测试拟议的算法的有效性, 在测试中, 类似的TRATIPL 的模型上, AS- 的比R 。