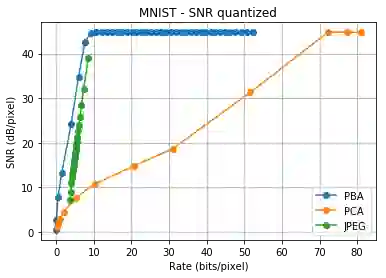
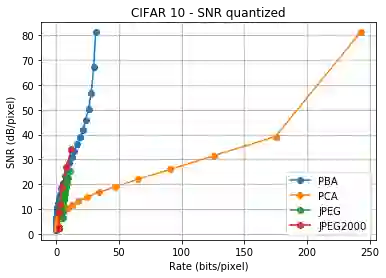
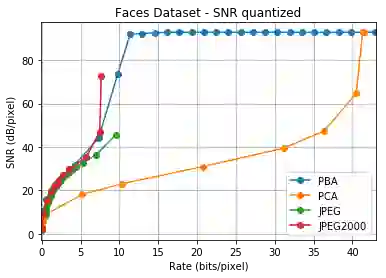
We consider a linear autoencoder in which the latent variables are quantized, or corrupted by noise, and the constraint is Schur-concave in the set of latent variances. Although finding the optimal encoder/decoder pair for this setup is a nonconvex optimization problem, we show that decomposing the source into its principal components is optimal. If the constraint is strictly Schur-concave and the empirical covariance matrix has only simple eigenvalues, then any optimal encoder/decoder must decompose the source in this way. As one application, we consider a strictly Schur-concave constraint that estimates the number of bits needed to represent the latent variables under fixed-rate encoding, a setup that we call \emph{Principal Bit Analysis (PBA)}. This yields a practical, general-purpose, fixed-rate compressor that outperforms existing algorithms. As a second application, we show that a prototypical autoencoder-based variable-rate compressor is guaranteed to decompose the source into its principal components.
翻译:我们考虑的是一个线性自动编码器,其潜在变量在其中被噪声量化或腐蚀,而制约因素是潜伏差异组中的Schur-concave。虽然找到用于此设置的最佳编码器/代coder对配对是一个非convex优化问题,但我们发现,将源分解成其主要组成部分是最佳的。如果该限制是严格意义上的Schur-concave,而实验性共变矩阵只有简单的叶素值,那么任何最佳编码器/脱coder都必须以这种方式解析源。作为一个应用程序,我们考虑严格的舒尔-cocive限制,即估计在固定节率编码中代表潜在变量所需的比特数,这是我们称之为\emph{主要比特分析(PBA)}的设置。这可以产生一种实用的、通用的、固定速率的压缩压缩器,它超越了现有的算法。作为第二个应用程序,我们证明基于正式自动自动编码的可变制式压缩压缩器保证将源解析成其主要组成部分。