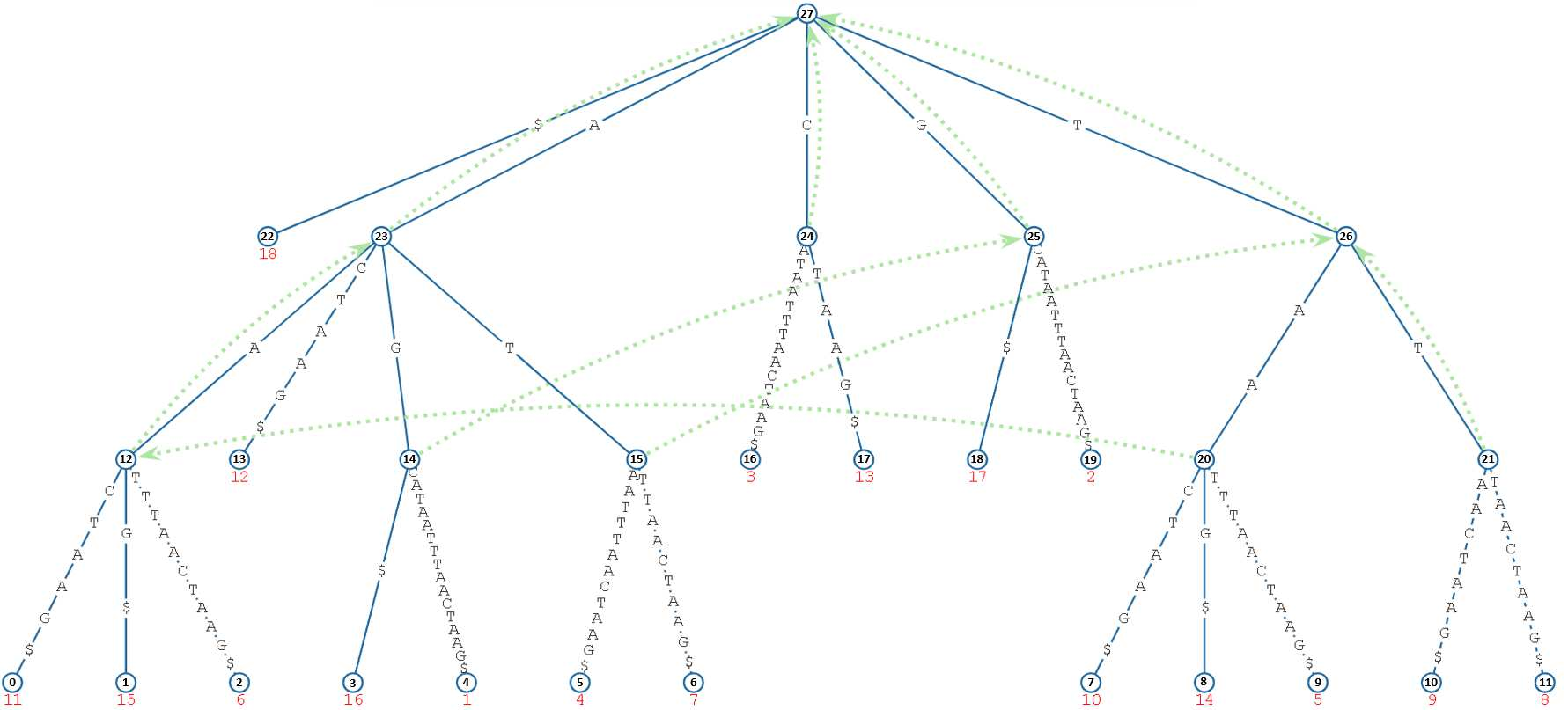
Pattern matching is a fundamental process in almost every scientific domain. The problem involves finding the positions of a given pattern (usually of short length) in a reference stream of data (usually of large length). The matching can be an exact or as an approximate (inexact). Exact matching is to search for the pattern without allowing for mismatches (or insertions and deletions) of one or more characters in the pattern), while approximate matching is the opposite. For exact matching, several data structures that can be built in linear time and space are used and in practice nowadays. For approximate matching, the solutions proposed to solve this matching are non-linear and currently impractical. In this paper, we designed and implemented a structure that can be built in linear time and space ($O(n)$) and solves the approximate matching problem in $O(m + \frac {log_2n {(log_\Sigma n)} ^{k+1}}{k!} + occ)$ search costs, where $m$ is the length of the pattern, $n$ is the length of the reference, and $k$ is the number of tolerated mismatches (and insertion and deletions).
翻译:在几乎每个科学领域,模式匹配都是一个基本的过程。 问题在于在数据参考流( 通常是长长的长度) 中找到特定模式的位置( 通常是短长的) 。 匹配可以是精确的, 也可以是近似( 不精确的) 。 精确的匹配是寻找模式, 不允许一个或一个以上字符在模式中出现不匹配( 插入和删除), 而近似匹配则相反 。 对于精确的匹配, 使用几个可以以线性时间和空间构建的数据结构, 并在目前实际操作中 。 对于近似匹配, 为解决这一匹配而提出的解决方案是非线性且目前不切实际的。 在本文中, 我们设计和实施了一个可以在线性时间和空间中构建的结构( (n) 美元), 并解决$O (m +\ frac {log_ 2n) { (( log_ sgma n}) } {k+1 ⁇ k+ occ) $ 搜索成本, 其中, $ 为模式的长度, $n 为参考长度, 和删除的长度, $k$ ( 和 $ 为可容忍性。) 。