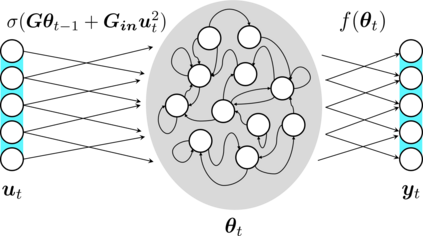
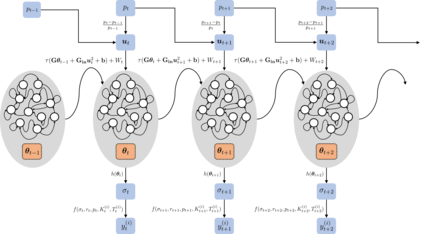
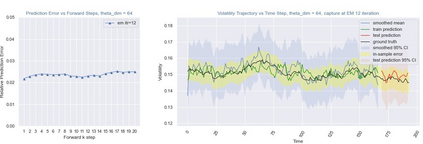
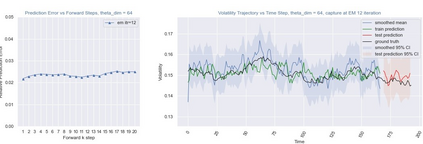
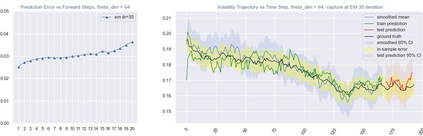
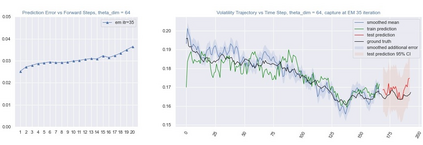
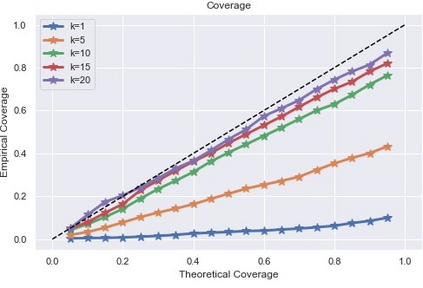
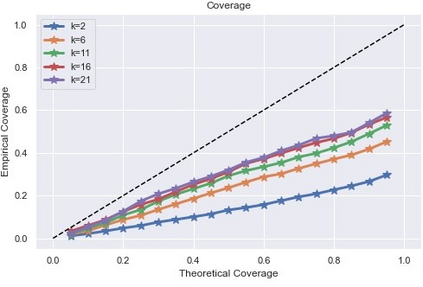
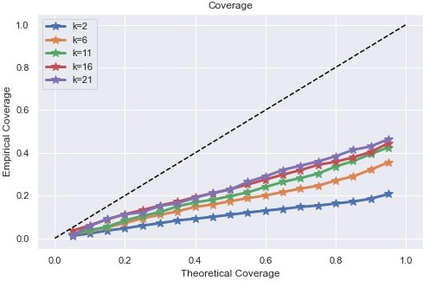
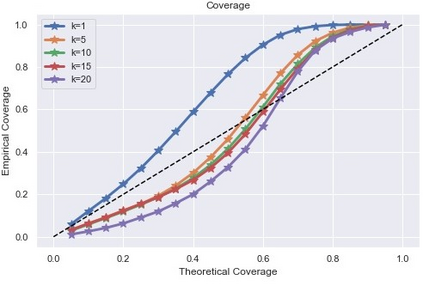
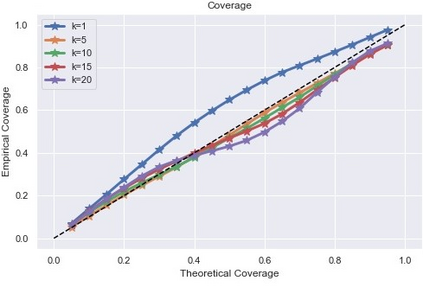
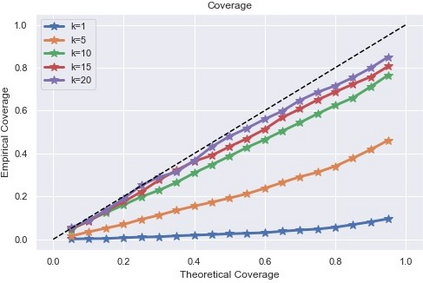
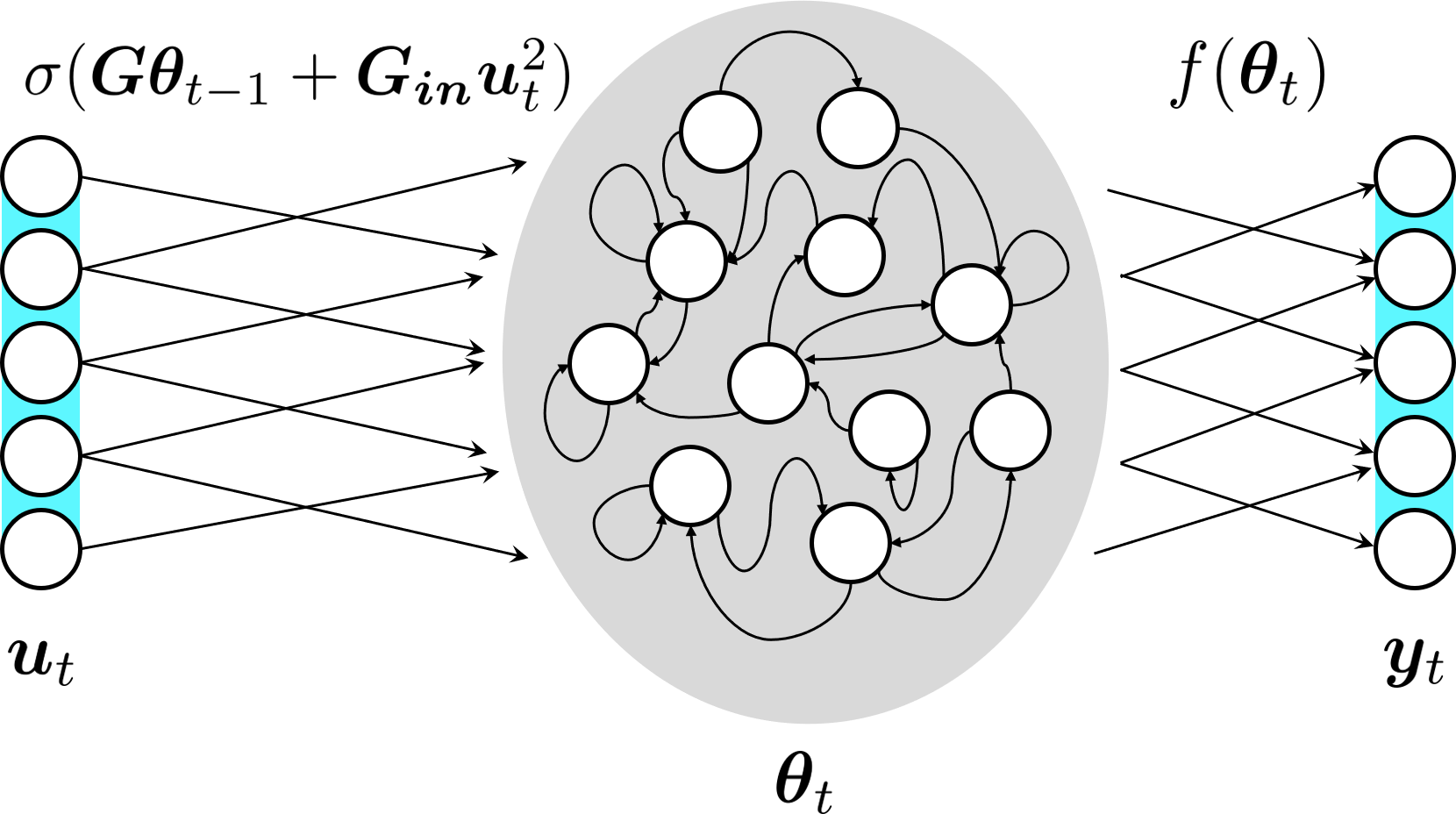
Inference and forecast problems of the nonlinear dynamical system have arisen in a variety of contexts. Reservoir computing and deep sequential models, on the one hand, have demonstrated efficient, robust, and superior performance in modeling simple and chaotic dynamical systems. However, their innate deterministic feature has partially detracted their robustness to noisy system, and their inability to offer uncertainty measurement has also been an insufficiency of the framework. On the other hand, the traditional state-space model framework is robust to noise. It also carries measured uncertainty, forming a just-right complement to the reservoir computing and deep sequential model framework. We propose the unscented reservoir smoother, a model that unifies both deep sequential and state-space models to achieve both frameworks' superiorities. Evaluated in the option pricing setting on top of noisy datasets, URS strikes highly competitive forecasting accuracy, especially those of longer-term, and uncertainty measurement. Further extensions and implications on URS are also discussed to generalize a full integration of both frameworks.
翻译:非线性动态系统的推论和预测问题在多种情况下都出现,一方面,储量计算和深层相继模型在简单和混乱动态系统的建模中显示了高效、稳健和优异的性能,然而,其内在的确定特征部分地削弱了其对噪音系统的稳健性,而且它们无法提供不确定性的测量也是框架的不足。另一方面,传统的州空间模型框架对噪音具有很强的威力,它也带有测量的不确定性,构成储油层计算和深层相继模型框架的正当性补充。我们提出了非中心储油层平滑模型,该模型将深层相继模型和州空间模型统一起来,以实现两个框架的优异性。在噪音数据集之上的选择定价中评估了紫外射线系统对高竞争性的预测准确性,特别是长期性和不确定性测量的准确性。还讨论了进一步扩展和对紫外光学模型的影响,以概括两个框架的全面整合。