Generalized Group Testing

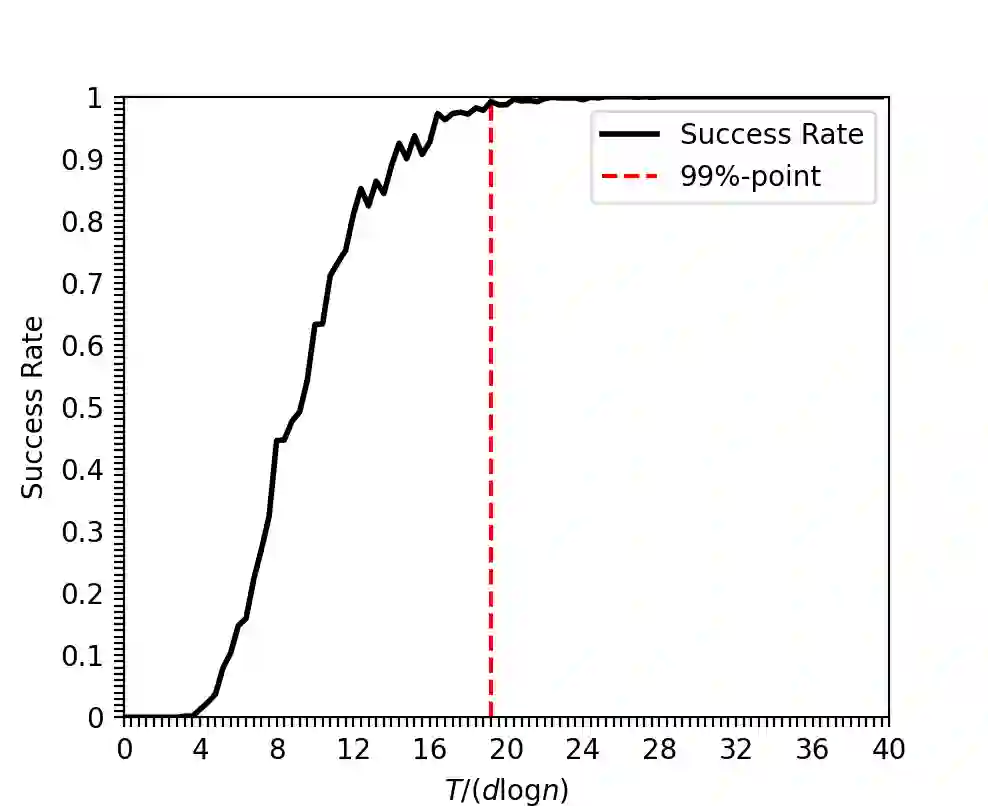
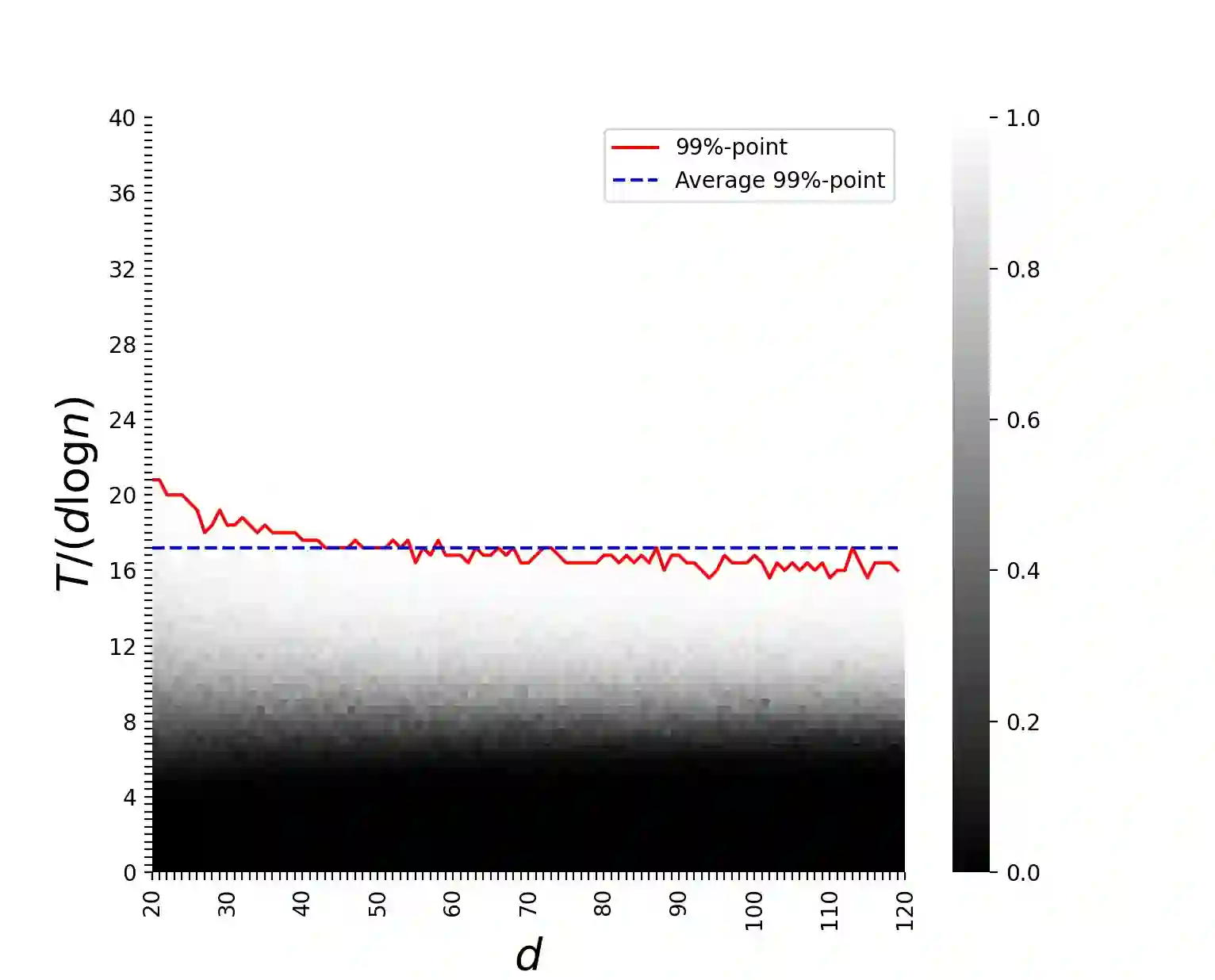
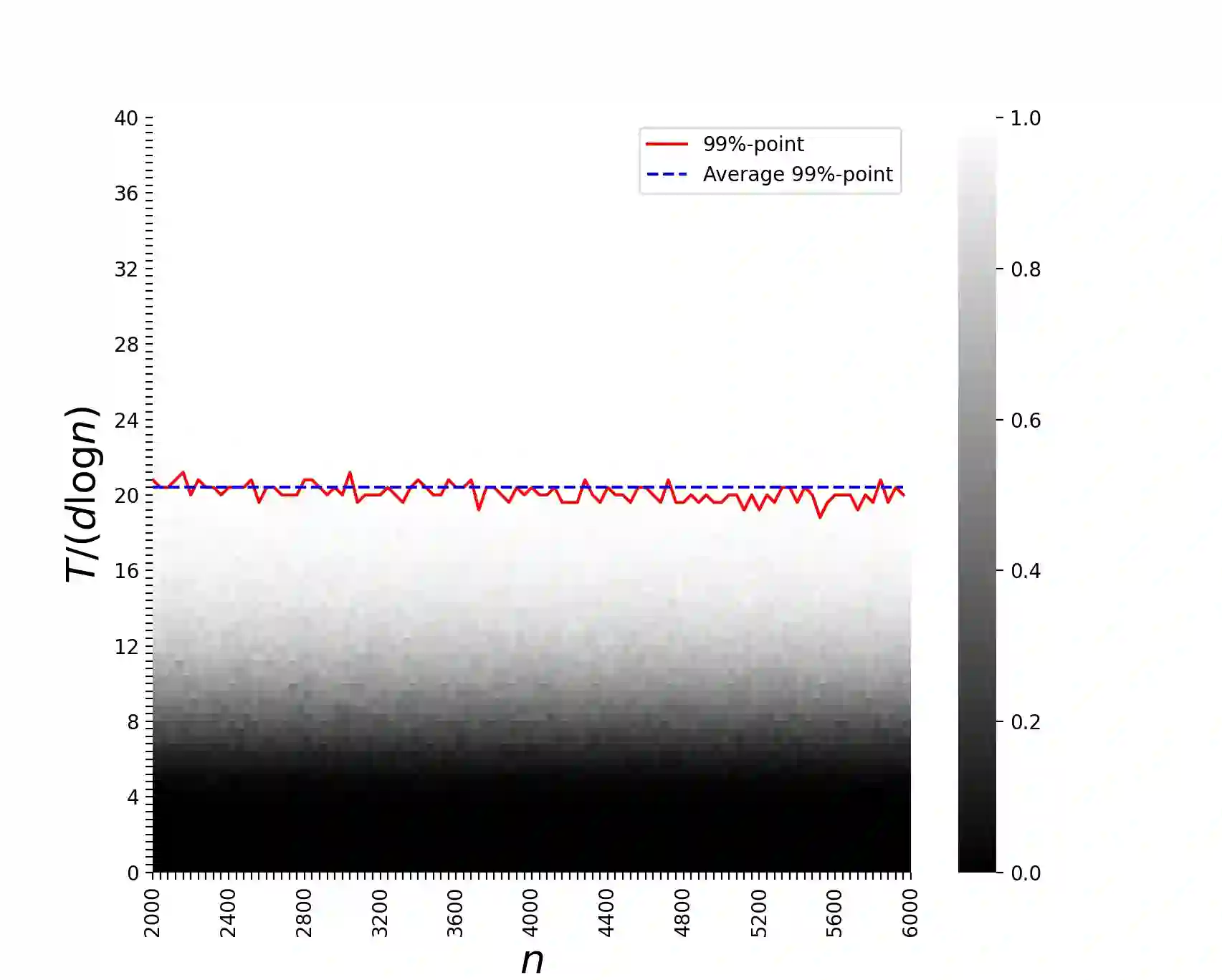
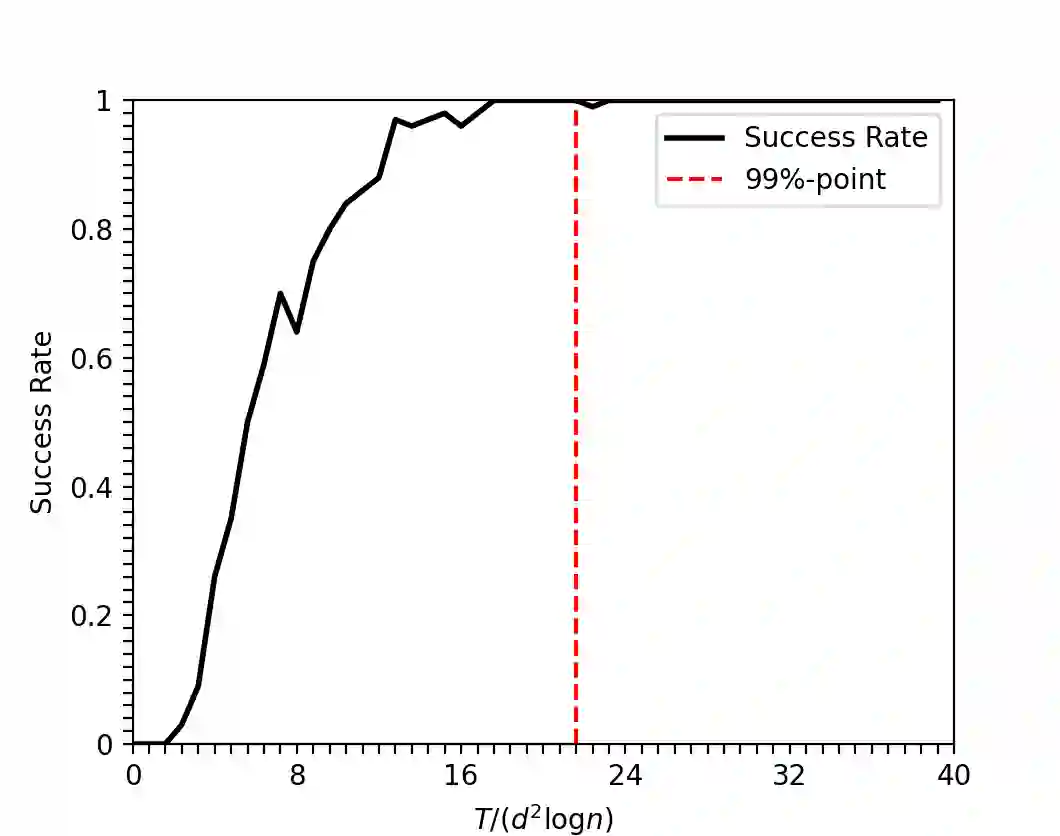
In the problem of classical group testing one aims to identify a small subset (of size $d$) diseased individuals/defective items in a large population (of size $n$). This process is based on a minimal number of suitably-designed group tests on subsets of items, where the test outcome is positive iff the given test contains at least one defective item. Motivated by physical considerations, we consider a generalized setting that includes as special cases multiple other group-testing-like models in the literature. In our setting, which subsumes as special cases a variety of noiseless and noisy group-testing models in the literature, the test outcome is positive with probability $f(x)$, where $x$ is the number of defectives tested in a pool, and $f(\cdot)$ is an arbitrary monotonically increasing (stochastic) test function. Our main contributions are as follows. 1. We present a non-adaptive scheme that with probability $1-\varepsilon$ identifies all defective items. Our scheme requires at most ${\cal O}( H(f) d\log\left(\frac{n}{\varepsilon}\right))$ tests, where $H(f)$ is a suitably defined "sensitivity parameter" of $f(\cdot)$, and is never larger than ${\cal O}\left(d^{1+o(1)}\right)$, but may be substantially smaller for many $f(\cdot)$. 2. We argue that any testing scheme (including adaptive schemes) needs at least $\Omega \left((1-\varepsilon)h(f) d\log\left(\frac n d\right)\right)$ tests to ensure reliable recovery. Here $h(f) \geq 1$ is a suitably defined "concentration parameter" of $f(\cdot)$. 3. We prove that $\frac{H(f)}{h(f)}\in\Theta(1)$ for a variety of sparse-recovery group-testing models in the literature, and $\frac {H(f)} {h(f)} \in {\cal O}\left(d^{1+o(1)}\right)$ for any other test function.