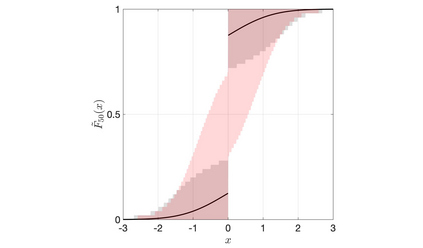
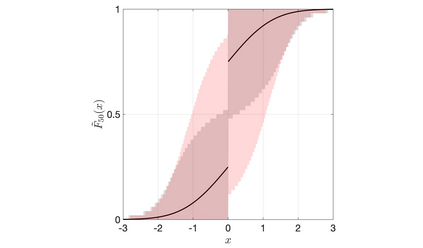
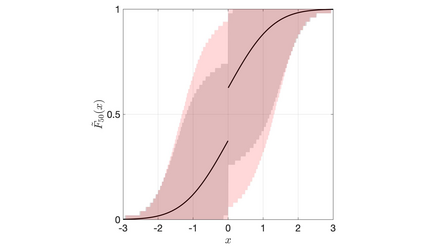
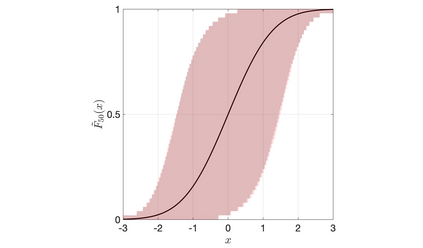
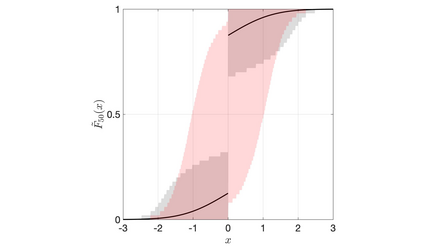
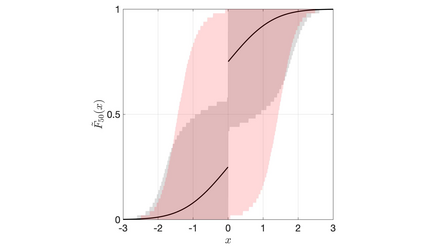
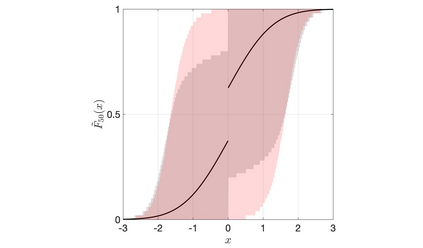
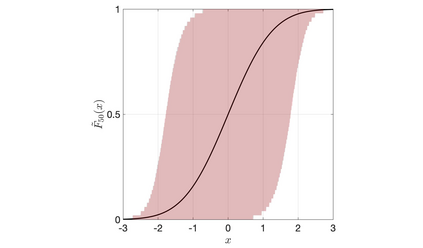
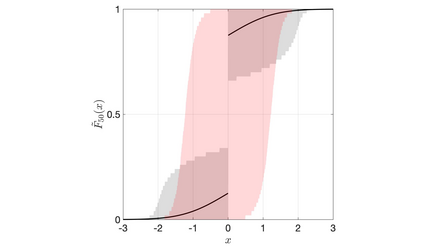
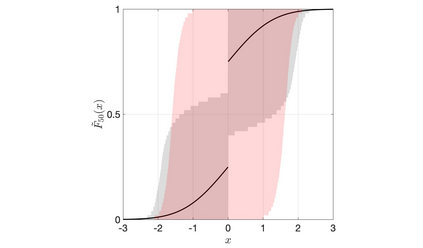
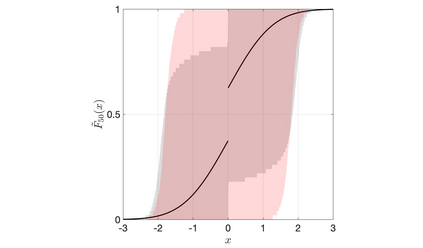
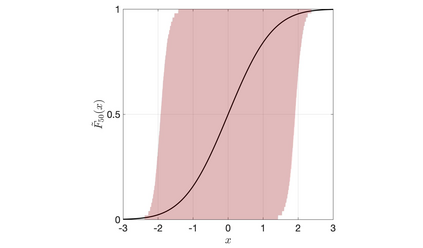
Discrete Bayesian nonparametric models whose expectation is a convex linear combination of a point mass at some point of the support and a diffuse probability distribution allow to incorporate strong prior information, while still being extremely flexible. Recent contributions in the statistical literature have successfully implemented such a modelling strategy in a variety of applications, including density estimation, nonparametric regression and model-based clustering. We provide a thorough study of a large class of nonparametric models we call inner spike and slab hNRMI models, which are obtained by considering homogeneous normalized random measures with independent increments (hNRMI) with base measure given by a convex linear combination of a point mass and a diffuse probability distribution. In this paper we investigate the distributional properties of these models and our results include: i) the exchangeable partition probability function they induce, ii) the distribution of the number of distinct values in an exchangeable sample, iii) the posterior predictive distribution, and iv) the distribution of the number of elements that coincide with the only point of the support with positive probability. Our findings are the main building block for an actual implementation of Bayesian inner spike and slab hNRMI models by means of a generalized P\'olya urn scheme.
翻译:Bayesian 分辨非参数模型,其预期值是在支持和分散概率分布的某个点质量上,一个点质量的分线线性线性组合,可以纳入强有力的先前信息,同时又仍然非常灵活。统计文献中最近的贡献在各种应用中成功地执行了这种模型战略,包括密度估计、非参数回归和基于模型的群集。我们提供了对大量非参数模型的透彻研究,我们称之为内尖峰和Slab hNRMI模型,这些模型是通过考虑同质的标准化标准随机计量,有独立递增(hNRMI),以点质量和扩散概率分布的点线性组合为基准计量,获得的。在本文件中,我们对这些模型的分布特性和我们的结果进行了调查,包括:i)这些模型的可互换分布概率功能,二)在可交换样品中的不同值的分布,三)后表预测分布,以及四)与唯一支持点一致的元素数量和积极概率。我们的调查结果是用Bayesrma 内核元钉和Slabsmal 方法实际实施Presmalmal main/rgetget 和Slagal 方法的主要构件。