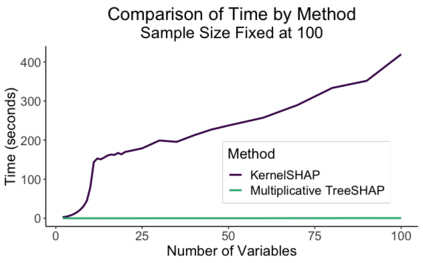
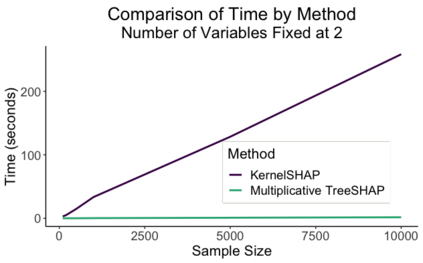
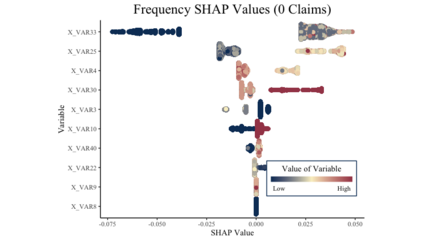
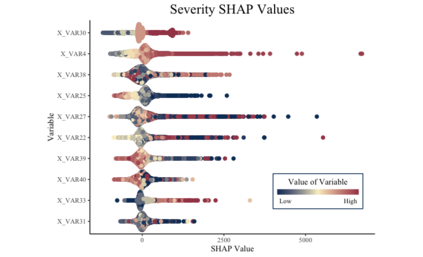
Two-part models are important to and used throughout insurance and actuarial science. Since insurance is required for registering a car, obtaining a mortgage, and participating in certain businesses, it is especially important that the models which price insurance policies are fair and non-discriminatory. Black box models can make it very difficult to know which covariates are influencing the results. SHAP values enable interpretation of various black box models, but little progress has been made in two-part models. In this paper, we propose mSHAP (or multiplicative SHAP), a method for computing SHAP values of two-part models using the SHAP values of the individual models. This method will allow for the predictions of two-part models to be explained at an individual observation level. After developing mSHAP, we perform an in-depth simulation study. Although the kernelSHAP algorithm is also capable of computing approximate SHAP values for a two-part model, a comparison with our method demonstrates that mSHAP is exponentially faster. Ultimately, we apply mSHAP to a two-part ratemaking model for personal auto property damage insurance coverage. Additionally, an R package (mshap) is available to easily implement the method in a wide variety of applications.
翻译:在保险和精算科学中,两部分模式很重要,并且在整个保险和精算科学中都使用。由于汽车登记、获得抵押贷款和参与某些企业都需要保险,因此特别重要的是,价格保险单的模型是公平和非歧视性的。黑盒模型可能很难知道哪些共变模型对结果产生影响。 SHAP 值有助于解释各种黑盒模型,但在两部分模型中进展甚微。在本文中,我们提议使用个人模型的SHAP值计算两部分模型的SHAP值的MSHAP值。这种方法将允许在个人观察层面上解释对两部分模型的预测。在开发 mSHAP之后,我们进行深入的模拟研究。虽然内核SHAP算法也能够计算出两部分模型的近似SHAP值,但与我们的方法相比,MSHAP是指数指数更快的。最终,我们将MSHAP应用于个人汽车损坏保险覆盖的两部分制率模型。此外,在开发MSHAP后,可以轻松地应用R包件。