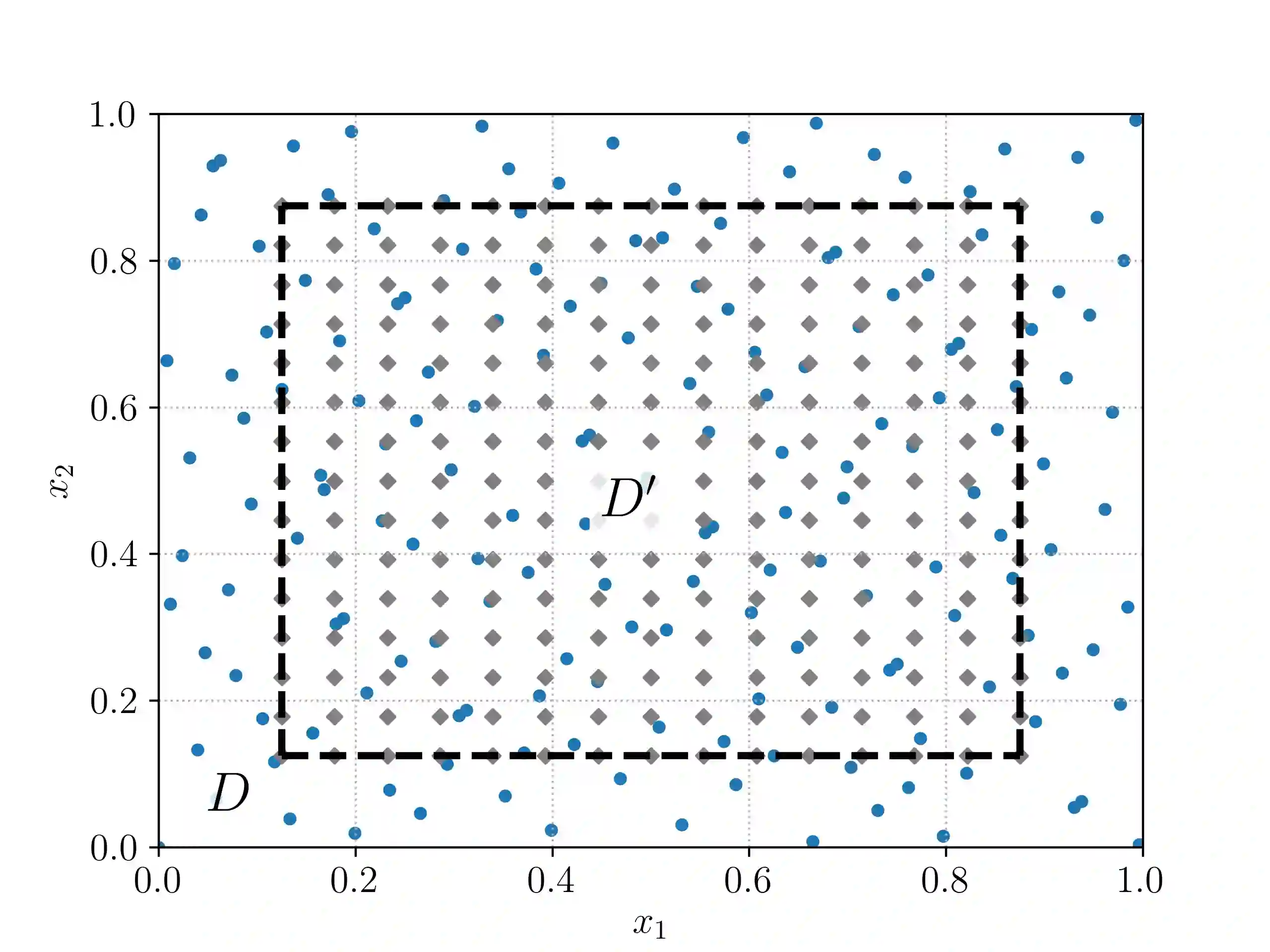
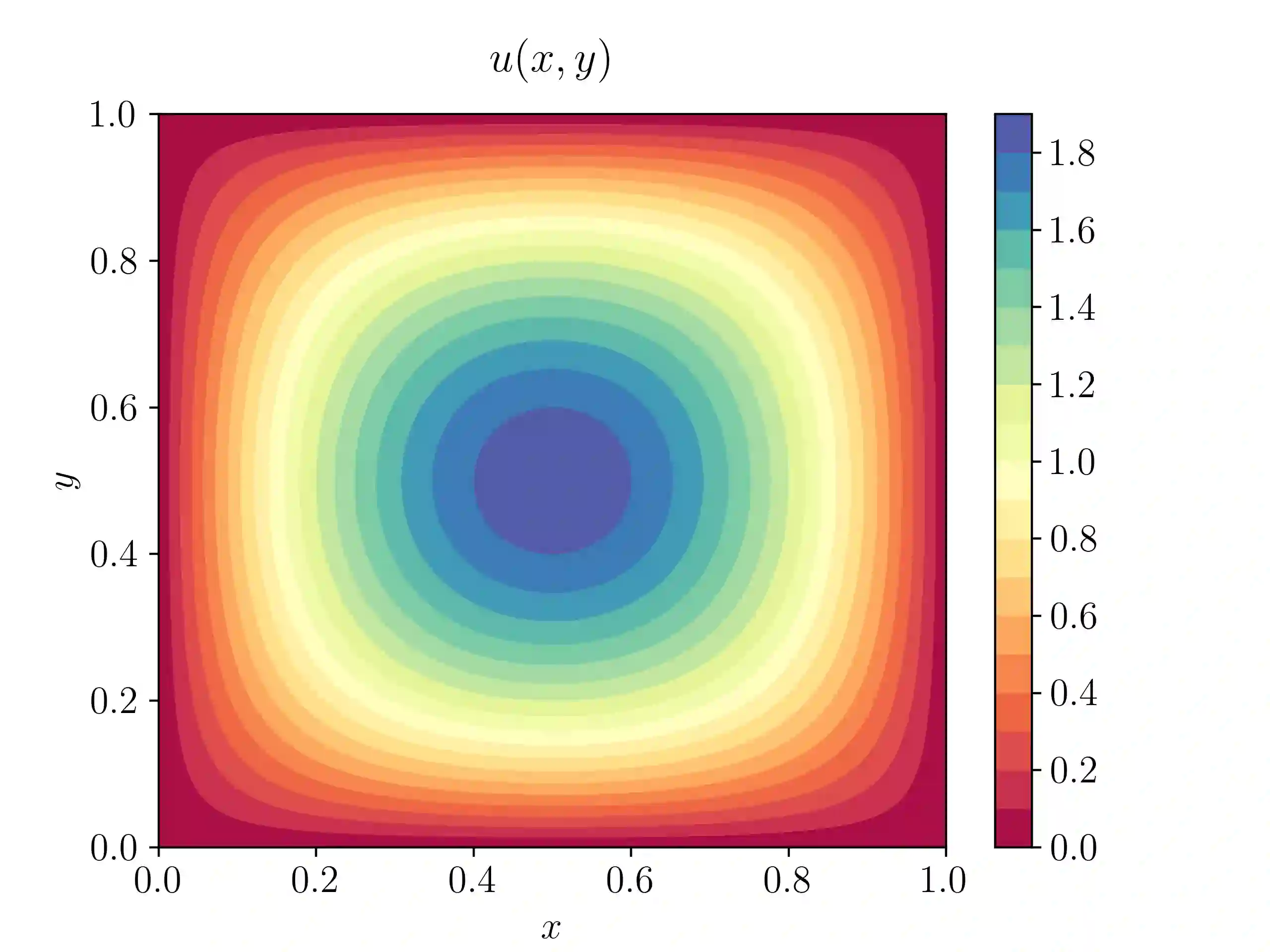
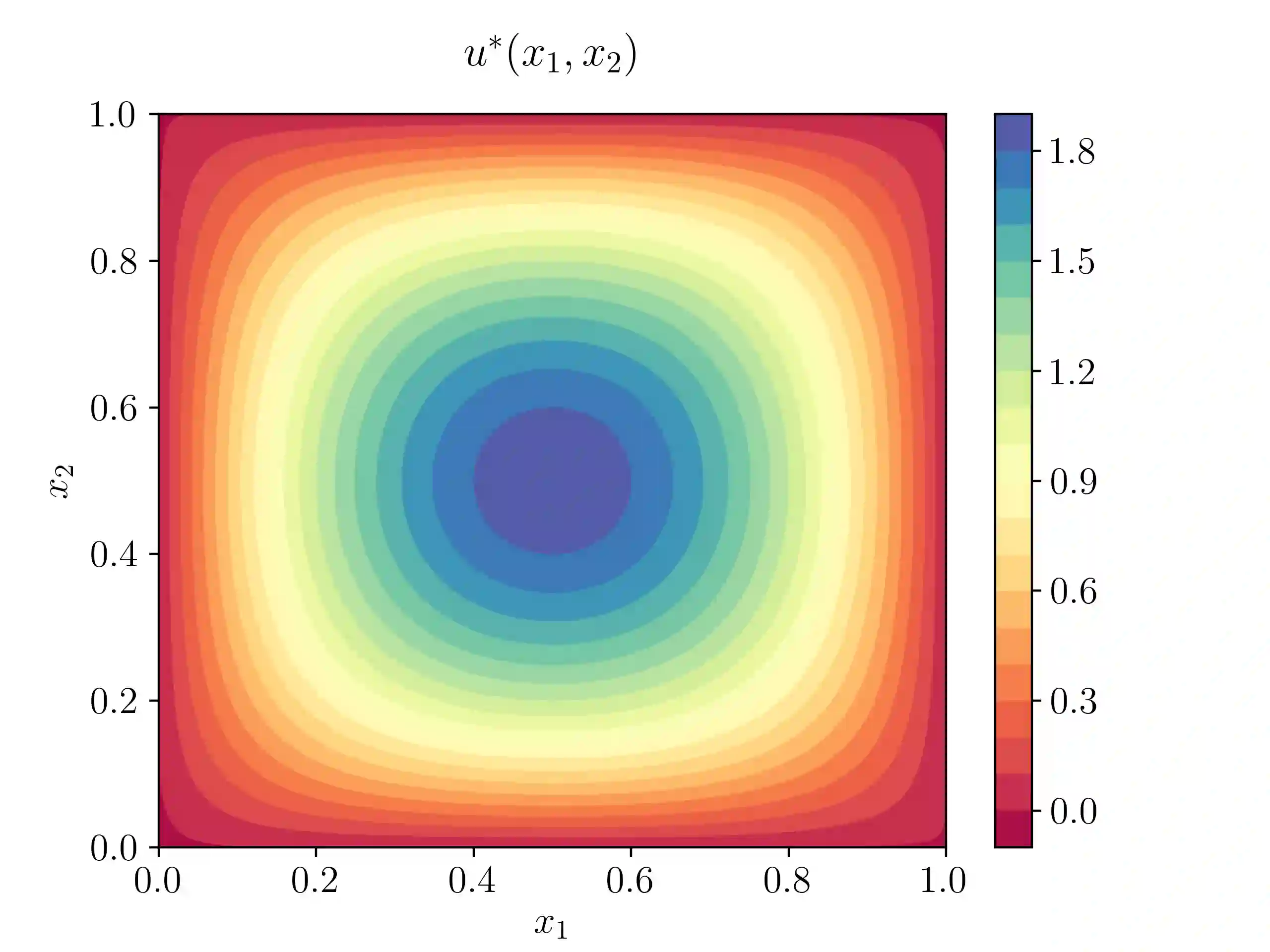
Physics informed neural networks (PINNs) have recently been very successfully applied for efficiently approximating inverse problems for PDEs. We focus on a particular class of inverse problems, the so-called data assimilation or unique continuation problems, and prove rigorous estimates on the generalization error of PINNs approximating them. An abstract framework is presented and conditional stability estimates for the underlying inverse problem are employed to derive the estimate on the PINN generalization error, providing rigorous justification for the use of PINNs in this context. The abstract framework is illustrated with examples of four prototypical linear PDEs. Numerical experiments, validating the proposed theory, are also presented.
翻译:物理学知情神经网络(PINNs)最近被非常成功地应用于高效近似于PDEs反面问题。我们集中关注一个特定类别的反面问题,即所谓的数据同化或独特的延续问题,并证明对PINNs接近PINNs的一般错误的严格估计。提出了抽象框架,并使用对潜在反向问题的有条件稳定估计来得出PINN一般化错误的估计,为在此情况下使用PINN提供了严格的理由。抽象框架以四种模拟线性PDEs的例子为例。还提出了验证拟议理论的数值实验。