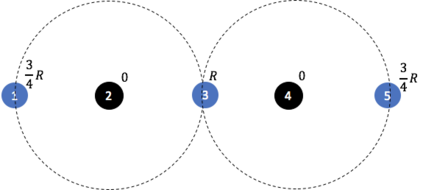
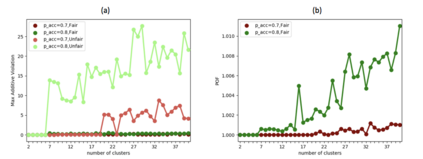
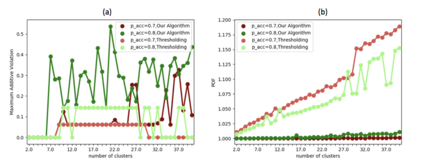
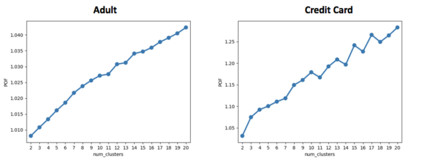
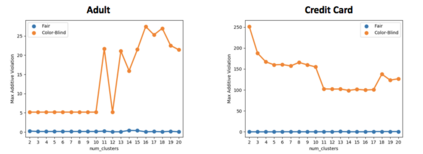
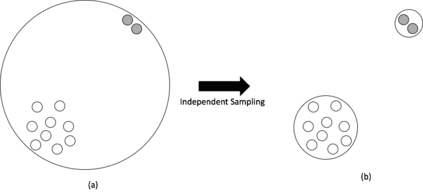
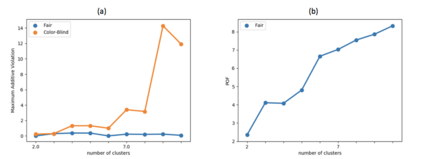
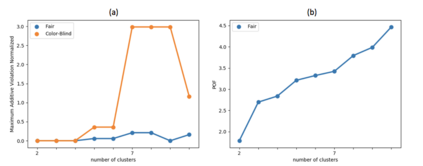
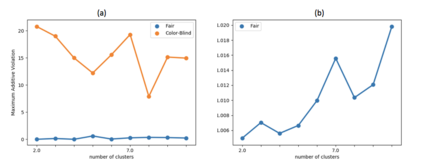
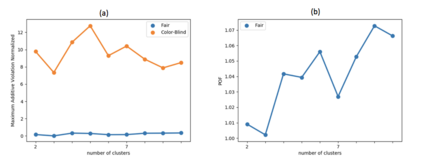
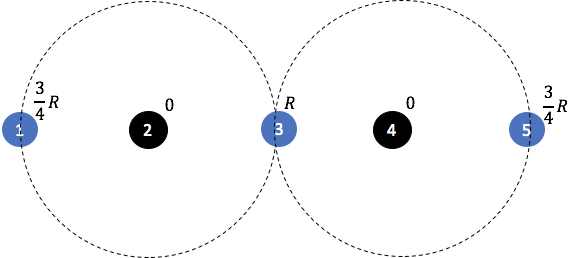
In clustering problems, a central decision-maker is given a complete metric graph over vertices and must provide a clustering of vertices that minimizes some objective function. In fair clustering problems, vertices are endowed with a color (e.g., membership in a group), and the features of a valid clustering might also include the representation of colors in that clustering. Prior work in fair clustering assumes complete knowledge of group membership. In this paper, we generalize prior work by assuming imperfect knowledge of group membership through probabilistic assignments. We present clustering algorithms in this more general setting with approximation ratio guarantees. We also address the problem of "metric membership", where different groups have a notion of order and distance. Experiments are conducted using our proposed algorithms as well as baselines to validate our approach and also surface nuanced concerns when group membership is not known deterministically.
翻译:在集群问题中,中央决策者在脊椎上获得完整的图解,必须提供能够最大限度地减少某种客观功能的脊椎群集。在公平的集群问题中,脊椎被赋予一种颜色(例如,加入一个集团),有效集群的特点也可能包括该集群中的颜色代表。先前的公平集群工作需要完全了解集团成员资格。在本文中,我们通过概率性任务假设对集团成员资格的不完全了解来概括先前的工作。我们在这个更一般性的设置中提出群集算法,提供近似比率保证。我们还处理“计量成员资格”问题,因为不同集团在其中具有秩序和距离的概念。我们利用拟议的算法和基线进行实验,以验证我们的做法,并在集团成员资格不为人们所熟知时进行表面微小的关注。