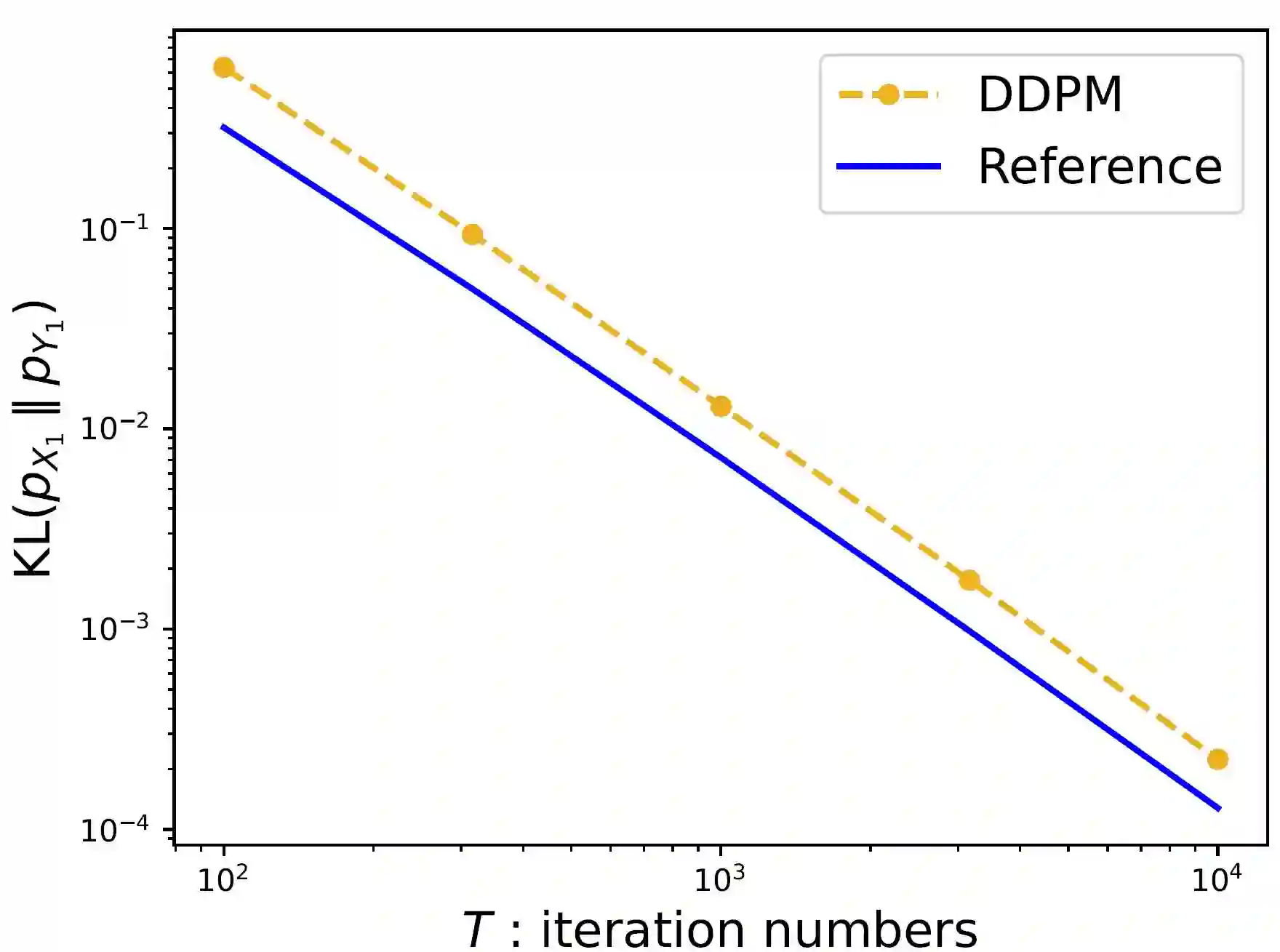
Score-based diffusion models have achieved remarkable empirical success in generating high-quality samples from target data distributions. Among them, the Denoising Diffusion Probabilistic Model (DDPM) is one of the most widely used samplers, generating samples via estimated score functions. Despite its empirical success, a tight theoretical understanding of DDPM -- especially its convergence properties -- remains limited. In this paper, we provide a refined convergence analysis of the DDPM sampler and establish near-optimal convergence rates under general distributional assumptions. Specifically, we introduce a relaxed smoothness condition parameterized by a constant $L$, which is small for many practical distributions (e.g., Gaussian mixture models). We prove that the DDPM sampler with accurate score estimates achieves a convergence rate of $$\widetilde{O}\left(\frac{d\min\{d,L^2\}}{T^2}\right)~\text{in Kullback-Leibler divergence},$$ where $d$ is the data dimension, $T$ is the number of iterations, and $\widetilde{O}$ hides polylogarithmic factors in $T$. This result substantially improves upon the best-known $d^2/T^2$ rate when $L < \sqrt{d}$. By establishing a matching lower bound, we show that our convergence analysis is tight for a wide array of target distributions. Moreover, it reveals that DDPM and DDIM share the same dependence on $d$, raising an interesting question of why DDIM often appears empirically faster.
翻译:基于分数的扩散模型在从目标数据分布中生成高质量样本方面取得了显著的实证成功。其中,去噪扩散概率模型(DDPM)是最广泛使用的采样器之一,通过估计的分数函数生成样本。尽管其实证表现优异,但对 DDPM 的严格理论理解——尤其是其收敛性质——仍然有限。本文对 DDPM 采样器进行了精细的收敛性分析,并在一般分布假设下建立了近乎最优的收敛速率。具体而言,我们引入了一个由常数 $L$ 参数化的松弛平滑性条件,该常数对于许多实际分布(例如高斯混合模型)较小。我们证明,在获得准确分数估计的情况下,DDPM 采样器在 Kullback-Leibler 散度下达到 $$\widetilde{O}\left(\frac{d\min\{d,L^2\}}{T^2}\right)$$ 的收敛速率,其中 $d$ 为数据维度,$T$ 为迭代次数,$\widetilde{O}$ 隐藏了 $T$ 的多对数因子。当 $L < \sqrt{d}$ 时,该结果显著优于已知的最佳 $d^2/T^2$ 速率。通过建立匹配的下界,我们证明了我们的收敛性分析对于广泛的目标分布是紧致的。此外,该分析揭示了 DDPM 与 DDIM 在 $d$ 上的依赖关系相同,这引发了一个有趣的问题:为何 DDIM 在实证中通常表现出更快的收敛速度。