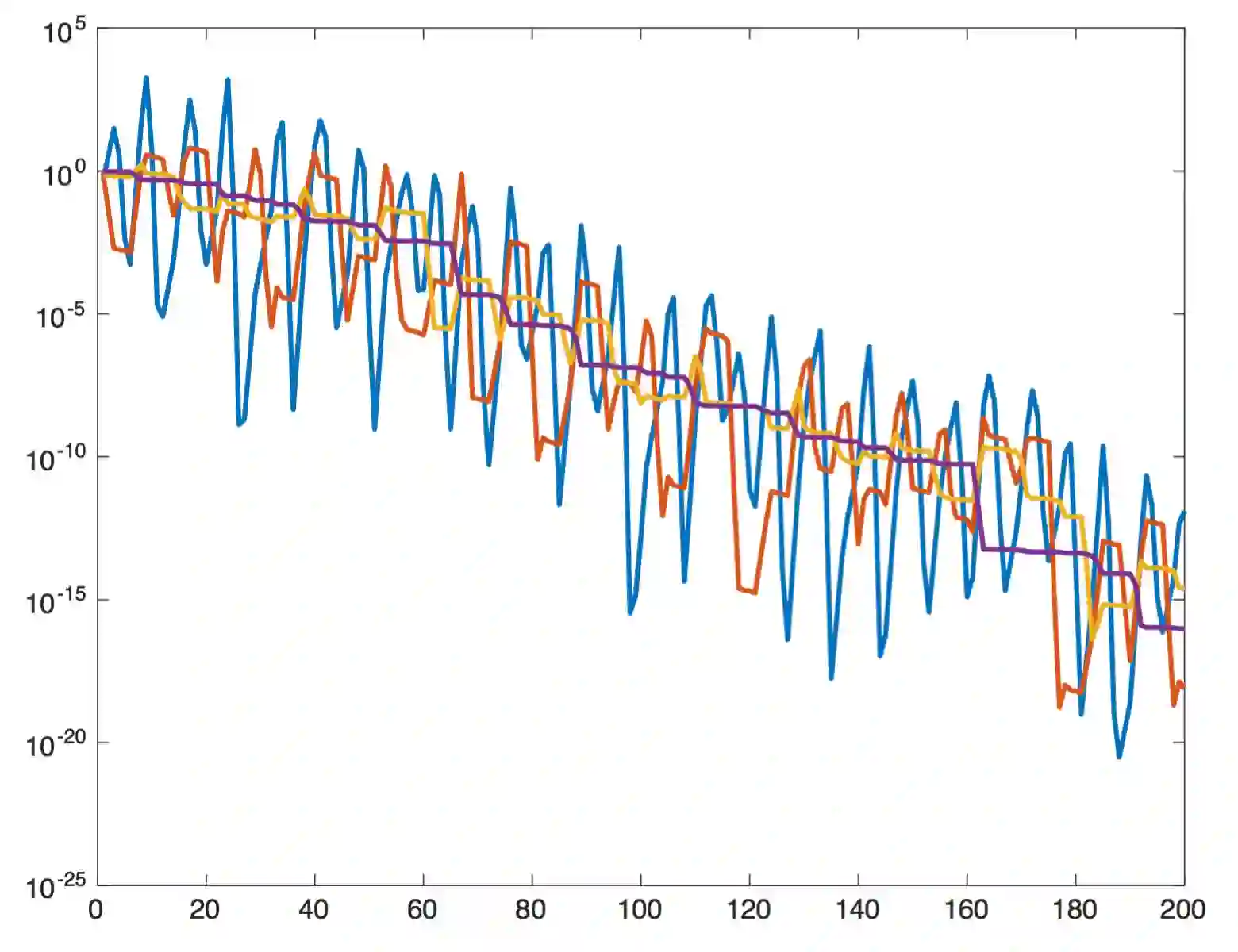
The Barzilai-Borwein (BB) method has demonstrated great empirical success in nonlinear optimization. However, the convergence speed of BB method is not well understood, as the known convergence rate of BB method for quadratic problems is much worse than the steepest descent (SD) method. Therefore, there is a large discrepancy between theory and practice. To shrink this gap, we prove that the BB method converges $R$-linearly at a rate of $1-1/\kappa$, where $\kappa$ is the condition number, for strongly convex quadratic problems. In addition, an example with the theoretical rate of convergence is constructed, indicating the tightness of our bound.
翻译:Barzilai-Borwein (BB) 方法在非线性优化方面表现出巨大的经验成功,但是,BB方法的趋同速度没有很好地理解,因为已知的BB方法对二次曲线问题的趋同速度比最陡峭的下降(SD)方法要差得多,因此,理论与实践之间有很大的差异。为了缩小这一差距,我们证明BB方法以1-1美元/kappa美元(美元是严重二次曲线问题的条件数)的汇率,即1-1美元/kappa美元(卡帕美元)为线性趋同速度。此外,还树立了一个理论趋同速度的例子,表明我们的界限很紧。