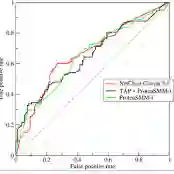
Performance measurement is an essential task once a statistical model is created. The Area Under the receiving operating characteristics Curve (AUC) is the most popular measure for evaluating the quality of a binary classifier. In this case, AUC is equal to the concordance probability, a frequently used measure to evaluate the discriminatory power of the model. Contrary to AUC, the concordance probability can also be extended to the situation with a continuous response variable. Due to the staggering size of data sets nowadays, determining this discriminatory measure requires a tremendous amount of costly computations and is hence immensely time consuming, certainly in case of a continuous response variable. Therefore, we propose two estimation methods that calculate the concordance probability in a fast and accurate way and that can be applied to both the discrete and continuous setting. Extensive simulation studies show the excellent performance and fast computing times of both estimators. Finally, experiments on two real-life data sets confirm the conclusions of the artificial simulations.
翻译:一旦创建了统计模型,绩效衡量就是一项基本任务。在接收的操作特性曲线(AUC)下的区域是评价二进制分类器质量的最受欢迎的衡量标准。在这种情况下,AUC等于一致性概率,这是用来评价模型歧视性力量的常用衡量标准。与AUC相反,一致性概率也可以以连续反应变量扩大到情况。由于当今数据集的惊人大小,确定这一歧视性计量需要大量昂贵的计算,因此耗时极大,当然是在连续反应变量的情况下。因此,我们建议两种估算方法,以快速和准确的方式计算一致性概率,并且可以适用于离散和连续的设置。广泛的模拟研究显示了两个估算器的出色性能和快速计算时间。最后,两个实时数据集的实验证实了人工模拟的结论。
相关内容
Source: Apple - iOS 8