Adaptive finite element approximations for elliptic problems using regularized forcing data

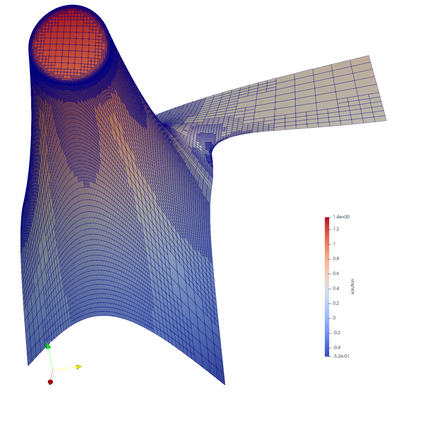
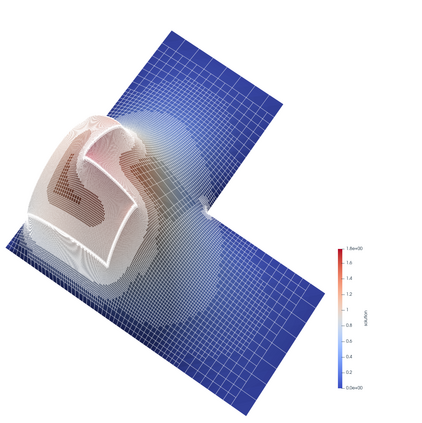
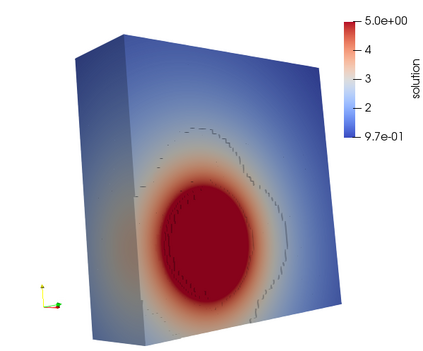
We propose an adaptive finite element algorithm to approximate solutions of elliptic problems whose forcing data is locally defined and is approximated by regularization (or mollification). We show that the energy error decay is quasi-optimal in two dimensional space and sub-optimal in three dimensional space. Numerical simulations are provided to confirm our findings.