High-dimensional Bayesian model selection by proximal nested sampling

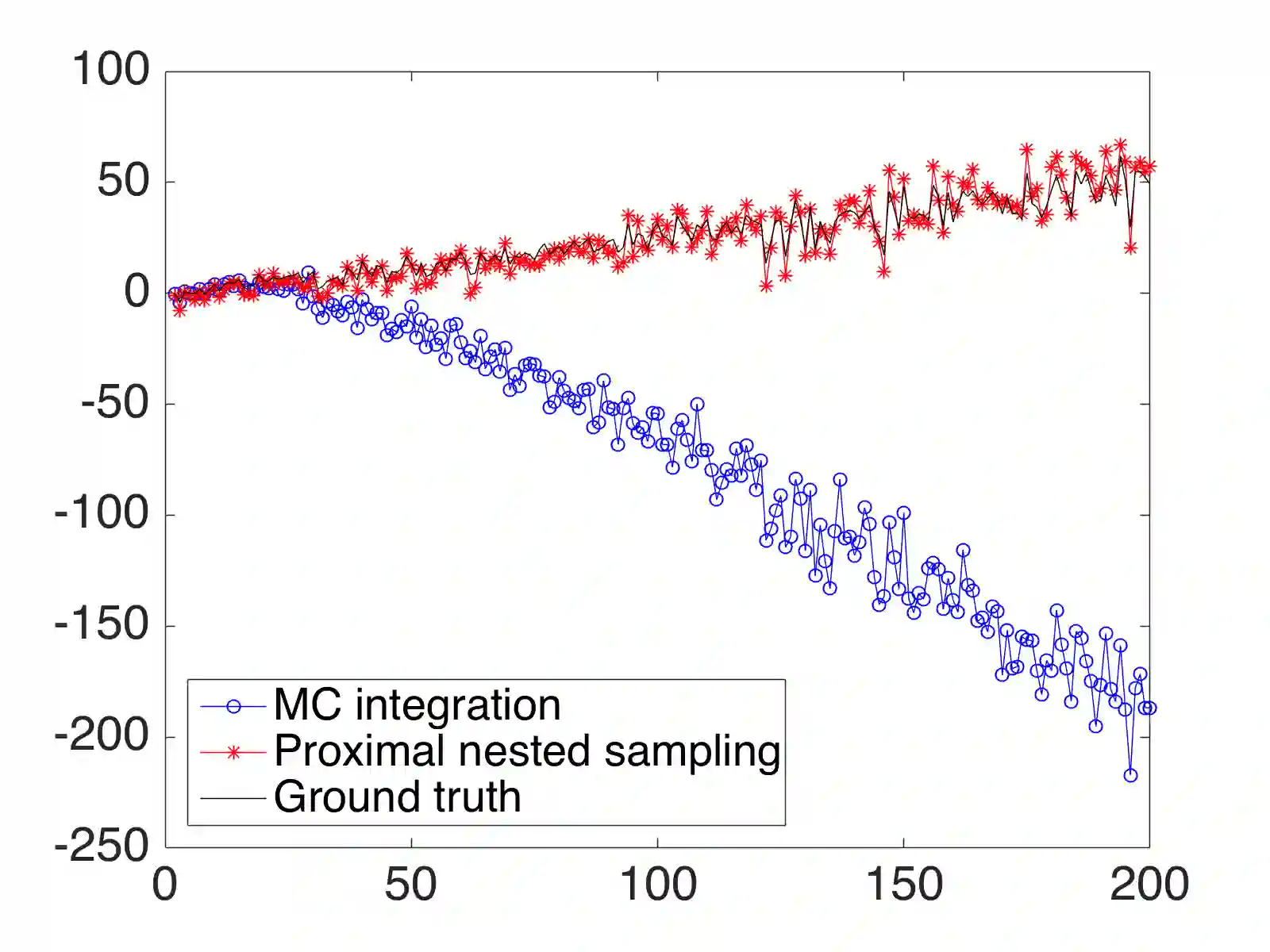
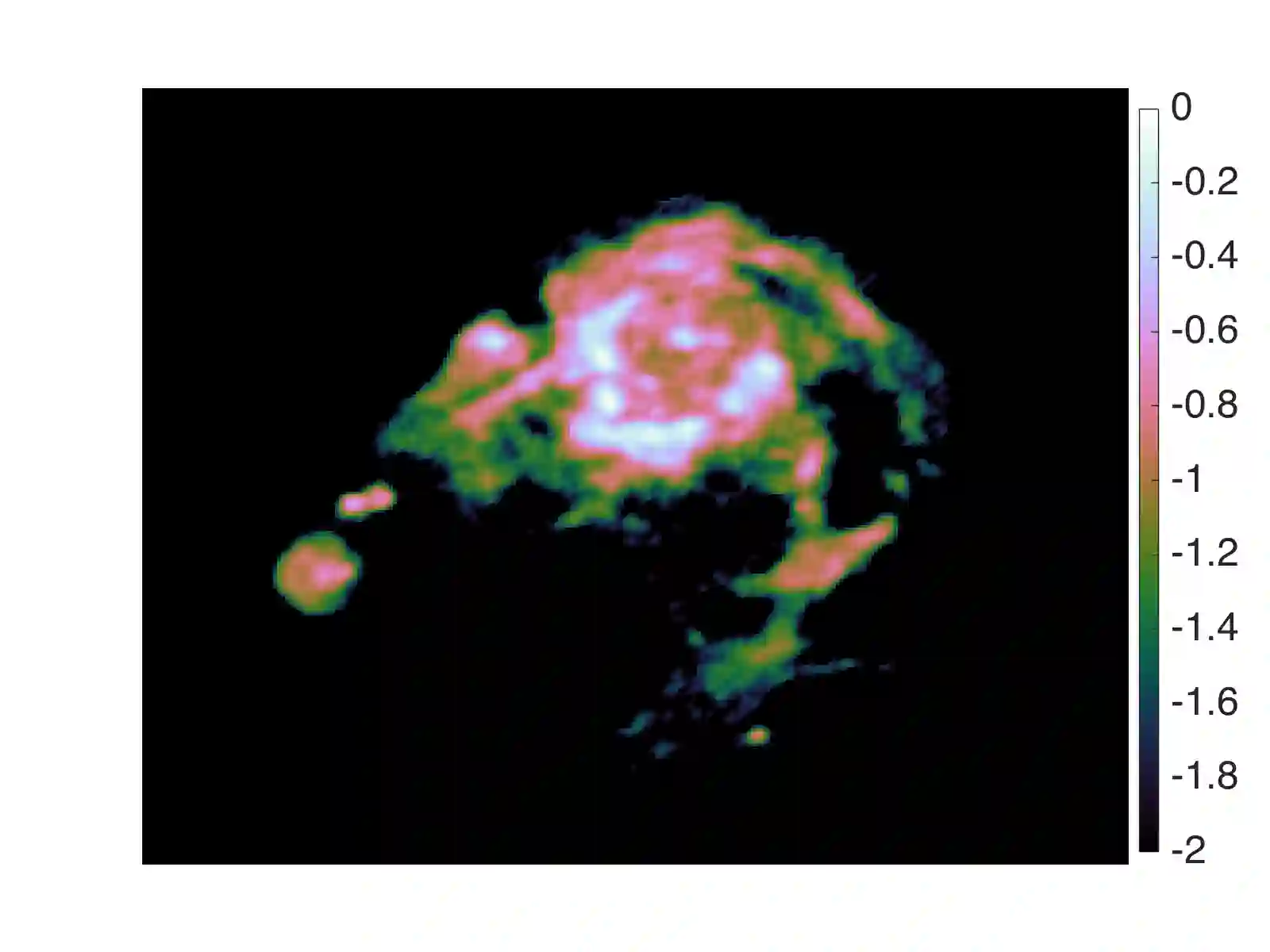
Imaging methods often rely on Bayesian statistical inference strategies to solve difficult imaging problems. Applying Bayesian methodology to imaging requires the specification of a likelihood function and a prior distribution, which define the Bayesian statistical model from which the posterior distribution of the image is derived. Specifying a suitable model for a specific application can be very challenging, particularly when there is no reliable ground truth data available. Bayesian model selection provides a framework for selecting the most appropriate model directly from the observed data, without reference to ground truth data. However, Bayesian model selection requires the computation of the marginal likelihood (Bayesian evidence), which is computationally challenging, prohibiting its use in high-dimensional imaging problems. In this work we present the proximal nested sampling methodology to objectively compare alternative Bayesian imaging models, without reference to ground truth data. The methodology is based on nested sampling, a Monte Carlo approach specialised for model comparison, and exploits proximal Markov chain Monte Carlo techniques to scale efficiently to large problems and to tackle models that are log-concave and not necessarily smooth (e.g., involving L1 or total-variation priors). The proposed approach can be applied computationally to problems of dimension O(10^6) and beyond, making it suitable for high-dimensional inverse imaging problems. It is validated on large Gaussian models, for which the likelihood is available analytically, and subsequently illustrated on a range of imaging problems where it is used to analyse different choices for the sparsifying dictionary and measurement model.