Revisiting 2-3 Red-Black Trees with a Pedagogically Sound yet Efficient Deletion Algorithm: The Parity-Seeking Delete Algorithm

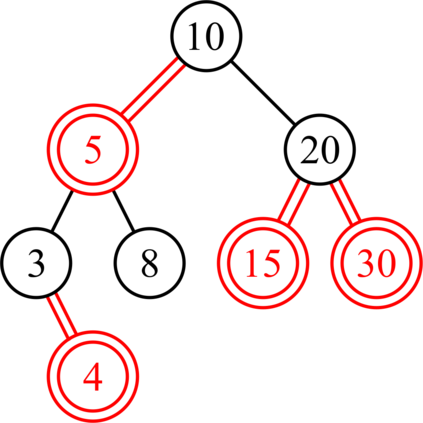
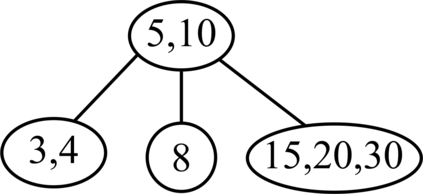
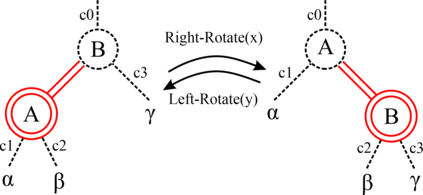
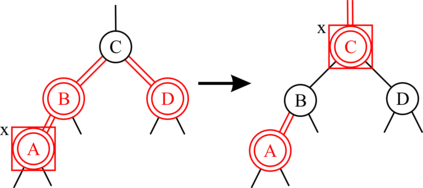
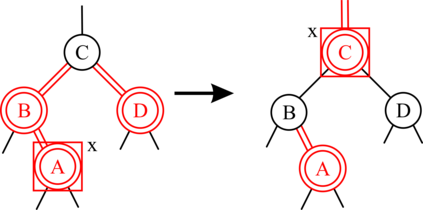
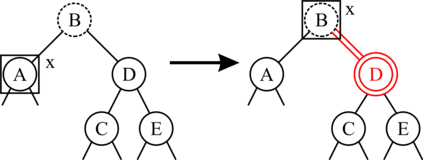
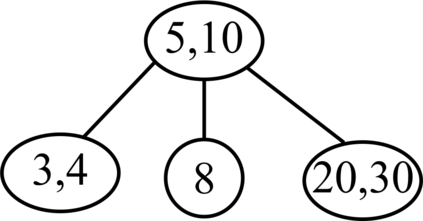
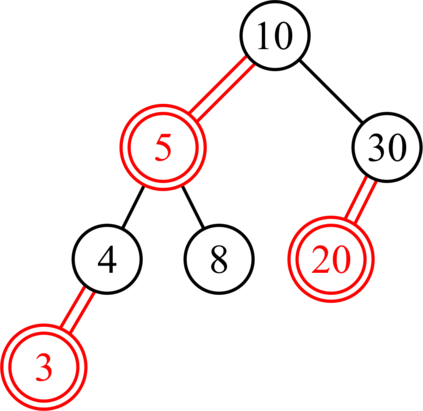
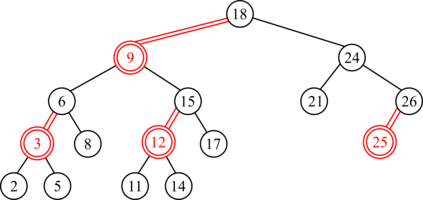
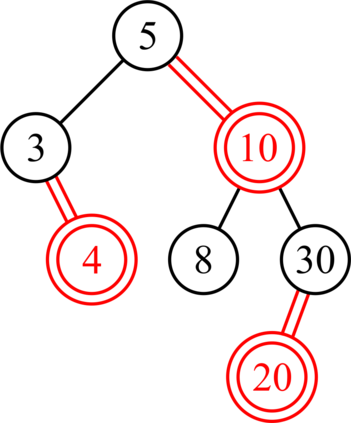
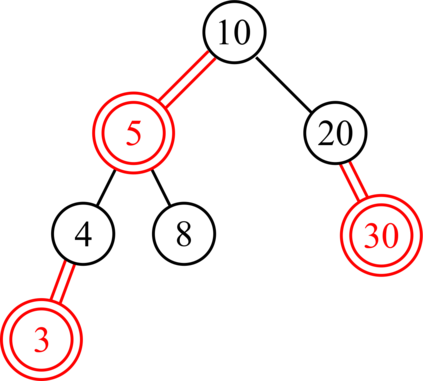
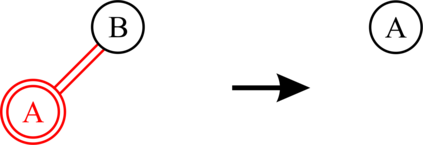
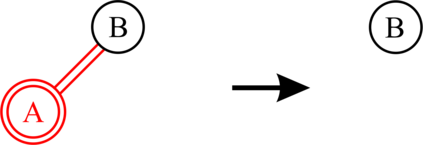
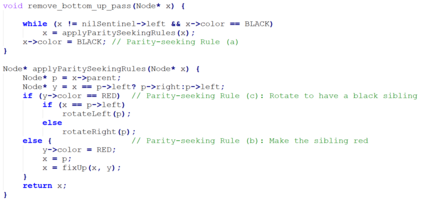
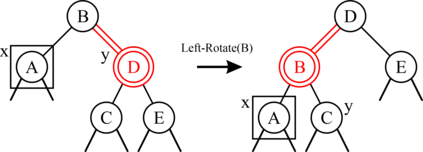
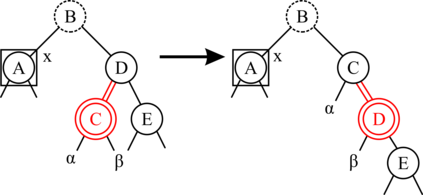Red-black (RB) trees are one of the most efficient variants of balanced binary search trees. However, they have always been blamed for being too complicated, hard to explain, and not suitable for pedagogical purposes. In the pioneering work of Guibas & Sedgewick (1978), both 2-3 and 2-3-4 variants of RB trees had been considered, but further study of the former had been abandoned due to the higher number of rotations in the insert algorithm. Sedgewick (2008) proposed a variant of 2-3 RB trees, viz. left-leaning red-black (LLRB) trees, in which red links are restricted to left children. He proposed recursive concise insert and delete algorithms. However, the top-down deletion algorithm of LLRB is still very complicated and highly inefficient. In this paper, we reconsider 2-3 red-black trees in which both children of a node cannot be red. We propose a parity-seeking delete algorithm with the basic idea of making the deficient subtree on a par with its sibling: either by fixing the deficient subtree or by turning the sibling deficient as well, ascending deficiency to the parent node. Interestingly, the proposed parity-seeking delete algorithm works for 2-3-4 RB trees as well. Our experiments show that, despite having more rotations, 2-3 RB trees are almost as efficient as RB trees and twice faster than LLRB trees. Besides, RB trees with the proposed parity-seeking delete algorithm have the same number of rotations and almost identical running time as the classical delete algorithm. While being extremely efficient, the proposed parity-seeking delete algorithm is easily understandable and suitable for pedagogical purposes.