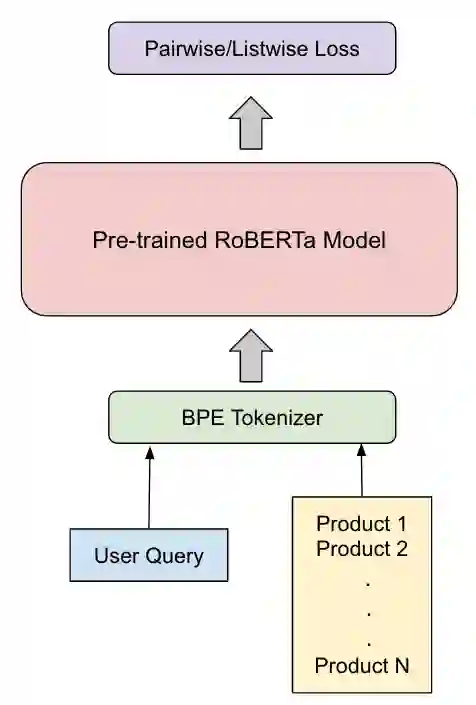
Efficient search is a critical component for an e-commerce platform with an innumerable number of products. Every day millions of users search for products pertaining to their needs. Thus, showing the relevant products on the top will enhance the user experience. In this work, we propose a novel approach of fusing a transformer-based model with various listwise loss functions for ranking e-commerce products, given a user query. We pre-train a RoBERTa model over a fashion e-commerce corpus and fine-tune it using different listwise loss functions. Our experiments indicate that the RoBERTa model fine-tuned with an NDCG based surrogate loss function(approxNDCG) achieves an NDCG improvement of 13.9% compared to other popular listwise loss functions like ListNET and ListMLE. The approxNDCG based RoBERTa model also achieves an NDCG improvement of 20.6% compared to the pairwise RankNet based RoBERTa model. We call our methodology of directly optimizing the RoBERTa model in an end-to-end manner with a listwise surrogate loss function as ListBERT. Since there is a low latency requirement in a real-time search setting, we show how these models can be easily adopted by using a knowledge distillation technique to learn a representation-focused student model that can be easily deployed and leads to ~10 times lower ranking latency.
翻译:高效搜索是电子商务平台的关键组成部分,该平台拥有无数的产品。 每天有数百万用户根据自己的需要搜索产品。 因此, 在顶端展示相关产品将提高用户经验。 在这项工作中, 我们提出一种新的方法, 将基于变压器的模型与各种列表式损失功能相结合, 用于电子商务产品排序。 我们预先用不同的列表损失功能, 将一个时装电子商务平台的 RoBERTA 模型培训成一个模型, 并使用不同的列表损失功能进行精细调整。 我们的实验表明, RoBERTA 模型与基于 NDCG的代理损失功能( aproxNDCG) 相比, 将提高NDCG 的13.9%, 比起 ListNET 和 ListMLE 等受欢迎的列表损失功能。 以 ExmlBERTA 模型为基础的ApproxNDCG RoBERTA 模型也实现了20.6%的改进。 我们称, 以最易端到端优化的方式直接优化 RoBERTA 模型, 以列表式的替代损失功能功能功能, 以列表化为 ListBERTERTERTERTERTA 格式进行搜索定位, 的功能将如何在实际定位上学习,,,, 以 一种低位 学习 的排序, 以 方法, 学习 以 以 的顺序显示 的顺序展示 方法,, 方法,, 学习,, 学习 以 学习 方法在 的 以 方法, 方法, 以 方法, 以 方法, 以 方法, 以 以 学习 的 以 的 的 的 的 以 方法以 方法以 方法在 学习 方式进行 学习 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 的 以 的 的 的 方式, 以 以 的 的 的 的 的 以 以 学习 学习 方式, 的 的 以 以 以 以 以 以 以 平流 学习 学习 方式进行 学习 更 平 的 的