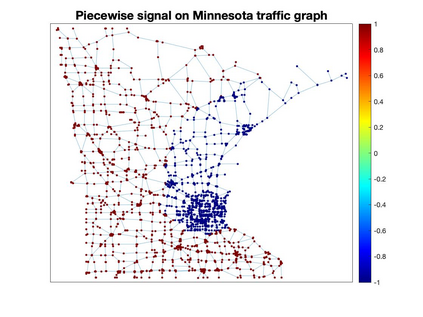
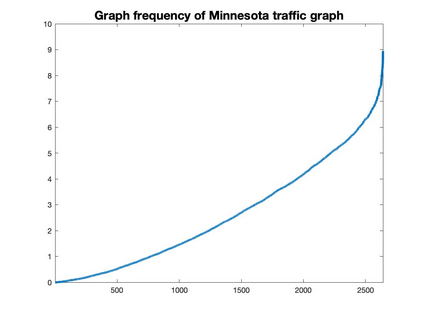
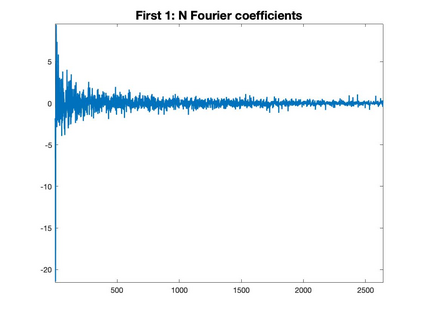
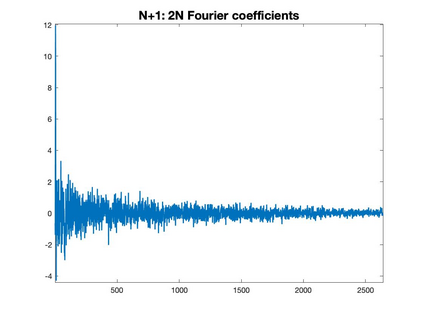
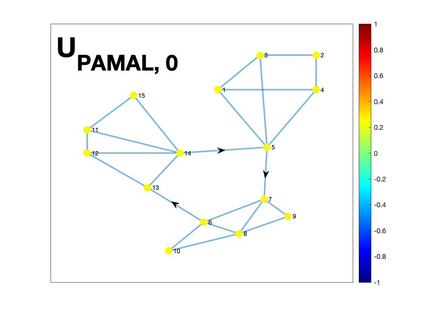
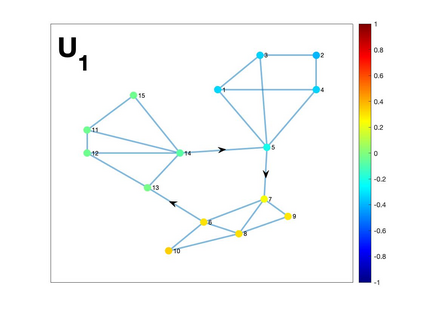
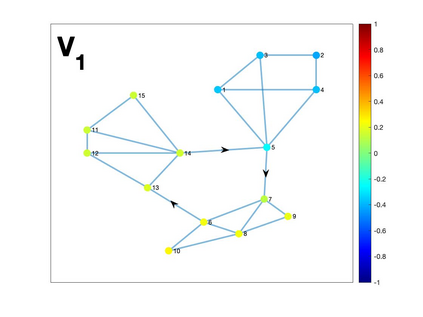
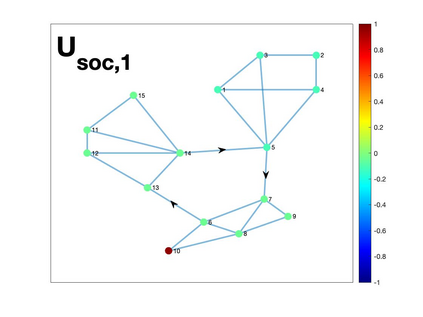
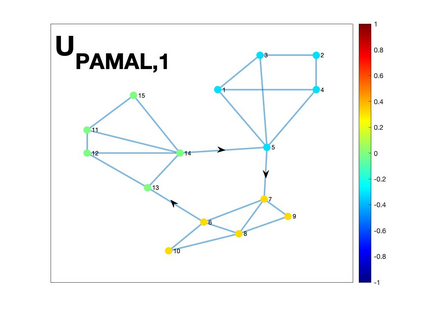
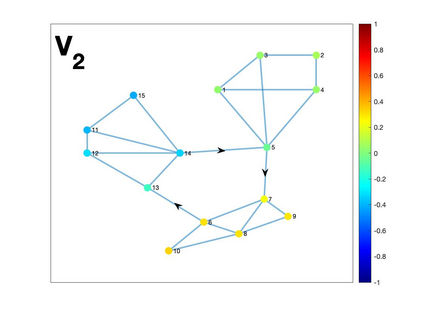
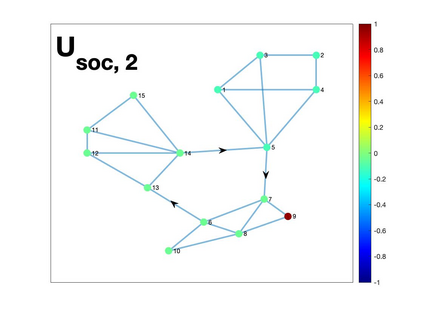
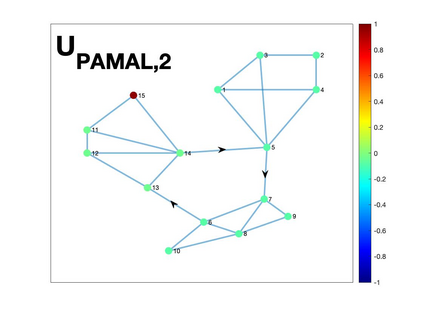
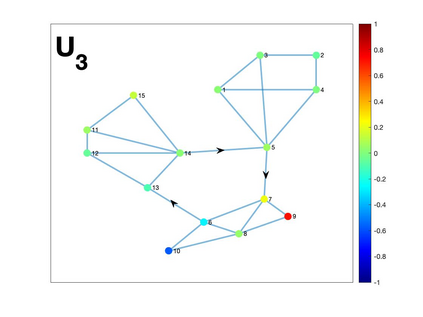
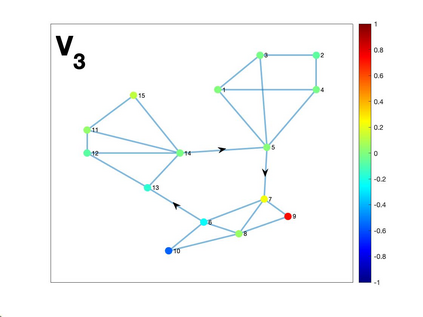
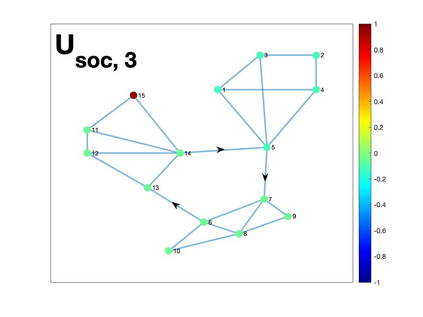
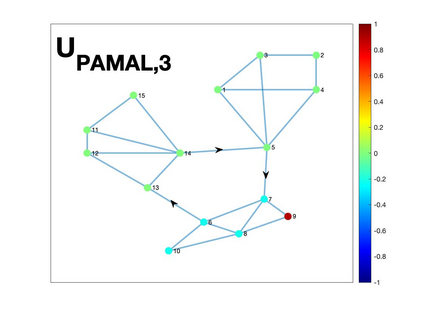
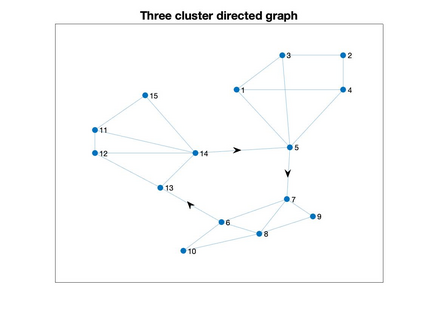
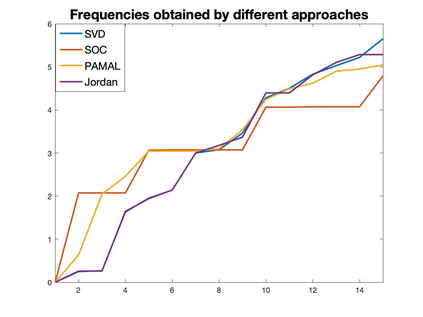
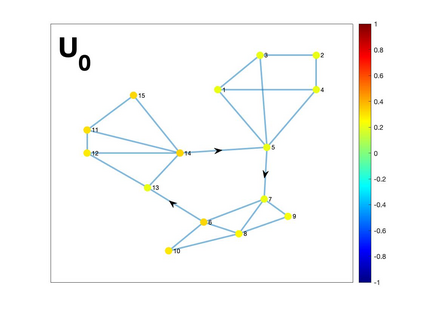
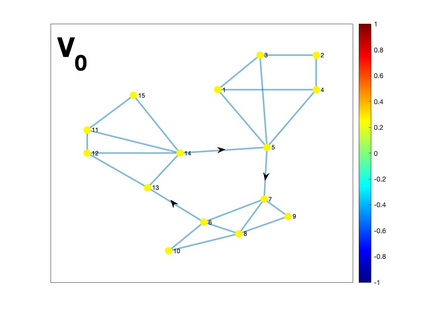
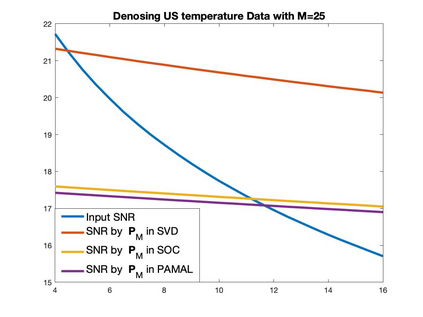
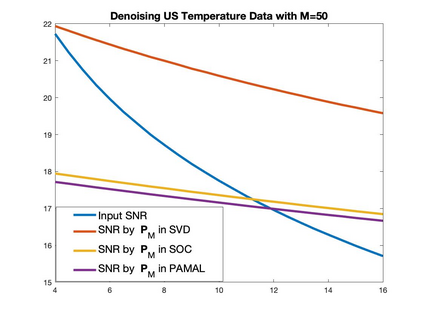
Graph Fourier transform (GFT) is a fundamental concept in graph signal processing. In this paper, based on singular value decomposition of Laplacian, we introduce a novel definition of GFT on directed graphs, and use singular values of Laplacian to carry the notion of graph frequencies. % of the proposed GFT. The proposed GFT is consistent with the conventional GFT in the undirected graph setting, and on directed circulant graphs, the proposed GFT is the classical discrete Fourier transform, up to some rotation, permutation and phase adjustment. We show that frequencies and frequency components of the proposed GFT can be evaluated by solving some constrained minimization problems with low computational cost. Numerical demonstrations indicate that the proposed GFT could represent graph signals with different modes of variation efficiently.
翻译:Fleier变换图(GFT)是图形信号处理的基本概念。在本文中,根据拉普拉西亚的单值分解,我们引入了定向图形上的GFT新定义,并使用拉普拉西亚的单值来表达图形频率的概念。提议的GFT占GFT的%。拟议的GFT与无定向图形设置中的常规GFT相一致,在定向环球图上,拟议的GFT是古典离散的Fourier变换法,直至某些旋转、变换和阶段调整。我们表明,可以通过以低计算成本解决某些受限的最小化问题来评估拟议的GFT的频率和频率组成部分。数字演示表明,拟议的GFT可以高效地代表不同变异模式的图形信号。