A closed form scale bound for the $(ε, δ)$-differentially private Gaussian Mechanism valid for all privacy regimes

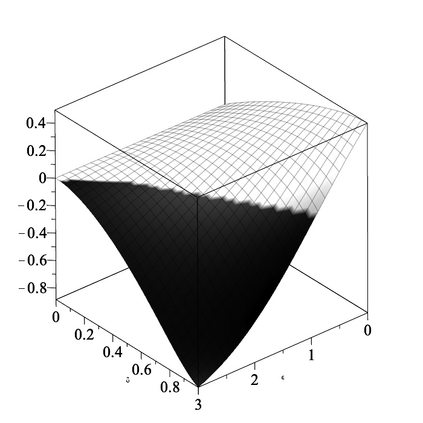
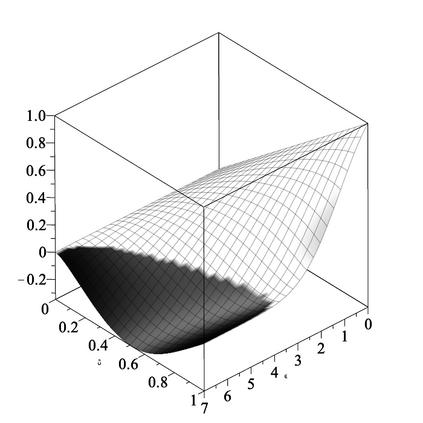
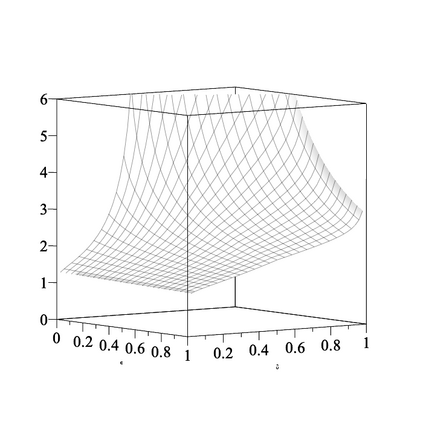
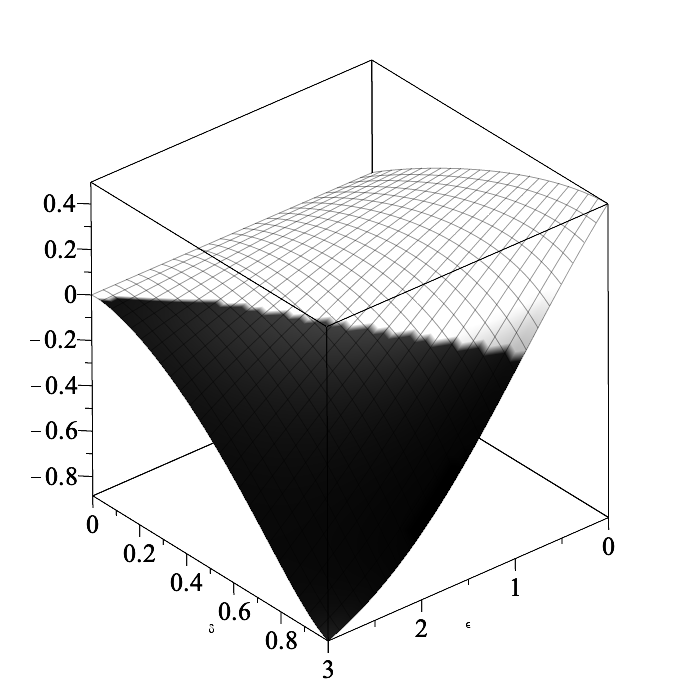
The standard closed form lower bound on $\sigma$ for providing $(\epsilon, \delta)$-differential privacy by adding zero mean Gaussian noise with variance $\sigma^2$ is $\sigma > \Delta\sqrt {2}(\epsilon^{-1}) \sqrt {\log \left( 5/4\delta^{-1} \right)}$ for $\epsilon \in (0,1)$. We present a similar closed form bound $\sigma \geq \Delta (\epsilon\sqrt{2})^{-1} \left(\sqrt{az+\epsilon} + s\sqrt{az}\right)$ for $z=-\log(4\delta(1-\delta))$ and $(a,s)=(1,1)$ if $\delta \leq 1/2$ and $(a,s)=(\pi/4,-1)$ otherwise. Our bound is valid for all $\epsilon > 0$ and is always lower (better). We also present a sufficient condition for $(\epsilon, \delta)$-differential privacy when adding noise distributed according to even and log-concave densities supported everywhere.