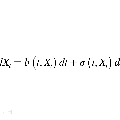电磁兼容仿真不确定性定量分析方法研究

项目名称： 电磁兼容仿真不确定性定量分析方法研究

项目编号： No.51477036

项目类型： 面上项目

立项/批准年度： 2015

项目学科： 电工技术

项目作者： 王立欣

作者单位： 哈尔滨工业大学

项目金额： 84万元

中文摘要： 使用确定性模型来表征具有不确定性的物理过程是影响仿真可信度的重要因素。本项目旨在构建电磁兼容仿真不确定性定量分析方法，首先获取随机参数的统计特性，然后使用广义多项式混沌方法求解随机物理方程来进行不确定性的传递分析。将解决的关键技术问题包括：1）采用主成分分析及K-L展开并结合自适应技术解决多参数分析带来的维数灾难问题；2）用映射方法解决三维数值仿真中几何参数的不确定性带来的求解域的不稳定问题；3）使用多元广义多项式混沌方法解决具有任意分布的不确定性参数的分析问题；4）利用拓展的FSV方法对所提出的不确定性分析方法进行有效性验证。通过本项目的研究探索参数不确定性对EMC仿真结果的影响机制，求解随机传输线方程和随机麦克斯韦方程，赋予仿真结果一定的不确定度，增加仿真的可信度。

中文关键词： 电磁兼容；仿真不确定性；多项式混沌方法；随机微分方程

英文摘要： It is common practice to characterize the physical process with uncertainty using a deterministic model, which may affect the credibility of simulations. So the project is proposed to construct a quantitative uncertainty analysis method of EMC simulations. After get the statistical properties of random parameters, the generalized polynomial chaos method is applied to solve stochastic physical equations which represent the transfer process of uncertainty in the simulation. The key issues addressed include: 1) using the Principal Component Analysis and K-L expansion combined with adaptive techniques to solve the curse of dimensionality problem caused by multiple random variables; 2) using mapping technique to solve random domain problem brought about by the uncertain geometry in three-dimensional numerical simulations; 3) using multi-element generalized polynomial chaos method to analysis the uncertainty introduced by parameters with random distributions; 4) using extended FSV method to validate the proposed uncertainty analysis method. The main aim of this project is to explore the influencing mechanism of parameter uncertainty on the results of EMC simulation. By solving the stochastic transmission line equations and the stochastic Maxwell's equations, simulation results are presented with quantitative uncertainty, which enhances the credibility of simulations.

英文关键词： EMC;Uncertainty of simulations;Polynomial chaos method;Stochastic differertial equation