基于非整数阶梯度的稀疏信号重构方法研究

项目名称： 基于非整数阶梯度的稀疏信号重构方法研究

项目编号： No.11201366

项目类型： 青年科学基金项目

立项/批准年度： 2013

项目学科： 数理科学和化学

项目作者： 李科学

作者单位： 西安交通大学

项目金额： 22万元

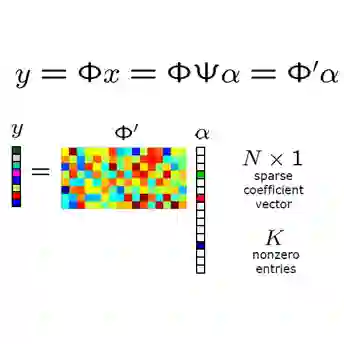
中文摘要： 稀疏信号重构是压缩感知理论中的核心问题。现有的重构算法大多是基于优化1-范数而发展起来的，因而存在数据的大量冗余难以去除、稀疏系数尺度的位置难以区分等不足，因此，通过优化 p-范数（p<1）是必然选择。但是，p-范数优化问题是非凸的，如何对其进行有效求解仍是个公开性问题。 因此, 发展针对 p-范数优化问题的数学理论与方法具有重要的理论意义和应用价值。本项目旨在运用分数阶微积分理论，基于"一个在整数阶微积分框架下的非凸优化问题在分数阶微积分框架下可以是凸的"这一理念，通过引入非整数阶梯度这一概念，拓展凸函数的概念, 提出一种基于非整数阶梯度的求解 p-范数优化问题的方法，从而为稀疏信号重构问题的研究探索出一种全新的理论和方法。

中文关键词： 稀疏信号；压缩感知；非整数阶梯度；重构算法；

英文摘要： Sparse signal reconstruction is the central issue of Compressed Sensing. The existing reconstruction algorithms have mostly concentrated on the 1-norm optimization, which leads to lots of redundant and it is difficult to distinguish between the location of the sparse coefficient scale. Hence, it is an inevitable choice to consider the p(p&lt;1)-norm optimization. However, the p-norm optimization problem is non-convex and it is well-known that how to solve non-convex optimization problems is an open problem. Therefore, developing the mathematical theory and computational methods for p-norm optimization has important theoretical significance and application value. Based on the concept that &quot;A non-convex optimization problem in the framework of integer order calculus is probably a convex optimization problem in the framework of fractional calculus&quot;, this project aims at using fractional calculus theory to introduce the notion of non-integer order gradient to generalize the concept of convex function and to develop a method to solve the p-norm optimization problem based on the non-integer order gradient. Thus, a new kind of theory and methods for sparse signal resconstruction is developed.

英文关键词： sparse signal；compressed sensing；non-integer order gradient；reconstruct algorithm；