数据科学家需要了解的5种聚类算法

会员服务 ·

数据科学家需要了解的5种聚类算法

2018 年 5 月 3 日 Datartisan数据工匠 George Seif

点击上方

Datartisan数据工匠

可以订阅哦！

聚类是一种将数据分组的机器学习技术。给定一组数据，我们能够利用聚类算法把每个数据点分到特定的组别内。理论上而言，同组的数据点应该有类似的性质，而且不同组的数据点应该差别很大。聚类是一种非监督学习方法，也是统计数据分析中广泛应用的技巧。

数据科学中，我们能够利用聚类分析进行数据分组，并且从分组中得出数据的内在信息。今天，我们将要介绍数据科学家学要了解的5个主流聚类算法以及它们的利弊。

K均值聚类 (K-Means Clustering)

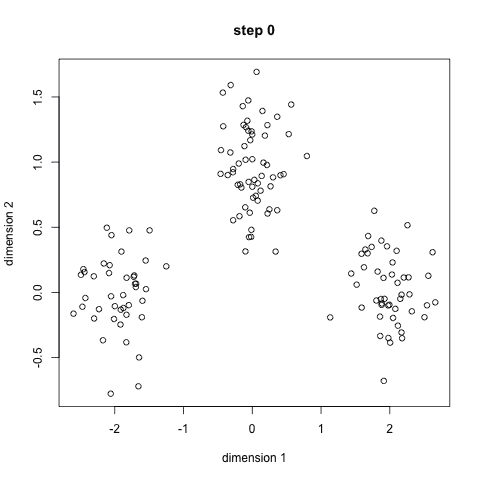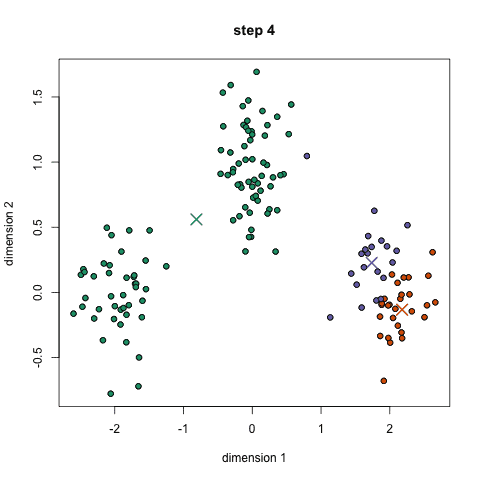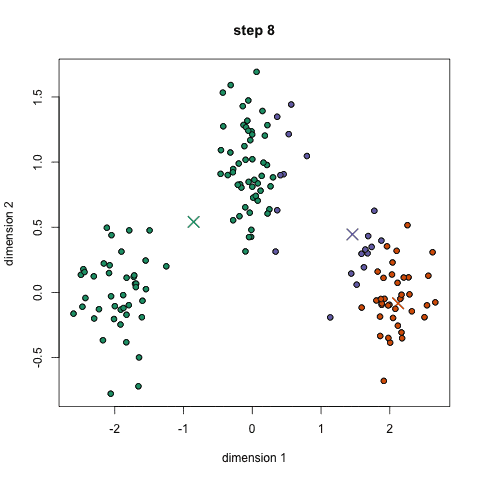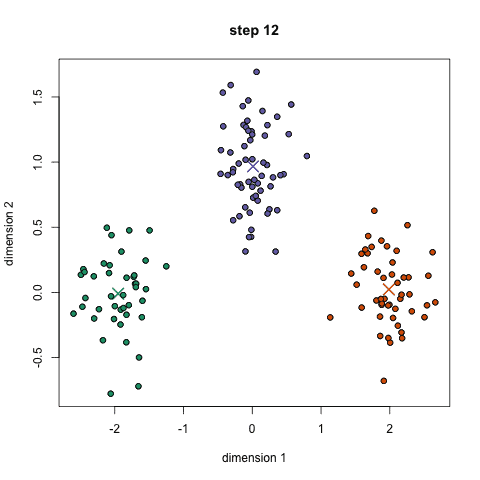
k均值聚类是最常见的聚类算法，常常出现在机器学习以及数据科学的入门教程中。很容易理解，并且代码实现也很简洁。下面的图是一个简单的示例：

首先，我们设定组数，并且随机初始化各组的中心。为了确定分组的个数，可以简单的浏览数据或者作图来检查有多少个明确的分组。中心点拥有和数据点相同的维度。
每个数据点通过计算其与各组中心的距离，并且会分类到距离最近的组别。
基于这些已分类的数据点，我们重新计算各组的中心，也就是各组别的所有数据点的均值。
重复这些步骤一定迭代次数，或者直到各组的中心点收敛。你也可以选择多次地随机初始各组的中心，然后保留最好的结果。

另一方面，k均值方法也有一系列的缺点。首先，你必须设定组别的数量。这对于一个聚类算法而言存在弊端，因为我们想让算法根据数据自己决定合适的组别数量。K均值法也需要对组均值进行随机初始化，这很有可能会导致不同的聚类结果。因此，聚类结果不具备一致性和重复性。其他的聚类方法更具有一致性。

K中位数是与K均值类似的聚类算法，唯一的差别在于我们每次迭代中计算的是各组的中位数点而不是均值点。这个方法对离群值更稳健，对于大数据集计算速度会更慢，因为每次迭代的计算量也很大。

均值漂移算法

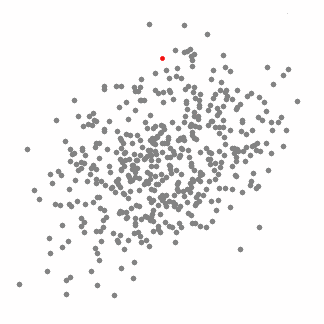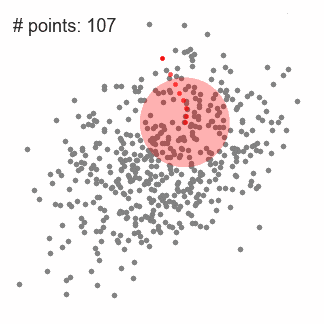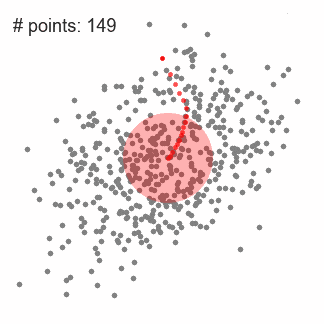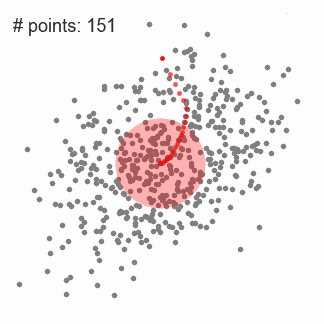
均值漂移算法是一个基于滑动窗口的算法，为了寻找数据点密集的区域。这是一个基于中心的算法，也就是为了定位出各组的中心点。算法是通过不断地更新中心点的候补点，每个候补点都是滑动的窗口内的点均值。这些候补点的窗口接下来会按照类似的过程进行迭代，最后除去附近的副本，构成最终的中心点以及它们对应的分类。下图是一个简单的示例：

为了解释均值漂移，我们考虑上图的二维空间的一组点。我们从一个定位在C点（随机选择）的窗口开始，并且以r为半径。均值漂移是一个爬山算法，不断地把它的核移动到更高密度的区域，直到收敛。
在每次的迭代中，滑动窗口都会移向数据点更密集的地方，实质上是把中心点移到当前迭代中的滑动窗口内的数据点的均值上。滑动窗口的密度正比于包含的点的数量。自然地，把中心点移到窗口内的均值点上，会让中心点逐步地往高密度的区域移动。
我们不断地移动窗口，知道我们不能够通过移动来包含更多的数据点。观察上图，我们一直在更新中心点，知道无法再增加点密度。
重复1-3步，直到所有点都落在某个窗口内。如果有几个窗口有重叠，就保留具有更高密度的窗口。各个数据点就会被分类到其所属的窗口内。

整个聚类过程如下图所示。每个黑色点代表滑动窗口的中心，灰色代表数据点。

与K均值聚类不同在于，我们不需要选择类别的个数，因为均值漂移算法能够自动识别组别个数。这是一个很大的好处。聚类的中心更倾向于有高密度的数据点区域，这也是个非常好的特性，因为从数据的角度出发这很符合直觉。缺点在于窗口大小的确定，也就是半径r的选择，不是很显然。

基于密度的空间聚类（DBSCAN）

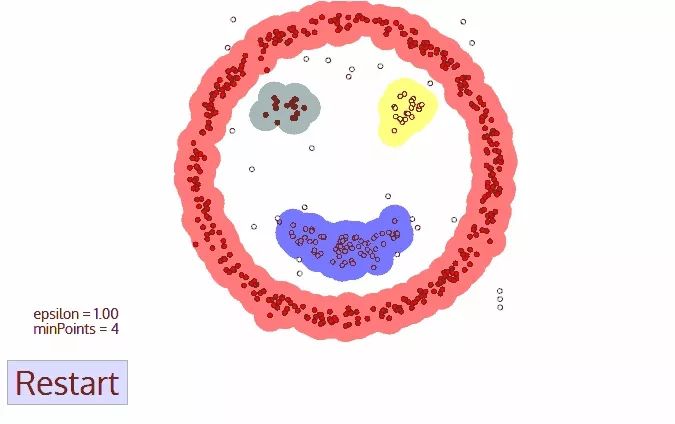
DBSCAN是一种基于密度的聚类方法，类似均值漂移，但是有很多显著的优点。我们从下图图示开始着手：

DBSCAN从一个任意的数据点开始，这个数据点的近邻点通过距离识别出来（所有在距离内的点都是近邻点）。
如果在一个点的周围有足够数量的近邻点（以设定的MinPoints值作为阈值），聚类过程就会开始，并且当前的数据点就会成为新的类别中的第一个点。否则，这个数据点就会被标记为噪声点（有可能在后面的部分，它会属于某个类别）。以上任意两种情况都会被标记为“已遍历”。
对于新类别中的第一个点，这个点的近邻点也属于同一类别，并且不断重复地将该类别内的近邻点融入同一个组。
重复第2、3步，直到所有的点都被遍历，并且对于当且类别给出标签。
一旦我们完成了当前类别的聚类，一个新的未被遍历的点会被选择并且重新开始以上过程，探索新的类别或者噪声。重复这个过程直到所有点都被遍历。因为所有点都被遍历，所以每个店都会有对应的分类标签或者变为“噪声”。

DBSCAN相比其他分类算法展现了很多优点。首先，它不需要提前设定组别数量。它也能够识别出噪声，而不像均值漂移那样简单地也对噪声进行聚类。除此之外，它也能够很好地找出任意大小任意形状的类别。

DBSCAN的主要缺陷在于，当类别的密度变化很大时，它表现的不太好。这是因为预设的阈值距离以及minPoints，在识别近邻点的过程中会因为密度的变化而将一个类别拆分为多个类别。这个缺点也会出现在高维数据的分析中，因为距离阈值很难给出合适的估计。

EM聚类算法，使用高斯混合模型

EM聚类算法，使用高斯混合模型（GMM）

K均值聚类的一个缺点在于它简单地使用了均值作为聚类中心。我们可以通过下图来阐述为什么这种选择不好。左边很明显能够分别出两个圆形的类别具有不同的半径，但是它们的均值相同。K均值不能够解决这个问题，因为不同类别的均值很相近。当类别不是圆形的时候，K均值法也没法很好地处理。

高斯混合模型 (GMMs) 比K均值模型更适用。我们假设数据点是高斯分布的；这个假设比直接定义它们是有固定原点的圆形更宽松。这样，我们就有两个参数来形容类别的形状：均值和标准差！考虑二维的例子，这意味着类别可以是任意形状的椭圆（因为我们在x,y两个维度都具有标准差）。因此每个高斯分布对应着一个单独类别。

为了寻找每个类别的高斯分布的参数，我们利用一种优化算法叫做期望最大化（EM算法）。下图展示了用来拟合数据的高斯分布。接下来我们继续讨论对混合高斯模型使用EM算法聚类的过程。

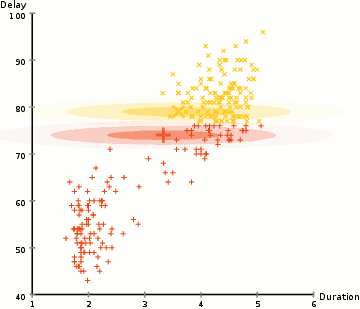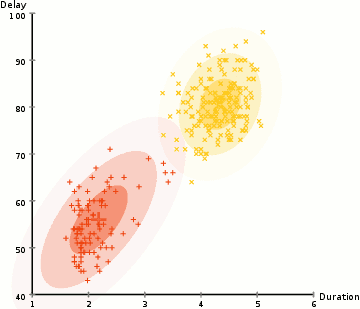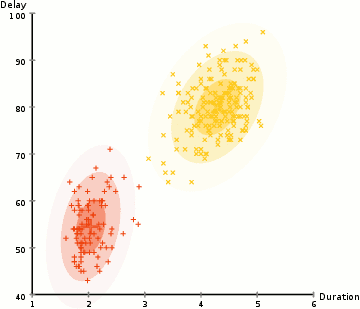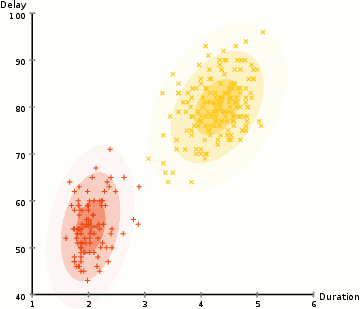
我们开始设定类别数量并且对于每个类别，随机初始化对应的高斯参数。你也可以通过观察数据大致猜测各个参数，但这并不必要。因为即使初始化的参数很糟糕，算法也可以很快地收敛。
给出每个类别的高斯分布，计算每个数据点属于特定类别的概率。一个点距离高斯的中心越近，那么它属于该类别的概率越大。对于高斯分布而言，这很符合直觉，因为绝大多数点都分布在它的均值附近。
基于计算出的概率，我们计算一组新的高斯参数。为了计算参数，我们最大化使每个类别的数据点的概率。我们计算过程中，使用了数据点的加权求和，其中权重是每个数据点属于特定类别的概率。为了直观解释，我们可以参考上图，并且以黄色类别为例。在第一步迭代中，这个分布的参数是随机初始化的，但是我们看到大多数黄色的点在分布的右侧。当我们计算加权求和时，即使有一些点在在中心附近，但是大多数都在右侧。因此，分布的均值很自然地向右移动。我们也能看到大多数点分布在右上和左下。因此标准差也会类似地变化，为了形成一个椭圆来拟合这些数据点，同时也最大化这个加权求和。
重复第2、3步直到收敛，也就是分布的参数不再改变。

使用高斯混合模型时有两个有点。首先，GMMs因为考虑了类别的相关性，比K均值更稳健；考虑了标准差，能形成任意椭圆形状的类别。K均值是GMMs的一种特殊情况，当类别之间的协方差接近0的时候，GMMs就等价于K均值法。第二，因为GMMs使用了概率，每个数据点都有很多个类别。所以如果一个数据点处于两个类别的重叠部分，我们能够简单地定义它的类别组成，百分之X是类别1，百分之Y是类别2 。也就是说，GMMs支持混合成分。

合成聚类

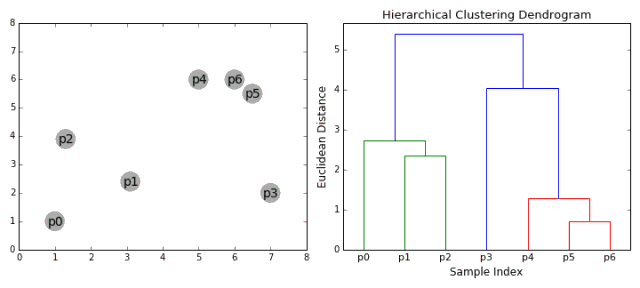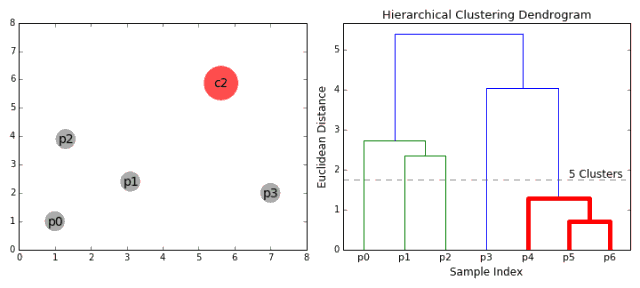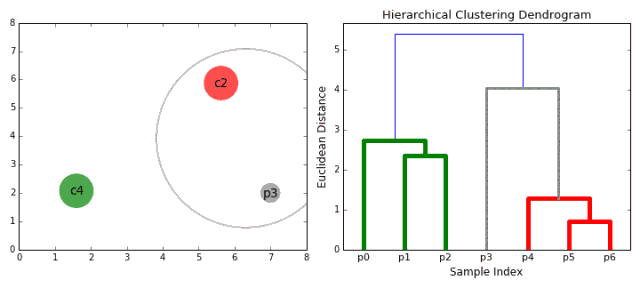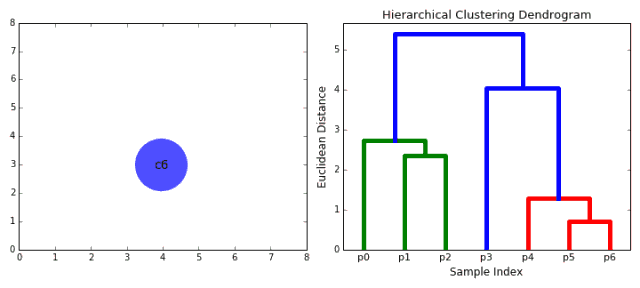
层次聚类法通常分为两类：自上而下和自下而上。自下而上是把每个数据点当成单独一类，然后不断地融合不同的类别，直到所有类别融合到一个包含所有数据点的类别。自下而上的层次聚类因此也被称为合成聚类。类别的层次一般以树的形式展示。树的根是包含所有样本的类别，叶是只有一个样本的类别。下图展示了整个聚类过程：

我们开始把每个数据点都当做单独的类别，如果有X个数据点，我们就有X个类别。我们接下来选择一个距离来度量两个类别间的距离。比如，我们可以使用平均链接 (average linkage)，平均链接定义为两个类别中所有数据点的平均距离。
每次迭代中，我们把两个类别合并在一起。选择平均链接最小的两个类别进行合并。根据我们选择的距离，拥有最小距离的两个类别一定是最相似的，因此可以合并在一起。
重复第二步，直到我们打到树的根部，也就是所有数据点都包含于一个类别之内。最终，我们可以选择想要的类别数量，只要选择停止合并的位置，也就是我们停止继续构建树的位置。

层次聚类不需要我们预设类别数量，我们甚至可以在最后选择我们想要的类别数目。而且，这个算法对度量距离的选择很不敏感，几乎相差无几，但是对其他的聚类算法而言，度量的不同会导致聚类结果的不同。层次聚类适用于具有层次结构的数据，并且你想要找出数据的层次结构；其他的算法不能达到这个目的。层次聚类的这些优点同时也带来了较低的效率，因为它的时间复杂度是，远高于K均值和GMM的线性复杂度。

结论

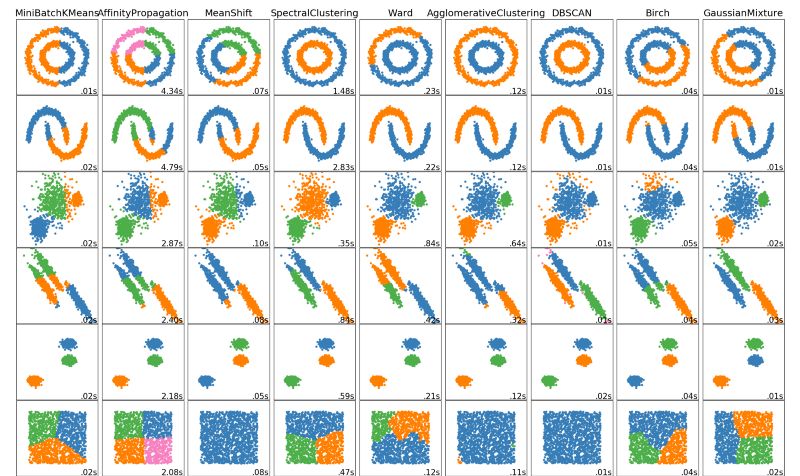
以上便是一个数据科学家需要了解的5个聚类算法。我们最后展示一个精美的聚类算法的可视化总结，来自于Scikit Learn。