最新《高斯过程回归简明教程》，19页pdf

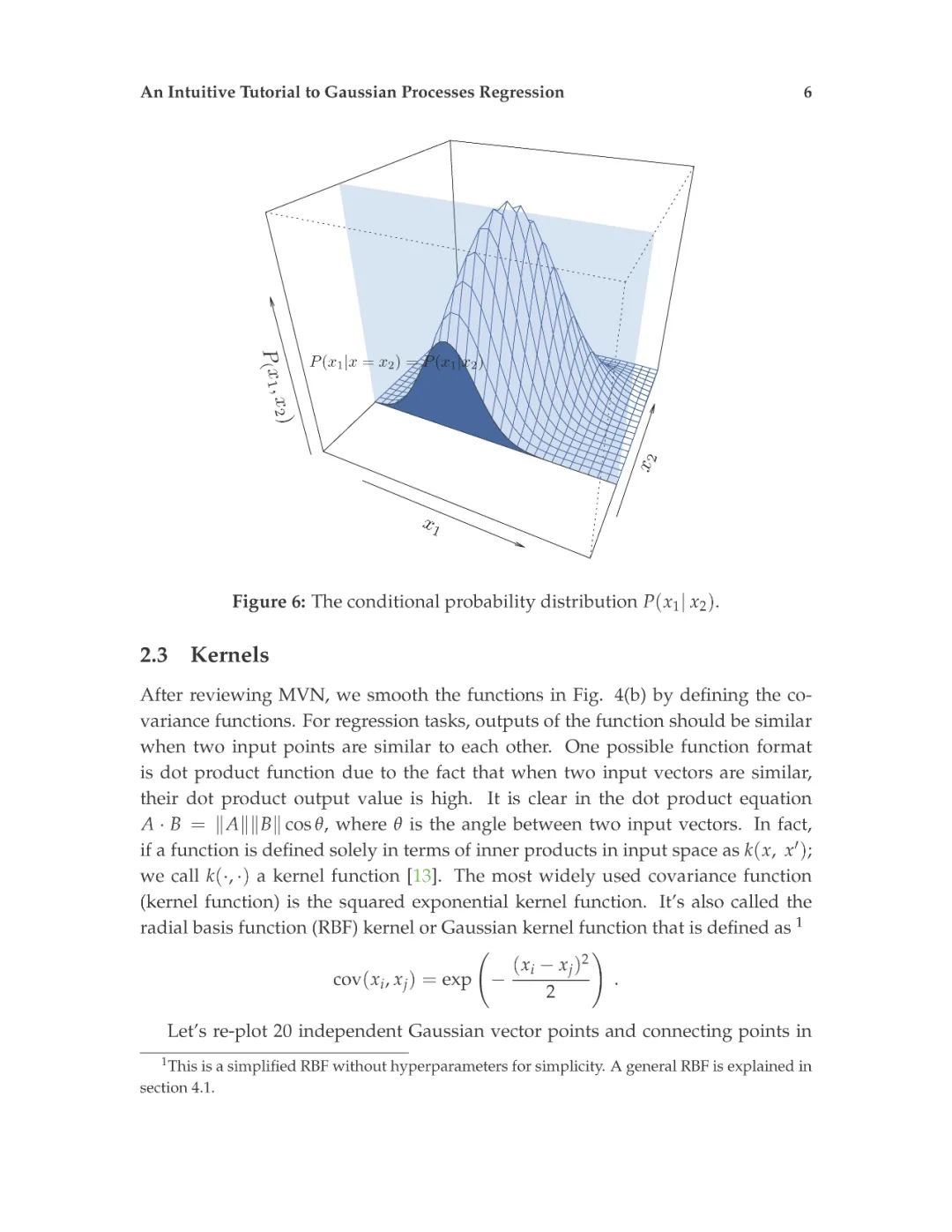
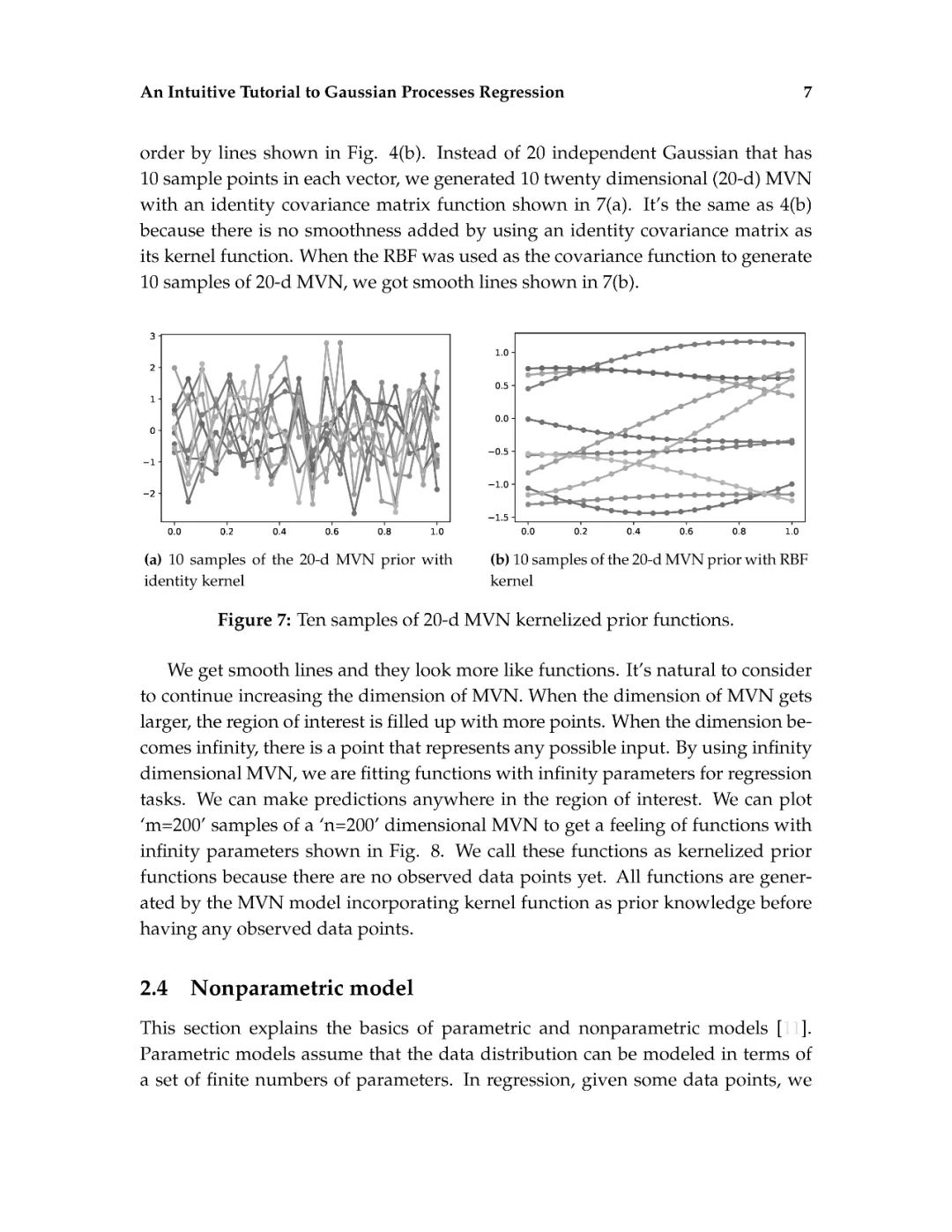
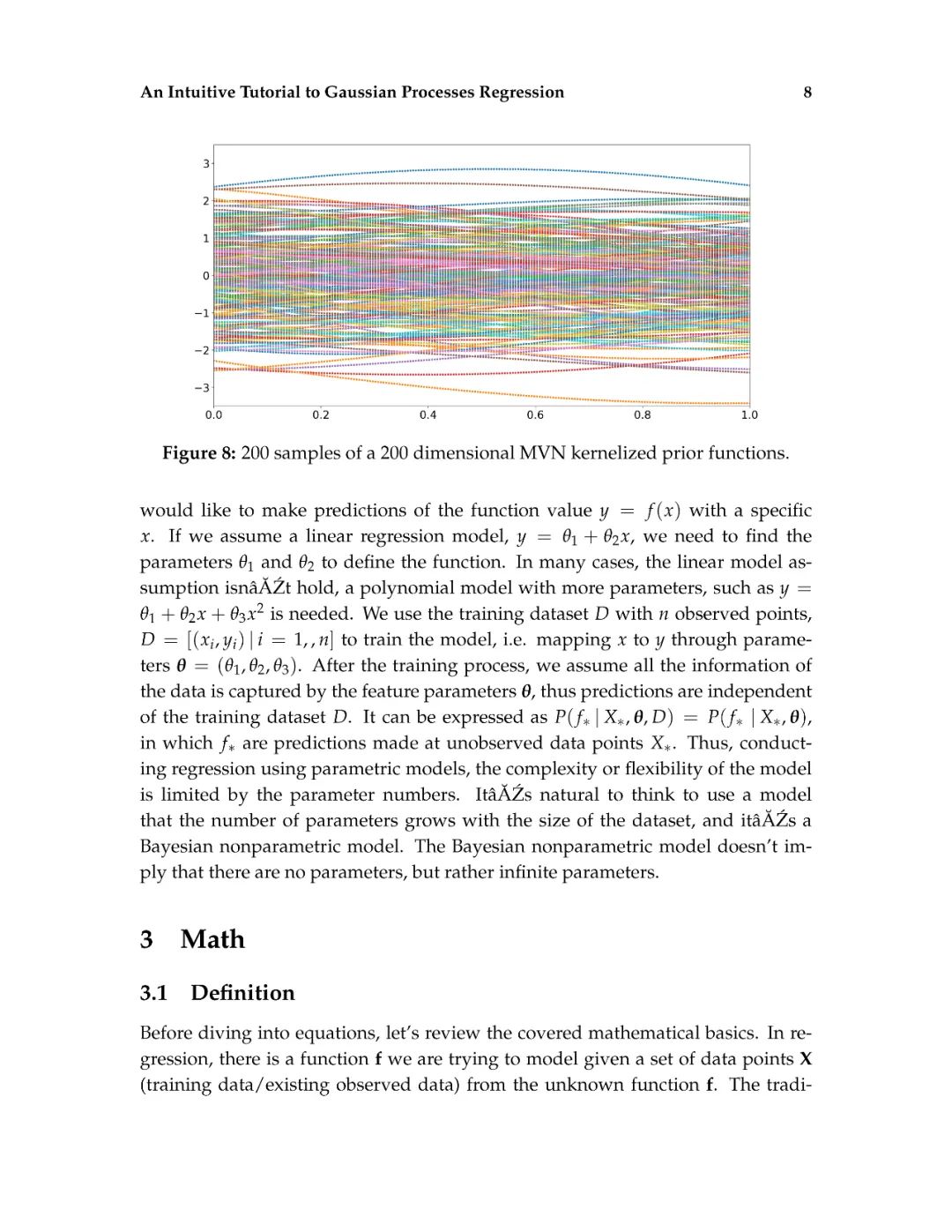
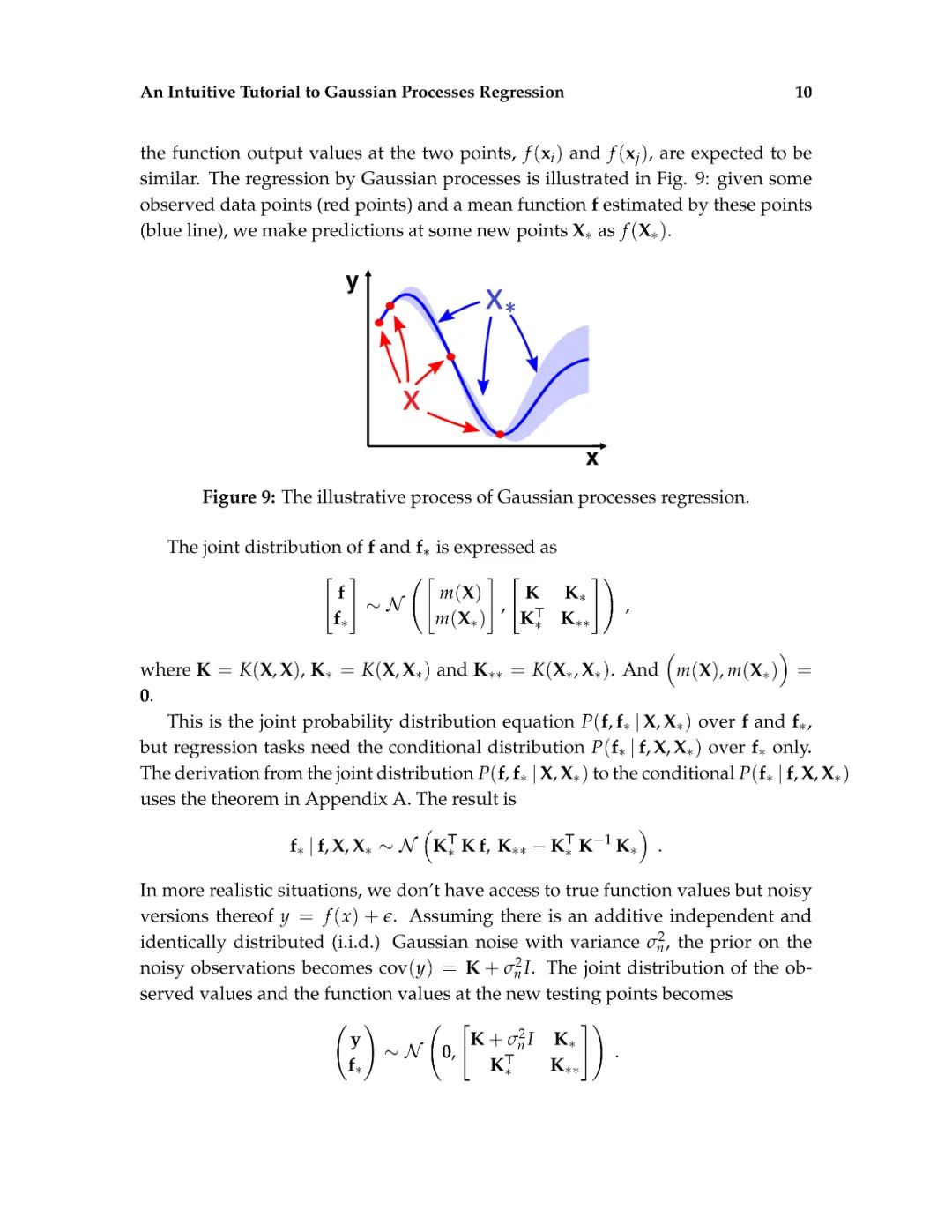
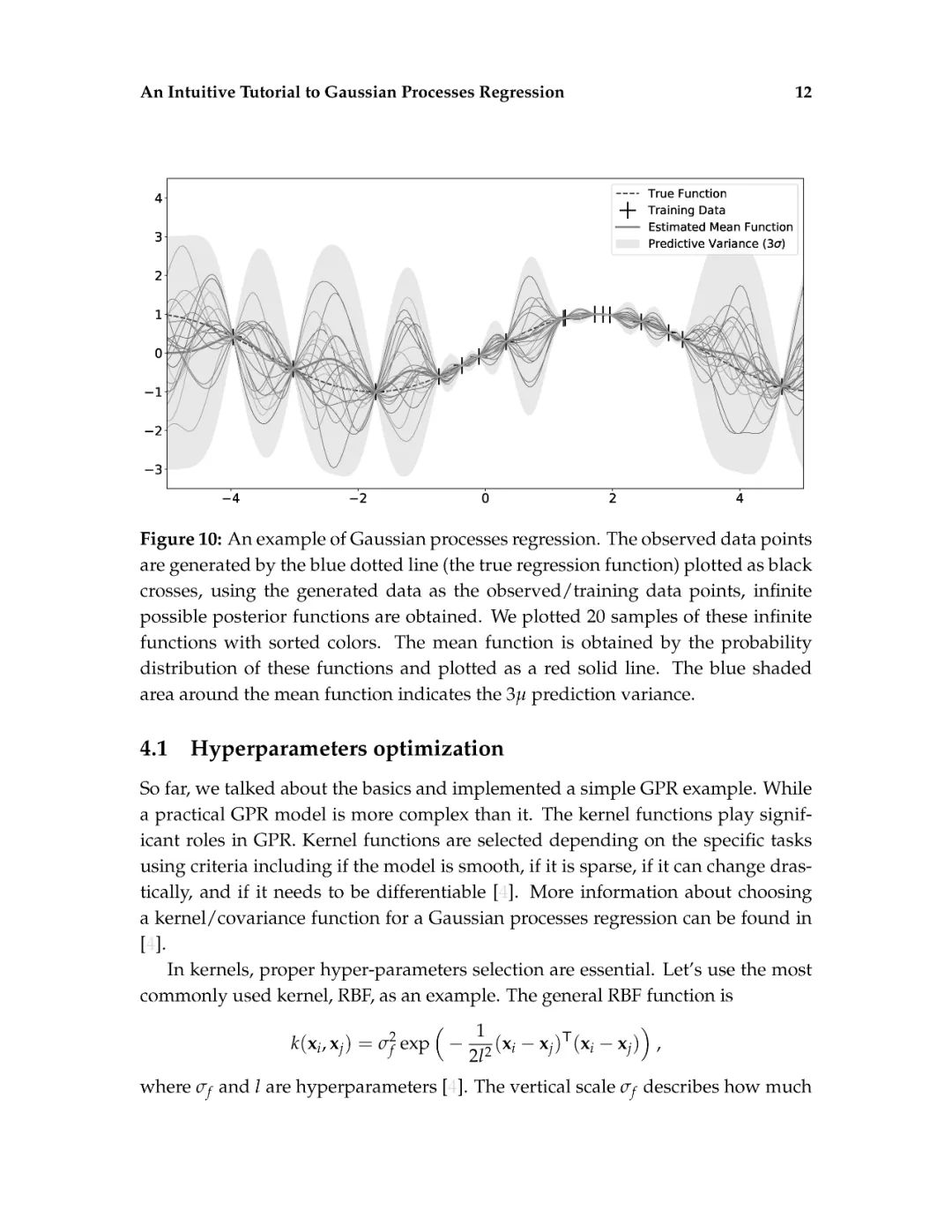
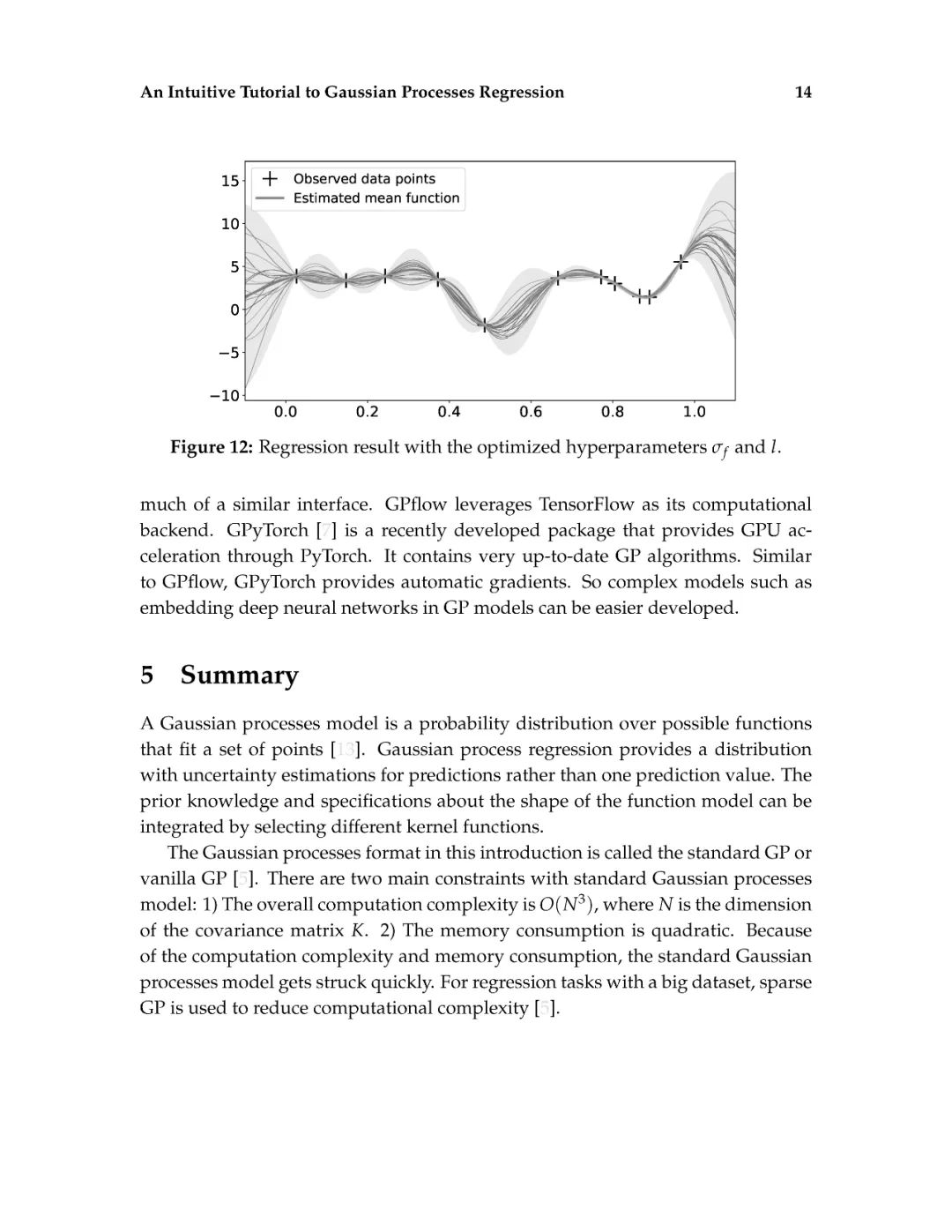
这篇介绍旨在为读者提供对高斯过程回归的直观理解。高斯过程回归(GPR)模型由于其表示法的灵活性和预测的固有不确定性，在机器学习应用中得到了广泛的应用。本文首先解释了高斯过程所建立的数学基础，包括多元正态分布、核、非参数模型、联合概率和条件概率。然后，通过显示不必要的数学推导步骤和缺少关键的结论性结果的平衡，以可访问的方式描述高斯过程回归。给出了一个标准高斯过程回归算法的说明性实现。除了标准的高斯过程回归之外，现有的软件包实现了最先进的高斯过程算法。最后，给出了更高级的高斯过程回归模型。这篇论文的写作方式通俗易懂，理工科本科学生理解文章内容不会有困难。

https://arxiv.org/abs/2009.10862

专知便捷查看

便捷下载，请关注专知公众号（点击上方蓝色专知关注）

• 后台回复“GP19” 可以获取《最新《高斯过程回归简明教程》，19页pdf》专知下载链接索引

专知，专业可信的人工智能知识分发，让认知协作更快更好！欢迎注册登录专知www.zhuanzhi.ai，获取5000+AI主题干货知识资料！

欢迎微信扫一扫加入专知人工智能知识星球群，获取最新AI专业干货知识教程资料和与专家交流咨询！

点击“ 阅读原文 ”，了解使用 专知 ，查看获取5000+AI主题知识资源